Available on Google PlayApp Store

何分の

jeanne6663
なにぶんの

Meaning

何分の なにぶんの
noun (common) (futsuumeishi)
  • some
  • something or other
  • as much as possible

Kanji

  • 何
  • 分
    • onyomiブン ・ フン ・ ブ
    • kunyomiわ.ける ・ わ.け ・ わ.かれる ・ わ.かる ・ わ.かつ
    • meaningpart; minute of time; segment; share; degree; one's lot; duty; understand; know; rate; 1%; chances; shaku/100
      • Print WorksheetDictionary

Sentences

  • Japanese 彼は１秒のほんの何分の１かでそれをした。
    English He did it in only a fraction of a second.
  • Japanese 「64GBのUSBメモリが16ユーロで買えるとかすごい時代だなあ」「これがまた10年後には何分の一かの値段になってるんだろうね」

Shopping

Images

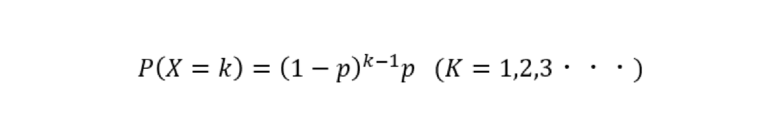
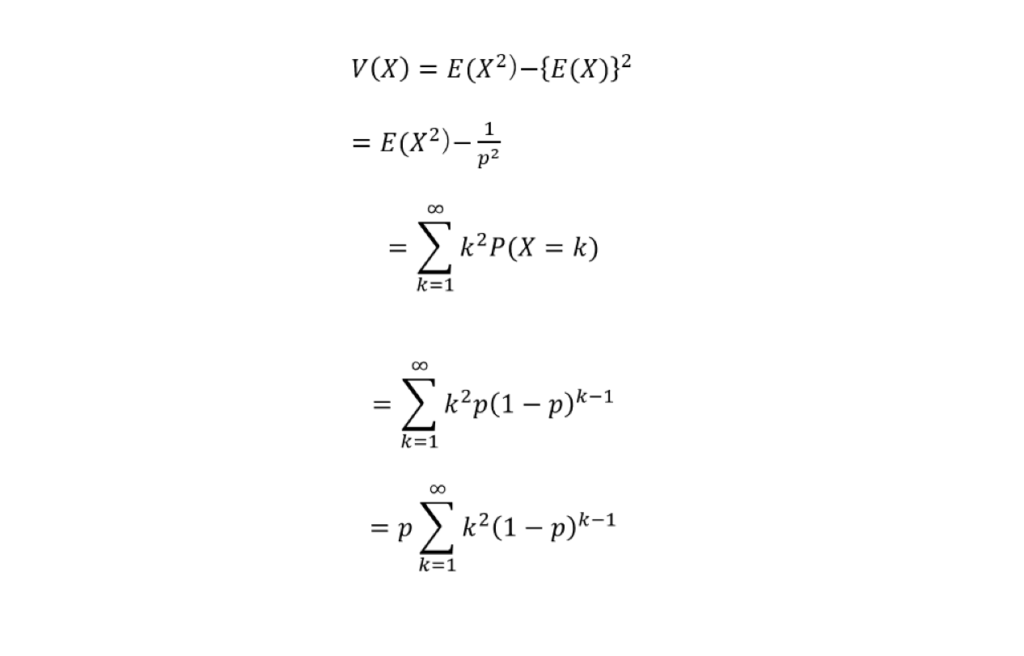
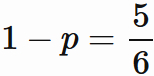
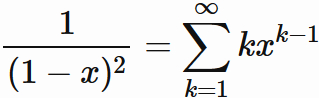
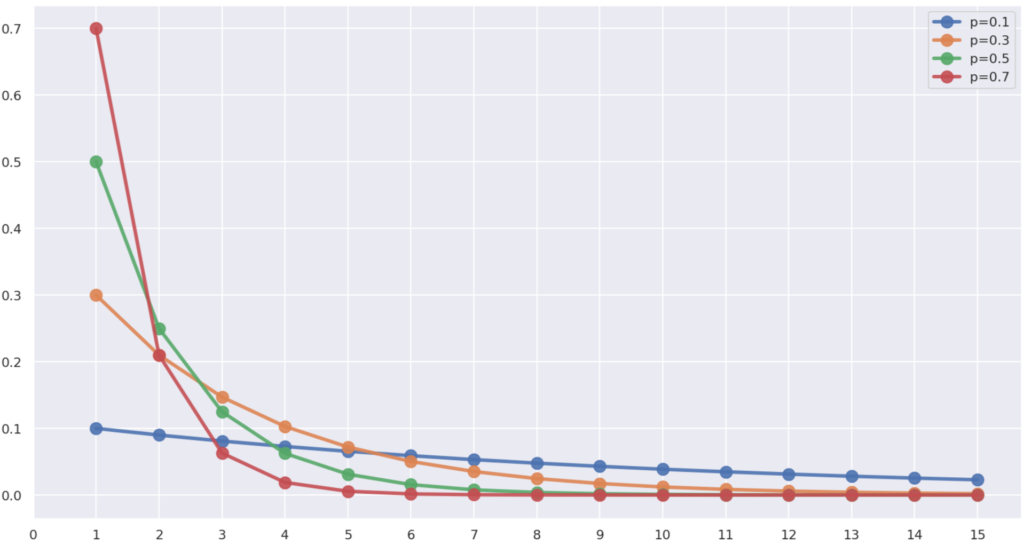
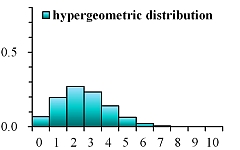
幾何分布とは？期待値（平均）や分散の証明はどうなるか例題を用いて解説Juliaで学ぶ確率変数(3) - 幾何分布（離散型）１．幾何分布 Ge(p)幾何分布の期待値(平均)・分散・標準偏差とその導出証明デミング博士のニューエコノミクスって反比例っぽいグラフはどのようにして生まれるのか？前略反比例のグラフ草々幾何分布の定義と性質まとめ幾何分布の定義と性質まとめ幾何分布の母数推定における予測推定量幾何分布とは？期待値（平均）や分散の証明はどうなるか例題を用いて解説幾何分布幾何分布p=0.1,0.3,0.5,0.7と変えたときの，幾何分布の確率(質量)関数の違い集客に繋がる福岡市のホームページ制作会社アライブキャスト スタッフブログ STAFF BLOG 様々な確率分布天井付きガシャの期待値（上限付き？幾何分布）について幾何分布f:id:yanbow221:20170902095612p:plain幾何分布とは？期待値（平均）や分散の証明はどうなるか例題を用いて解説幾何分布とは？期待値（平均）や分散の証明はどうなるか例題を用いて解説\begin{eqnarray*} P(X=k)=(1-p)^{k-1} p & (k=1,2,3,\cdots) \\ \end{eqnarray*}f:id:ganbaru_engineer:20190806002214p:plain幾何分布【統計検定準１級のための数学①】超幾何分布幾何分布の具体例と期待値，無記憶性について\begin{eqnarray*} \displaystyle E[X^2]-(1-p)E[X^2] &=& pE[X^2] \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - (1-p)\sum_{x=0}^n (2x+1)(1-p)^{x} \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - \sum_{x=0}^n (2x+1)(1-p)^{x+1} \\ &=& \left\{ 1 \times (1-p)^{0} + 3 \times (1-p)^{1} + 5 \times (1-p)^{2} + \dots \right\} \\ && - \left\{ 1 \times (1-p)^{1} + 3 \times (1-p)^{2} + 5 \times (1-p)^{3} + \dots \right\} \\ &=& \left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 2 \times (1-p)^{2} + \dots \right\} \\ &=& 1 + 2 \times \sum_{x=1}^n (1-p)^{x} \\ \end{eqnarray*}13-7. 超幾何分布練習問題 : モンテカルロ統計計算 Chapter 5 ギブスサンプリング負の超幾何分布とは？ わかりやすく解説ハンドルームコットンカディー マルチクロ...のレビュー・口コミ統計検定２級に最短で合格する方法【チートシート有り】超幾何分布超幾何分布 (hypergeometric distribution)ざっくりした説明二項分布との関係確率分布であることの確認期待値の導出分散の導出参考\begin{eqnarray*} \displaystyle M''_X(t) &=& \frac{pe^t\{1-e^t(1-p)\}^2+pe^t \times 2\{1-e^t(1-p)\} \times e^t(1-p)}{\{1-e^t(1-p)\}^4} \end{eqnarray*}2変量正規分布の幾何学的解釈幾何分布とは？期待値（平均）や分散の証明はどうなるか例題を用いて解説f:id:nishiru3:20180612225718p:plainMENUBASIC STUDYPROGRAMMINGAI REPORTABOUT USAVILEN片側検定と両側検定の違いをわかりやすく解説超幾何分布について｜Excel（エクセル）で学ぶデータ分析ブログ
View more

Share