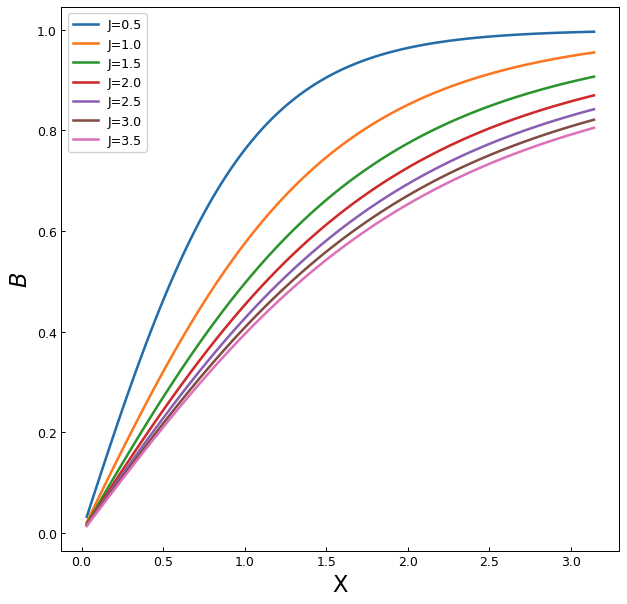
Images of ブリルアン関数とランジュバン関数
![\begin{eqnarray*}B_J(x)&=&\frac{1}{3}\Bigl( \frac{2J+1}{2J} \Bigr)^2 \,x -\frac{1}{3}\Bigl( \frac{1}{2J} \Bigr)^2 \,x + O(x^3) \\ \\&=&\frac{1}{3}\Bigl[ \left( \frac{2J+1}{2J} \right)^2 - \left( \frac{1}{2J} \right)^2 \Bigr] + O(x^3) \\ \\&=&\frac{1}{3}\, \left( \frac{1}{2J}\right)^2 \Bigl[ (2J+1)^2 - 1 \Bigr]+ O(x^3) \\ \\&=&\frac{1}{3}\, \frac{1}{4J^2} \, (4J^2 + 4J) + O(x^3) \\ \\&=&\frac{1}{3}\, \frac{1}{4J^2} \, 4J(J+1) + O(x^3) \\ \\&=&\frac{J+1}{3J}+O(x^3)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-bc5bfc333b49ebde6b594f9a2509704a_l3.png)
\begin{eqnarray*}B_J(x)&=&\frac{1}{3}\Bigl( \frac{2J+1}{2J} \Bigr)^2 \,x -\frac{1}{3}\Bigl( \frac{1}{2J} \Bigr)^2 \,x + O(x^3) \\ \\&=&\frac{1}{3}\Bigl[ \left( \frac{2J+1}{2J} \right)^2 - \left( \frac{1}{2J} \right)^2 \Bigr] + O(x^3) \\ \\&=&\frac{1}{3}\, \left( \frac{1}{2J}\right)^2 \Bigl[ (2J+1)^2 - 1 \Bigr]+ O(x^3) \\ \\&=&\frac{1}{3}\, \frac{1}{4J^2} \, (4J^2 + 4J) + O(x^3) \\ \\&=&\frac{1}{3}\, \frac{1}{4J^2} \, 4J(J+1) + O(x^3) \\ \\&=&\frac{J+1}{3J}+O(x^3)\end{eqnarray*}
![\begin{eqnarray*} M&=&Ng\mu_B J\frac{d}{dx}\ln{\left[ \textcolor{red}{\sum_{J_z=-J}^{J} \exp{\left(-\frac{xJ_z}{J}\right)} }\right]}\\\\\\ &=& Ng\mu_B J\frac{d}{dx}\ln{\left[ \textcolor{red}{ \frac{\sinh{\left(\frac{2J+1}{2J}x\right)}}{\sinh{\left(\frac{x}{2J}\right)}} }\right]}\\\\\\ &=& Ng\mu_B J\left\{ \frac{d}{dx}\ln{\left[ \sinh{\left(\frac{2J+1}{2J}x\right)}}\right]} -\frac{d}{dx}\ln{\left[ \sinh{\left(\frac{x}{2J}\right)} }\right] \right\}\\\\\\ &=& Ng\mu_B J\left[ \frac{2J+1}{2J}\coth{\left(\frac{2J+1}{2J}x\right)}} - \frac{1}{2J}\coth{\left(\frac{x}{2J}\right)} \right]\\\\\\ &=& Ng\mu_B J B_J(x) \quad \blacksquare \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-8c54d40eb626994901ec8c2eb60edeb8_l3.png)
\begin{eqnarray*} M&=&Ng\mu_B J\frac{d}{dx}\ln{\left[ \textcolor{red}{\sum_{J_z=-J}^{J} \exp{\left(-\frac{xJ_z}{J}\right)} }\right]}\\\\\\ &=& Ng\mu_B J\frac{d}{dx}\ln{\left[ \textcolor{red}{ \frac{\sinh{\left(\frac{2J+1}{2J}x\right)}}{\sinh{\left(\frac{x}{2J}\right)}} }\right]}\\\\\\ &=& Ng\mu_B J\left\{ \frac{d}{dx}\ln{\left[ \sinh{\left(\frac{2J+1}{2J}x\right)}}\right]} -\frac{d}{dx}\ln{\left[ \sinh{\left(\frac{x}{2J}\right)} }\right] \right\}\\\\\\ &=& Ng\mu_B J\left[ \frac{2J+1}{2J}\coth{\left(\frac{2J+1}{2J}x\right)}} - \frac{1}{2J}\coth{\left(\frac{x}{2J}\right)} \right]\\\\\\ &=& Ng\mu_B J B_J(x) \quad \blacksquare \end{eqnarray*}
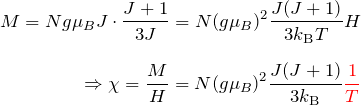
\begin{eqnarray*} M=Ng\mu_B J\cdot\frac{J+1}{3J}=N(g\mu_B)^2 \frac{J(J+1)}{3k_{\rm B}T}H\\\\ \Rightarrow \chi=\frac{M}{H}=N(g\mu_B)^2 \frac{J(J+1)}{3k_{\rm B}}\textcolor{red}{\frac{1}{T}} \end{eqnarray*}
![\begin{eqnarray*}&&\frac{1}{2J}{\rm coth}\left(\frac{1}{2J}x\right)\\ \\=&&\frac{1}{2J}\Bigl[ \frac{2J}{x} + \frac{1}{3}\,\frac{x}{2J}+O(x^3)\Bigr]\\ \\=&&\frac{1}{x}+\frac{1}{3}\Bigl( \frac{1}{2J} \Bigr)^2 \,x + O(x^3) \quad \cdots (2)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-007d8f75cd97670ac851ecdee02559d4_l3.png)
\begin{eqnarray*}&&\frac{1}{2J}{\rm coth}\left(\frac{1}{2J}x\right)\\ \\=&&\frac{1}{2J}\Bigl[ \frac{2J}{x} + \frac{1}{3}\,\frac{x}{2J}+O(x^3)\Bigr]\\ \\=&&\frac{1}{x}+\frac{1}{3}\Bigl( \frac{1}{2J} \Bigr)^2 \,x + O(x^3) \quad \cdots (2)\end{eqnarray*}
![\begin{eqnarray*} {\rm ln}(\sigma_1)&=& {\rm ln}(\sigma_0)-\frac{1}{2k_B T_1} \frac{2k_B T_1 T_2}{T_2 - T_1}\Bigl[ {\rm ln}(\sigma_2)-{\rm ln}(\sigma_1) \Bigr]\\ &=&{\rm ln}(\sigma_0) - \frac{T_2}{T_2 - T_1}\Bigl[ {\rm ln}(\sigma_2)-{\rm ln}(\sigma_1) \Bigr]\\ \leftrightarrow {\rm ln}(\sigma_0) &=& {\rm ln}(\sigma_1) + \frac{T_2}{T_2 - T_1}\Bigl[ {\rm ln}(\sigma_2)-{\rm ln}(\sigma_1) \Bigr]\\ &=& \frac{T_2 {\rm ln}(\sigma_2) -T_1 {\rm ln}(\sigma_1)}{T_2 - T_1} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-ae828d34f4f31a3e08a22f27d1a7c221_l3.png)
\begin{eqnarray*} {\rm ln}(\sigma_1)&=& {\rm ln}(\sigma_0)-\frac{1}{2k_B T_1} \frac{2k_B T_1 T_2}{T_2 - T_1}\Bigl[ {\rm ln}(\sigma_2)-{\rm ln}(\sigma_1) \Bigr]\\ &=&{\rm ln}(\sigma_0) - \frac{T_2}{T_2 - T_1}\Bigl[ {\rm ln}(\sigma_2)-{\rm ln}(\sigma_1) \Bigr]\\ \leftrightarrow {\rm ln}(\sigma_0) &=& {\rm ln}(\sigma_1) + \frac{T_2}{T_2 - T_1}\Bigl[ {\rm ln}(\sigma_2)-{\rm ln}(\sigma_1) \Bigr]\\ &=& \frac{T_2 {\rm ln}(\sigma_2) -T_1 {\rm ln}(\sigma_1)}{T_2 - T_1} \end{eqnarray*}






![OPI オーピーアイ ベースコート 15ml NTT10 国内正規品 O・P・I ベース・トップコート [0015/NTT10] メール便無料[A][TG100] ナチュラルネイル ベースコート マニキュア 保護](https://thumbnail.image.rakuten.co.jp/@0_mall/cosmenana/cabinet/10585/1058502015.jpg?_ex=300x300)



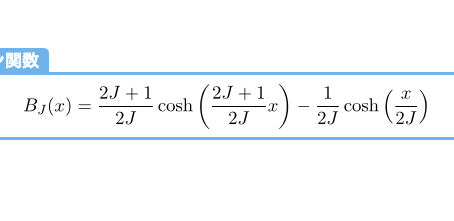




![【ポイント10倍】アンドネイル モイスチャースパリムーバーN(除光液) 100mL [石澤研究所 アンドネイル&nail]【北海道 宅配 3980〜9799円のご注文は自動キャンセル】](https://thumbnail.image.rakuten.co.jp/@0_mall/loco/cabinet/shohin-a/ishizawa/andnail/iz_nail_remover.jpg?_ex=300x300)




![\begin{eqnarray*}\lambda_0 &=& \frac{1.24}{100} \\ \\&=& 0.0124 \; {\rm [nm]}\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-acd6dead2000bd598ed7e080896f940f_l3.png)