Images of ベクトル解析の公式の一覧
Yahoo!知恵袋図形問題です。よろしくお願いします。 図のように半径3cmの2つの円が各々の円の中心を通って重なっています。 AからB、C、Dを通って、Aに戻るまでの長さはどれだけですか? (※中の交わっている部分以外の外周)
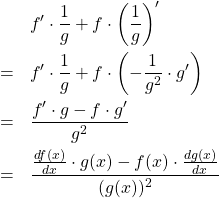
\begin{eqnarray*} && f' \cdot \frac{1}{g} + f \cdot \left( \frac{1}{g} \right)' \\ &=& f' \cdot \frac{1}{g} + f \cdot \left( - \frac{1}{g^2} \cdot g' } \right) \\ &=& \frac{ f' \cdot g - f \cdot g'}{g^2} \\ &=& \frac{ \frac{d f(x)}{dx} \cdot g(x) - f(x) \cdot \frac{d g(x)}{dx} }{(g(x))^2} \end{eqnarray*}
![\begin{eqnarray*} &&\nabla \cdot (\phi {\bf A}) \\ &=& \left( \frac{\partial }{\partial x }, \frac{\partial }{\partial y }, \frac{\partial}{\partial z } \right)\cdot (\phi {\bf A})\\ &=& \left( \frac{\partial }{\partial x }, \frac{\partial }{\partial y }, \frac{\partial}{\partial z } \right)\cdot \left( \phi A_x , \phi A_y , \phi A_z \right)\\ &=& \frac{\partial (\phi A_x)}{\partial x } + \frac{\partial (\phi A_y)}{\partial y } + \frac{\partial (\phi A_z)}{\partial z } \\ &=& \phi \frac{\partial A_x}{\partial x } + \frac{\partial \phi }{\partial x } A_x \\ && \quad + \phi \frac{\partial A_y}{\partial y } + \frac{\partial \phi }{\partial y } A_y \\ && \qquad + \phi \frac{\partial A_z}{\partial z } + \frac{\partial \phi }{\partial z } A_z \\ &=& \left( \phi \frac{\partial A_x}{\partial x } + \phi \frac{\partial A_y}{\partial y } + \phi \frac{\partial A_z}{\partial z } \right) \\ && \quad + \left( \frac{\partial \phi }{\partial x } A_x + \frac{\partial \phi }{\partial y } A_y + \frac{\partial \phi }{\partial z } A_z \right) \\ &=& \phi \left( \frac{\partial A_x}{\partial x } + \frac{\partial A_y}{\partial y } + \frac{\partial A_z}{\partial z } \right) \\ && \quad + \left( \frac{\partial \phi }{\partial x }, \frac{\partial \phi }{\partial y }, \frac{\partial \phi }{\partial z } \right) \cdot \left( A_x, A_y, A_z \right)\\ &=& \phi \left( \frac{\partial}{\partial x }, \frac{\partial}{\partial y }, \frac{\partial}{\partial z } \right) \cdot \left( A_x, A_y, A_z \right) \\ && \quad + \left[ \left( \frac{\partial}{\partial x }, \frac{\partial}{\partial y }, \frac{\partial}{\partial z } \right)\phi \right] \cdot \left( A_x, A_y, A_z \right)\\ &=& \phi (\nabla \cdot {\bf A}) + (\nabla \phi) \cdot {\bf A} \end{eqnarray*}](https://k-san.link/wp-content/ql-cache/quicklatex.com-c5ea188563f3211fcb0c82629703a3b8_l3.png)
\begin{eqnarray*} &&\nabla \cdot (\phi {\bf A}) \\ &=& \left( \frac{\partial }{\partial x }, \frac{\partial }{\partial y }, \frac{\partial}{\partial z } \right)\cdot (\phi {\bf A})\\ &=& \left( \frac{\partial }{\partial x }, \frac{\partial }{\partial y }, \frac{\partial}{\partial z } \right)\cdot \left( \phi A_x , \phi A_y , \phi A_z \right)\\ &=& \frac{\partial (\phi A_x)}{\partial x } + \frac{\partial (\phi A_y)}{\partial y } + \frac{\partial (\phi A_z)}{\partial z } \\ &=& \phi \frac{\partial A_x}{\partial x } + \frac{\partial \phi }{\partial x } A_x \\ && \quad + \phi \frac{\partial A_y}{\partial y } + \frac{\partial \phi }{\partial y } A_y \\ && \qquad + \phi \frac{\partial A_z}{\partial z } + \frac{\partial \phi }{\partial z } A_z \\ &=& \left( \phi \frac{\partial A_x}{\partial x } + \phi \frac{\partial A_y}{\partial y } + \phi \frac{\partial A_z}{\partial z } \right) \\ && \quad + \left( \frac{\partial \phi }{\partial x } A_x + \frac{\partial \phi }{\partial y } A_y + \frac{\partial \phi }{\partial z } A_z \right) \\ &=& \phi \left( \frac{\partial A_x}{\partial x } + \frac{\partial A_y}{\partial y } + \frac{\partial A_z}{\partial z } \right) \\ && \quad + \left( \frac{\partial \phi }{\partial x }, \frac{\partial \phi }{\partial y }, \frac{\partial \phi }{\partial z } \right) \cdot \left( A_x, A_y, A_z \right)\\ &=& \phi \left( \frac{\partial}{\partial x }, \frac{\partial}{\partial y }, \frac{\partial}{\partial z } \right) \cdot \left( A_x, A_y, A_z \right) \\ && \quad + \left[ \left( \frac{\partial}{\partial x }, \frac{\partial}{\partial y }, \frac{\partial}{\partial z } \right)\phi \right] \cdot \left( A_x, A_y, A_z \right)\\ &=& \phi (\nabla \cdot {\bf A}) + (\nabla \phi) \cdot {\bf A} \end{eqnarray*}
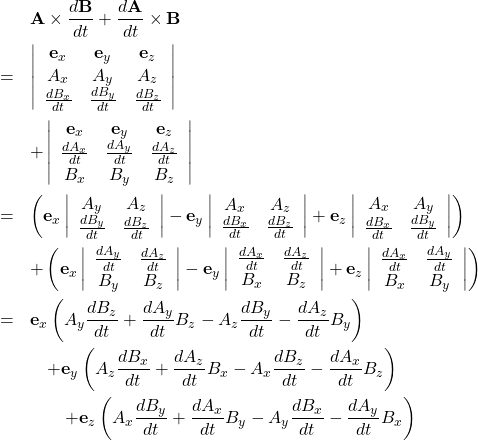
\begin{eqnarray*} && {\bf A} \times \frac{d {\bf B}}{dt} + \frac{d {\bf A} }{dt} \times {\bf B} \\ &=& \left| \begin{array}{ccc} {\bf e}_x & {\bf e}_y & {\bf e}_z\\ A_x & A_y & A_z\\ \frac{dB_x}{dt} & \frac{dB_y}{dt} & \frac{dB_z}{dt} \end{array} \right| \\ && + \left| \begin{array}{ccc} {\bf e}_x & {\bf e}_y & {\bf e}_z\\ \frac{dA_x}{dt} & \frac{dA_y}{dt} & \frac{dA_z}{dt} \\ B_x & B_y & B_z \end{array} \right| \\ &=& \left( {\bf e}_x \left| \begin{array}{cc} A_y & A_z\\ \frac{dB_y}{dt} & \frac{dB_z}{dt} \end{array} \right| - {\bf e}_y \left| \begin{array}{cc} A_x & A_z\\ \frac{dB_x}{dt} & \frac{dB_z}{dt} \end{array} \right| + {\bf e}_z \left| \begin{array}{cc} A_x & A_y \\ \frac{dB_x}{dt} & \frac{dB_y}{dt} \end{array} \right| \right)\\ &&+ \left( {\bf e}_x \left| \begin{array}{cc} \frac{dA_y}{dt} & \frac{dA_z}{dt} \\ B_y & B_z \end{array} \right| - {\bf e}_y \left| \begin{array}{cc} \frac{dA_x}{dt} & \frac{dA_z}{dt} \\ B_x & B_z \end{array} \right| + {\bf e}_z \left| \begin{array}{cc} \frac{dA_x}{dt} & \frac{dA_y}{dt} \\ B_x & B_y \end{array} \right| \right)\\ &=& {\bf e}_x \left( A_y \frac{dB_z}{dt} + \frac{dA_y}{dt} B_z - A_z \frac{dB_y}{dt} - \frac{dA_z}{dt} B_y \right)\\ &&\quad +{\bf e}_y \left( A_z \frac{dB_x}{dt} + \frac{dA_z}{dt} B_x - A_x \frac{dB_z}{dt} - \frac{dA_x}{dt} B_z \right)\\ &&\qquad +{\bf e}_z \left( A_x \frac{dB_y}{dt} + \frac{dA_x}{dt} B_y - A_y \frac{dB_x}{dt} - \frac{dA_y}{dt} B_x \right) \end{eqnarray*}























![[美容をトータルサポート♪]ナウフーズ ビオチン サプリメント 5000mcg 120粒 NOW Foods Biotin ベジカプセル ビタミンH 120日分 単品 セット](https://thumbnail.image.rakuten.co.jp/@0_mall/harmony/cabinet/item/n_01/nf-00474.jpg?_ex=300x300)