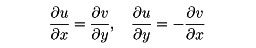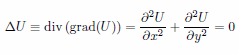
Sample Scripts from GB Books ラプラス方程式、ポアッソン方程式

【1500円OFFクーポン有】セクシーランジェリー 超過激 穴あき 大きいサイズ セクシー ランジェリー 過激 ベビードール セクシー下着 エロ下着 ランジェリー ルームウェア 股割れ XL 2L…

【1500円OFFクーポン有】ストッキング タイツ セクシーランジェリー ガーターベルト 大きいサイズ XL 3L 4L 超過激 セクシー ニーハイ 7分丈 ストッキング 伸縮性 幅広レース…

【1500円OFFクーポン有】セクシーランジェリー 大きいサイズ セクシーランジェリー 過激 セクシーランジェリー ベビードール セクシー下着 エロ下着 ランジェリー ベビードールランジェリー…
![\begin{eqnarray*} &&{\mathcal L}\left[y(t)\right]={\mathcal L}\left[t\right](s)+{\mathcal L}\left[\int_0^{t}y(\tau)d\tau\right]\\\\ \Leftrightarrow&&Y(s)=\frac{1}{s^2}+\frac{Y(s)}{s}\\\\ \Leftrightarrow&& Y(s)=\frac{1}{s(s-1)}=\frac{1}{s-1}-\frac{1}{s} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-fa89d36352d7344e0d1afd4f6fc9fd9a_l3.png)
\begin{eqnarray*} &&{\mathcal L}\left[y(t)\right]={\mathcal L}\left[t\right](s)+{\mathcal L}\left[\int_0^{t}y(\tau)d\tau\right]\\\\ \Leftrightarrow&&Y(s)=\frac{1}{s^2}+\frac{Y(s)}{s}\\\\ \Leftrightarrow&& Y(s)=\frac{1}{s(s-1)}=\frac{1}{s-1}-\frac{1}{s} \end{eqnarray*}

ブラ ショーツ セット 丸見えブラ 「S M Lサイズ丸見え悩殺SEXYフルバスト オープンブラ & 穴あきショーツセット お花のレース」セクシー ランジェリー 下着 ハーフカップ オープンバスト…

セクシー ランジェリー ブラ ショーツ セット オープン 穴あき エロ 下着 過激 マンホールブラ ノンワイヤーブラ セクシーランジェリ セクシ-ランジェリー 超過激 紐 大人 女性 レディース…
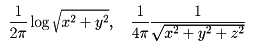
ラプラス方程式(読み)らぷらすほうていしき(英語表記)Laplace's equation

【10%OFF】【1500円OFFクーポン有】マイクロビキニ マイクロ ビキニ セクシーランジェリー 超過激 セクシービキニ 極小ビキニ セクシー コスプレ セクシーランジェリー 水着 セクシー…

【京都】鳥獣戯画で有名な『高山寺』へ!青もみじや苔を見て楽しんできました!
![\begin{eqnarray*} {\mathcal L}[f(t-t_0)]= \begin{cases} e^{-st_0} {\mathcal L}[f(t)]\quad(t\geq t_0)\\\\ 0\quad(t](https://batapara.com/wp-content/ql-cache/quicklatex.com-dab6a1c8de019063143890f36f85f371_l3.png)
\begin{eqnarray*} {\mathcal L}[f(t-t_0)]= \begin{cases} e^{-st_0} {\mathcal L}[f(t)]\quad(t\geq t_0)\\\\ 0\quad(t

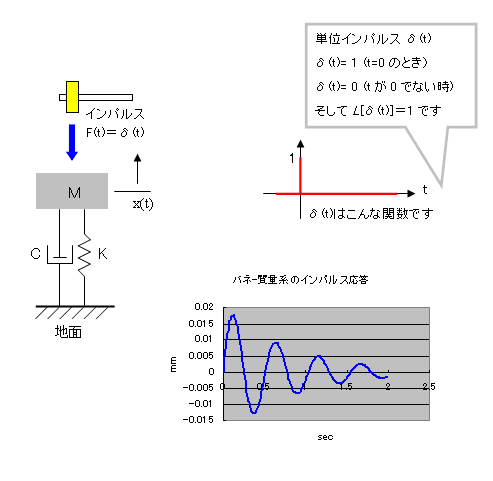
tswat's blog 2階非斉次微分方程式を、ラプラス変換で解く。

スリップ サテン プチプラ 透けない セクシー ランジェリー ベビードール 大きいサイズ 光沢 上品 エレガント かわいい スリット リボン タイト 勝負下着 su960 プレゼント ギフト…
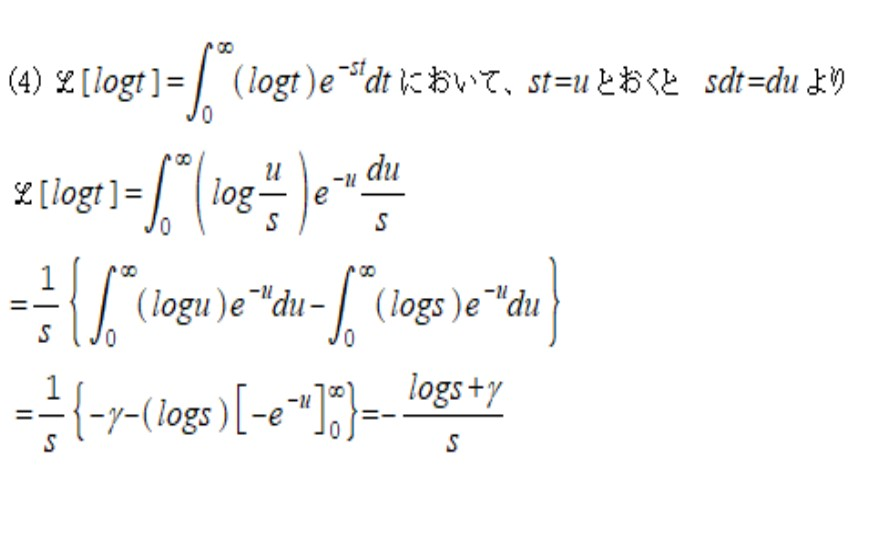
Yahoo!知恵袋次のラプラス変換と積分方程式の問題がわかりません。どなたか教えてください!
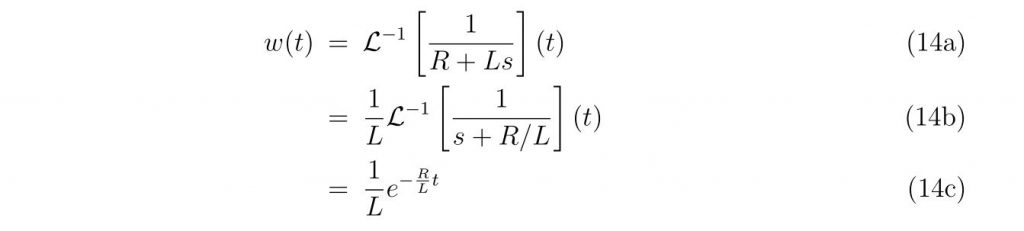
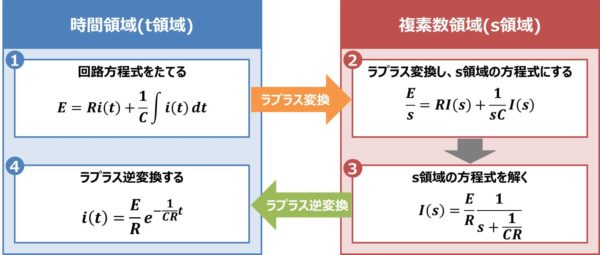
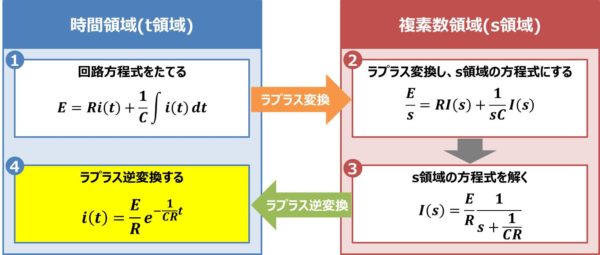
シキノートラプラス変換による回路方程式の解 投稿ナビゲーション 人気のページPSO2のスクリーンショット= カタログ =スポンサーリンク※トップ絵ライセンスメタ情報アーカイブ最近のコメント

物理、方程式、黒板、式、シュレディンガー方程式、ラプラス演算子、量子物理学、量子力学、理論物理学、チョーク、教育

【1500円OFFクーポン有】セクシーランジェリー 大きいサイズ ブラ ショーツ 穴あき オープンブラ XL 3L 4L 超過激 セクシーランジェリー セクシー下着 エロ下着 ランジェリー…

【バーゲン 23%OFF】ブラジャー ショーツ セット 盛り Lace ソフト超盛ブラ(R) ブラジャー&ショーツ (女性 下着 レディース ブラショーツ 小胸 超盛ブラ 盛りブラ 谷間…

Yahoo!知恵袋4次の部分分数分解について
ラプラス変換で微分方程式を解く問題で
詰まってしまいました
(as^3+bs^2+(4a+1)s+4b)/(s^2+4)^2

福C【バーゲン 特別価格】セクシー ショーツ スタンダード カシュクールレース プレーンショーツ(下着 パンティ パンツ かわいい パンティー 女性 レディース かわいい下着 可愛いショーツ 単品…
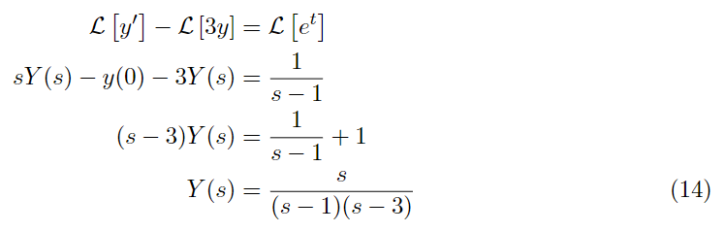
ディジタルローパスフィルタの設計をしてみる その6 ラプラス変換を用いて微分方程式を解く

ディジタルローパスフィルタの設計をしてみる その6 ラプラス変換を用いて微分方程式を解く

【1500円OFFクーポン有】セクシーランジェリー 大きいサイズ ベビードール 超過激 XL 3Lレディース セクシー ランジェリー 下着 セクシー 大きいサイズ セクシー コスチューム セクシー…

亀山尚輝の日記 現在ではラプラス方程式と呼ばれる方程式 ∆f = 0 の解は調和函数と呼ばれ、自由空間において可能な重力場を表現するものである。ラプラス作用素は、合同変換に対して不変な微分演算子の中で、自明なもの(=恒等的に0を対応させる微分演算子)を除けば最も簡単なものである。ラプラス作用素それ自身は拡散方程式によって記述されるような、科学密度の流入や漏出を表す点を含む非平衡拡散に対する物理的解釈を持つ。

【最大50%OFFクーポンあり!3日まで】 レオタード ハイレグ セクシーランジェリー オープンクロッチ 透け透け エッチな下着 エロ下着 勝負下着 コスプレ 彼女 可愛い 過激 超過激 エロ下着…
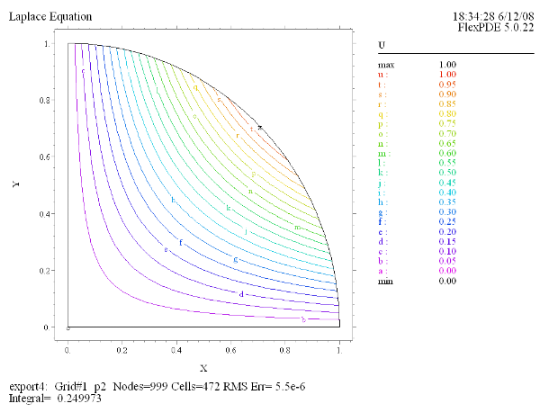
Sample Scripts from GB Books ラプラス方程式、ポアッソン方程式
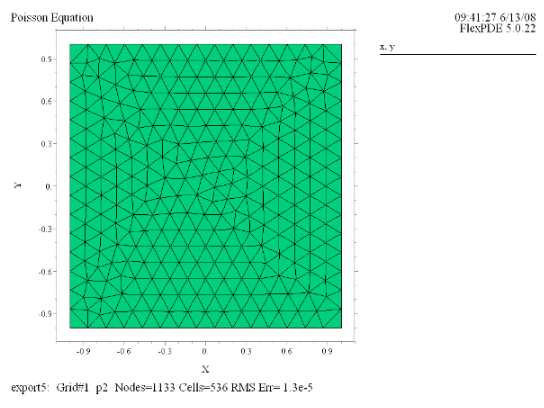
Sample Scripts from GB Books ラプラス方程式、ポアッソン方程式

【バーゲン 21%OFF】ブラジャー ショーツ セット サテン カシュクールレース脇高ブラ(R) ブラジャー&ショーツ(下着 レディース ブラ 女性 脇肉 ブラセット ブラショーツ 谷間…
![\begin{eqnarray*} &&{\mathcal L}\left[y(t)\right]={\mathcal L}\left[t\right](s)+{\mathcal L}\left[\int_0^{t}y(\tau)d\tau\right]\\\\ \Leftrightarrow&&Y(s)=\frac{1}{s^2}+\frac{Y(s)}{s}\\\\ \Leftrightarrow&& Y(s)=\frac{1}{s(s-1)}=\frac{1}{s-1}-\frac{1}{s} \end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-fa89d36352d7344e0d1afd4f6fc9fd9a_l3.png)
![\begin{eqnarray*} {\mathcal L}[f(t-t_0)]= \begin{cases} e^{-st_0} {\mathcal L}[f(t)]\quad(t\geq t_0)\\\\ 0\quad(t](https://batapara.com/wp-content/ql-cache/quicklatex.com-dab6a1c8de019063143890f36f85f371_l3.png)

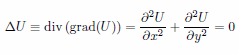


![方程式Tシャツ: ラプラス方程式(メンズ)[T-1-M]](https://media-01.creema.net/user/1222874/exhibits/2742946/0_fbbfb6da753ef9d2c67236b641fa2b65_583x585.jpg)










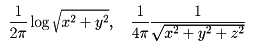




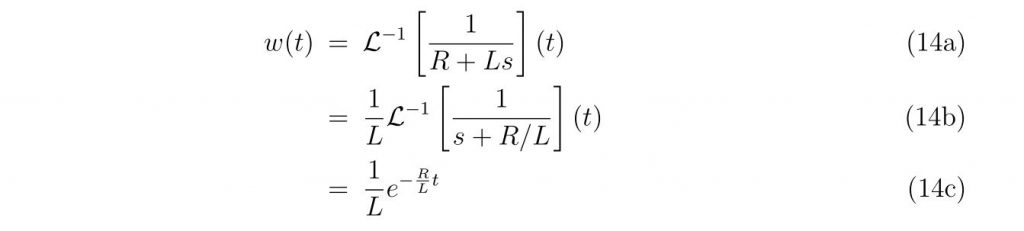







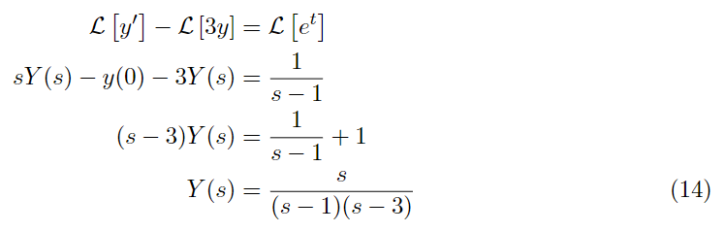








![[学习心得]---浅谈一阶非齐次线性常微分方程的特解——积分因子法](https://pic1.zhimg.com/v2-d1fc318dec7599db57faa0efaa7359da_r.jpg)