Images of リー微分

二階線形常微分方程式の非斉次の問題について教えてください。 view page

【中古】 コーエンの微分方程式 POD版-リー群論の応用view page

微分・積分回路 view page

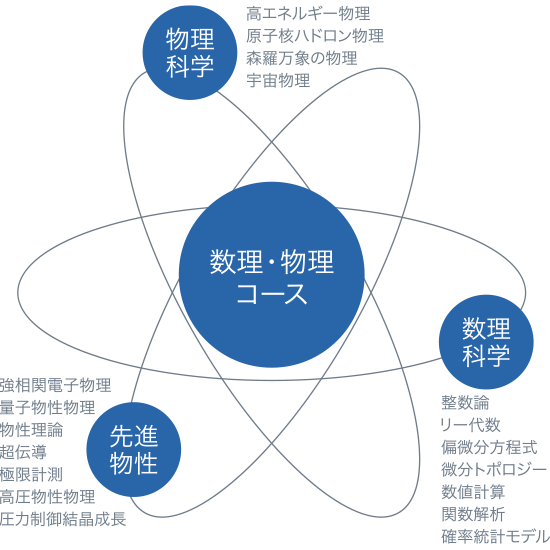
物理ノート 物理のためのリー群とリー代数序論連続変換群線形リー群とそのリー代数単純リー代数の分類３次元空間の回転と角運動量回転群の表現既約表現の分類群上の積分ハドロンの分類ゲージ相互作用の統一的記述ローレンツ群 view page

求z=In(xy)+e^(x+y^2)的全微分求z=In(xy)+e^(x+y^2)的全微分 view page

【未使用】【中古】 コーエンの微分方程式 POD版-リー群論の応用view page

「政策」が必ず失敗する原理 view page

https://cdn-ak.f.st-hatena.com/images/fotolife/c/cat_falcon/20190806/20190806021056.jpg view page

f:id:hiroki_f:20090405104840j:image view page

【中古】 コーエンの微分方程式 POD版-リー群論の応用view page

微分回路の式 view page

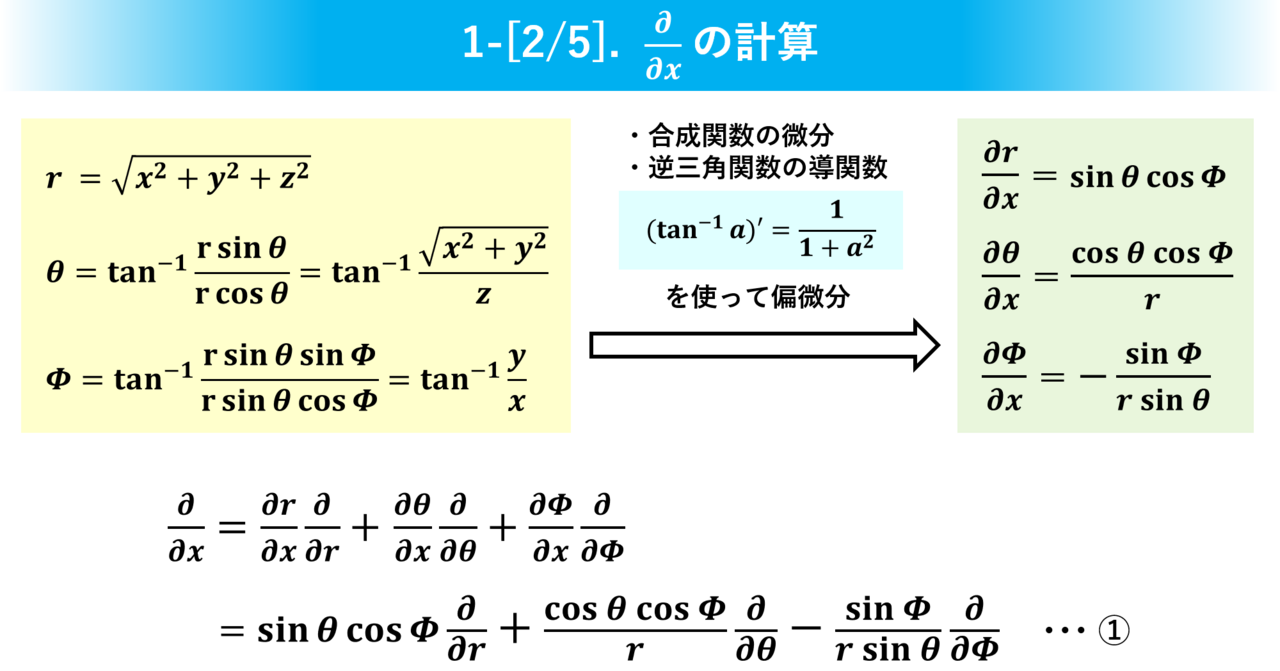
【量子化学】シュレディンガー方程式の微分演算子（∇^2）の偏微分計算をできるだけ分かりやすくまとめてみた view page

f:id:karia68:20181004181918j:plain view page

【中古-非常に良い】 コーエンの微分方程式 POD版-リー群論の応用view page

微分の基礎¶ view page

JavaScript is not available. view page

JavaScript is not available. view page

【中古】コーエンの微分方程式 POD版-リー群論の応用view page

退職教授の見果てぬ夢 view page

だれでもわかる微分方程式 view page

微分積分の超初心者に「5時間で攻略する本」レビュー view page

【中古】 コーエンの微分方程式 POD版-リー群論の応用view page

数理・物理コース view page

f:id:hiroki_f:20090406233253j:image view page

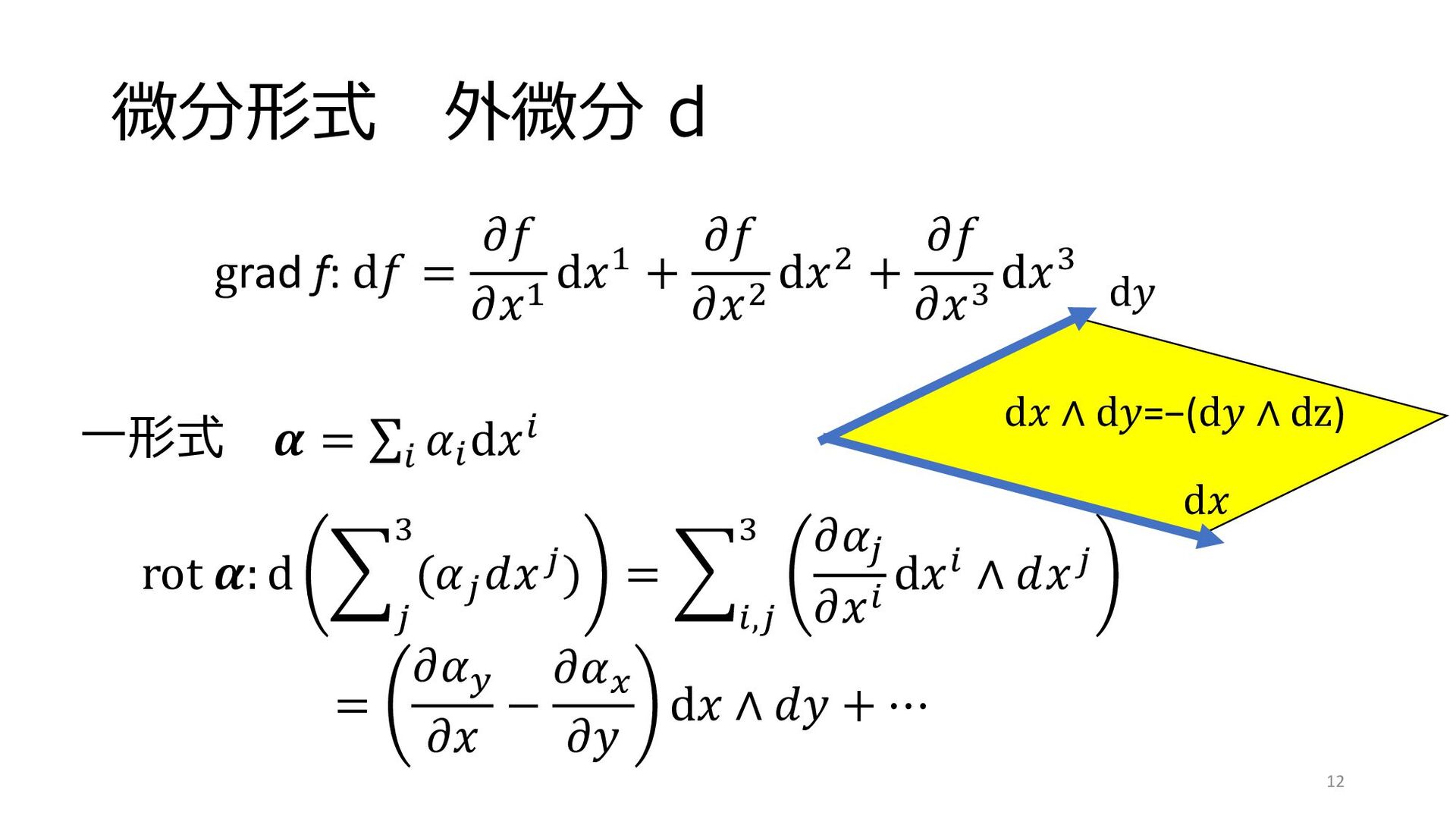
(新) 檜山正幸のキマイラ飼育記 メモ編 測度的微分形式＝測度形式 の過去記事と用語 view page

【中古】コーエンの微分方程式 POD版-リー群論の応用view page

リー微分、多様体の基礎 view page

長文失礼します。大学1年生(一般教養)です。勉強してみたいものが多すぎて、どこから手を付けるかや、どうやって勉強量を配分するかが分かりません。素人なので間違った例かもしれませんが、「解析力学には微分幾何や変分法が関係して、さらにそれはリー代数や関数解析にも絡むらしい」「量子といっても、量子情報や場の量子論もある…じゃあ情報数学や相対論も学んでみようかな」「流行りの機械学習や非線形数学もやりたい」など、面白そうな分野があると、それに関係したものも面白く見えたりして、実力は無いくせに色々と目移りしてしまいます(そのせいで、りょうに圧倒されてしまい何もできてない感触です)。当然それら全てを一気に学んでいくのは無理なのですが、勉強する対象をどうやって絞ればいいでしょう？また、学ぶものを絞った後の勉強の配分量、進め方も知りたいです。(例えば、複数分野を並行して進めていくか、又はまず数週間は特定の分野メインで進め、ある程度身に付いたら他のにシフトするか等)長く読みにくい文ですみませんが、宜しくお願いします。 view page

多様体上のリー微分と接続の共通点と相違点 view page

【中古】偏微分方程式 科学者・技術者のための使い方と解き方/ワイリ-・ジャパン/スタンリ-・J．ファ-ロウ（ペーパーバック）view page

D【参考書5】『リー代数』●東郷重明著●全253Ｐ●1983年刊●槙書店発行●検)微分/ルート/空間/幾何学/解析/定理/構造の1番目の画像 view page

sin2xの微分 view page

新着情報 教育研究シーズ（土木工学系　井上 公人） view page

リー群と表現論 view page

微分積分リアル入門 view page

Yahoo!知恵袋arctanxの3回微分が、何回やっても答えと合いません(>_<) どなたか途中式も加えて回答してください(･ω･) view page

微分方程式Differential Equation view page

f:id:tsujimotter:20200822012853p:plain:w240 view page

みどりぼん3章前半みどりぼん3章前半 view page

Yahoo!知恵袋logの微分で底がxのとき view page

回転座標系での古典場の方程式について。微分形式からの導出 view page

在这里插入图片描述 view page

偏微分とは?全微分/合成関数の微分と合わせてわかりやすく解説 view page

微分法（数学Ⅲ）の計算公式一覧【微分計算（数学Ⅲ）をマスターしよう】 view page

数学、微分記号について view page

在这里插入图片描述 view page