Images of 同型写像

JavaScript is not available. view page

【 特別 送料無料 】 1本たったの598円(税込) 3大銘醸地入り 世界選りすぐり赤ワイン11本セット 第276弾【7784807】 | 金賞 飲み比べ ワイン ワインセット wine…view page

Yahoo!知恵袋（3+2i）^2+（2-3i）=9+12i+4i^2+2-3iについて view page

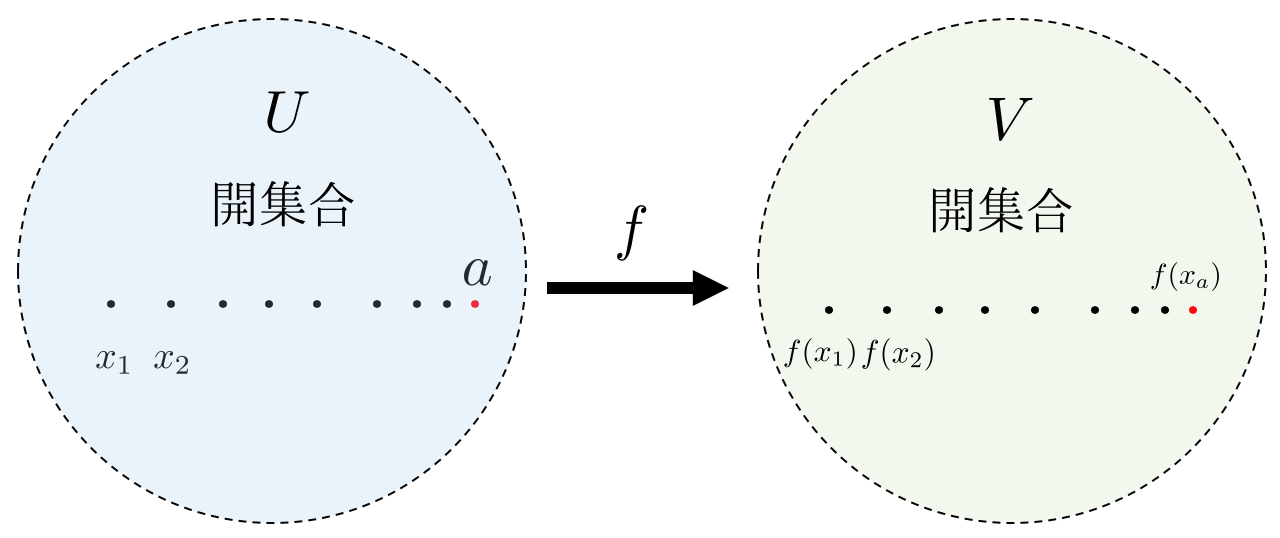
【今度こそわかる】同相写像とは（定義・性質）【今度こそわかる】同相写像とは（定義・性質） view page

商集合、同値関係・同値類を解説～商群の理解に向けて view page

アサヒ スーパードライ 缶( 350ml×24本入)【2shdrk】【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]view page

素数の分解法則（フロベニウスやばい） #math_cafe 素数の分解法則（フロベニウスやばい） #math_cafe view page

自己同型群の性質 view page

三浦と窮理とブログ 「準同型写像 f が単射である」ことと「 Ker f = {0} 」は同値であることの証明f は単射 ⇒ Ker f = {0} の証明Ker f = {0} ⇒ f は単射 の証明 view page

【 送料無料 】 1本あたり749円(税込) 格上メドック＆5冠金賞入り!フランス金賞赤ワイン12本セット 第105弾【7784110】 | 金賞受賞 飲み比べ ワイン ワインセット wine…view page

Yahoo!知恵袋【代数学】 view page

「第二同型定理の証明」重要な定理です！【代数学の基礎シリーズ】群論編 その7 view page

5．準同型写像，準同型定理 view page

＼18・19・20日は感謝デー全品★P3倍／ お歳暮 ビール ギフト セット 2025【本州のみ 送料無料】アサヒ AS-3N 『GIFT』スーパードライ 詰め合わせ 内祝い 誕生日 プレゼント…view page

準同型写像準同型単準同型，全準同型，同型準同型写像の核 view page

群論入門⑧(準同型写像) view page

【今度こそわかる】同相写像とは（定義・性質）【今度こそわかる】同相写像とは（定義・性質） view page

サントリー ザ・プレミアム・モルツ 26年干支デザイン午歳(350ml×24本)【ザ・プレミアム・モルツ(プレモル)】view page

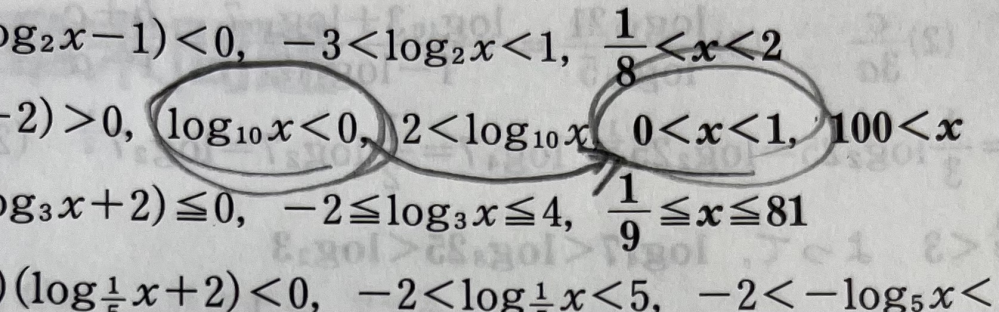
Yahoo!知恵袋Rを可換環、M,NをR-可群、φ:M→NをR-準同型写像とするとき、ImgφはNのR-部分加群であることを示してください。 view page

Yahoo!知恵袋大学数学です。 view page

自己同型群の性質 view page

【送料無料】世界選りすぐりスパークリングワイン11本セット 第40弾 スパークリングワイン 辛口 ワインセット 【7787498】view page

電気磁気工学を学ぶ view page

群論入門⑨(準同型定理) view page

群の同型写像 view page

【クリスマスくじ 第125弾】【150セット限定】激レアウイスキー入手困難なウイスキーを当てよう山崎18年 白州18年 山崎12年 白州12年 白州2024 2025 山崎2024 2025…view page

準同型写像のイメージ view page

吾輩の備忘録1. ベクトルと双対ベクトルの対応について2. pベクトルにおける双対基底の定義3. pベクトルのその双対ベクトルの対応4. p=0の場合 view page

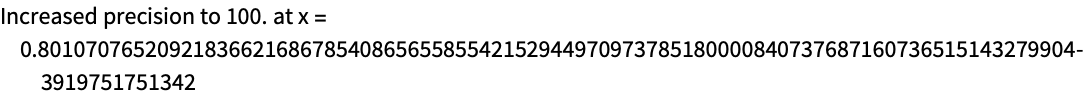
FindRoot詳細とオプション例題関連項目テクニカルノート関連するガイド関連リンクHistory view page

お歳暮 御歳暮 冬ギフト ビール お酒 プレゼント 2025 飲み比べ 詰め合わせ【送料無料】アサヒスーパードライ AS-5N 1セット SGL御礼 御祝 内祝 お誕生日 贈り物 高級 御年賀 お年賀view page

ATPとCASのこと A comparison of splitting field calculators view page

対角化とは？ view page

環準同型写像の定義 view page

アサヒ スーパードライ 缶(500ml*24本入)【2shdrk】【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]view page

AVX2時代の正規表現マッチング 〜半群でぐんぐん！〜 view page

[AtCoder 参加感想] 2020/03/21:AGC043 view page

線形写像の概要 view page

アサヒ スーパードライ 缶(350ml*48本セット)【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]view page

Yahoo!知恵袋環準同型写像に関する質問です。 view page

Haskellの代数的構造入門半群・モノイド・環とは何か？ view page

概要参加費用これまでの開催お問い合わせ view page

【抽選で1等77,777ポイント当たる！】お歳暮 御歳暮 冬ギフト ビール お酒 プレゼント 2025 飲み比べ 詰め合わせ【送料無料】サッポロ エビス 4種の味わいセット YNF3D 1セット…view page

準同型写像準同型単準同型，全準同型，同型準同型写像の核 view page

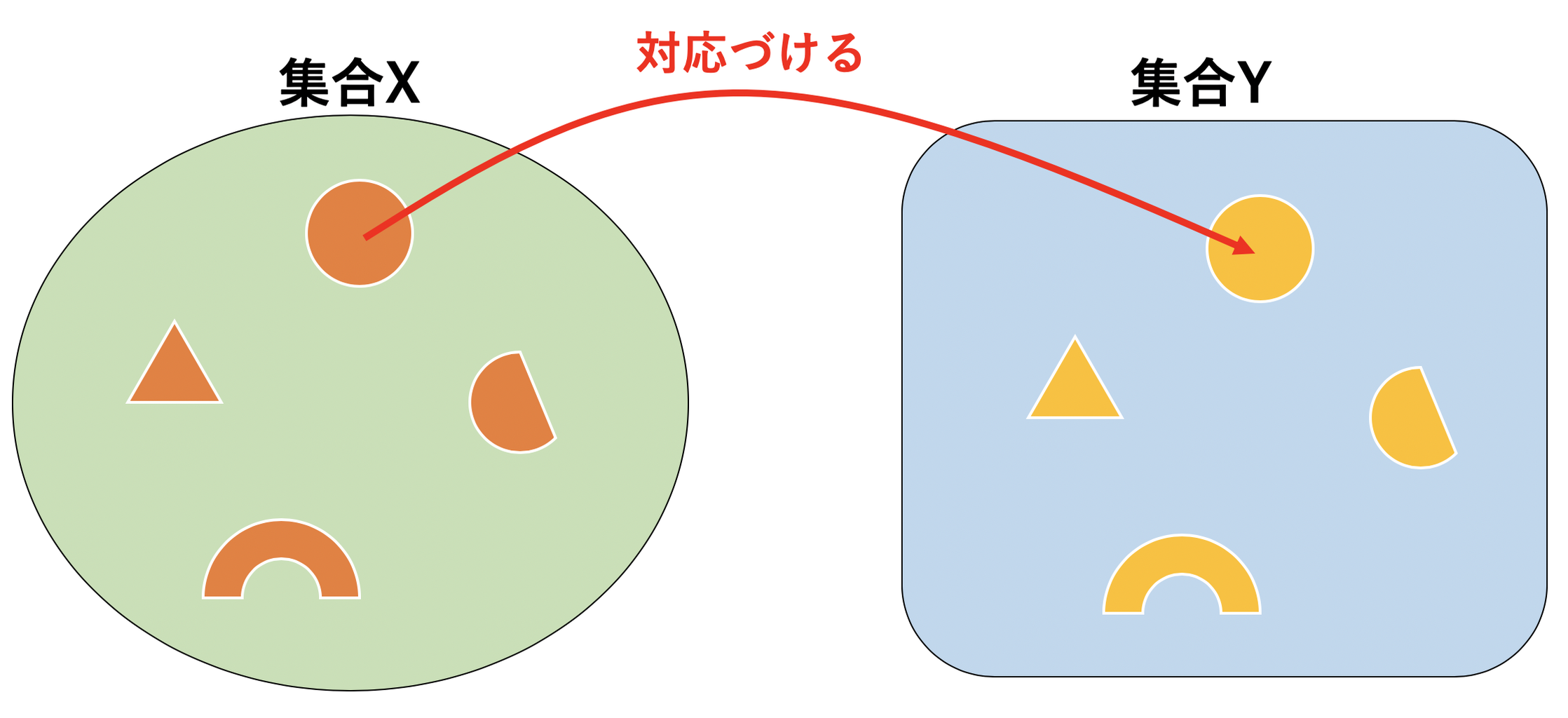
理系ミニマリストのひまつぶしブログ・基礎数学関係 / ・備忘録 写像とは コメント view page

身勝手な主張 view page

【送料無料】3大銘醸地入り!世界の選りすぐり赤・白・スパークリングワイン飲み比べ12本セット 第29弾 【9000178】 | 金賞 飲み比べ ワイン ワインセット ミックス wine wainn…view page

群論の同型定理について view page

「逆写像って？」【論理と集合シリーズ】写像編 その9 view page

halJam's diary 今度こそわかるガロア理論 芳沢光雄 view page

【 送料無料 】48％OFF 三大銘醸地＆金賞入り!世界の辛口白ワイン12本セット 第66弾 白ワイン ワインセット 辛口 【7787426】view page

Yahoo!知恵袋数学Bについて 数列{an}の初項から第n項までの和をΣを用いて表せ という問題がわかりません 例えば 1、3、9、27、…… だとします 答えをみてΣ3のk-１乗となっており 確かにそうだ、と答えを view page

準同型定理 view page