【2枚目20%OFFクーポン配布中!】 カーテン 4枚セット 2枚セット 遮光カーテン カーテン 遮光 1級 レース セット UVカット オシャレ 北欧 断熱 遮熱 無地 タッセル 幅100 丈…

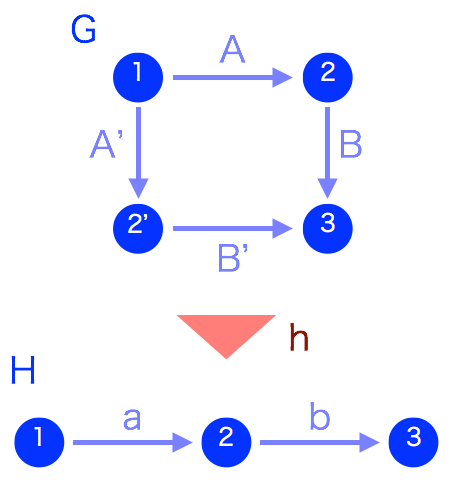
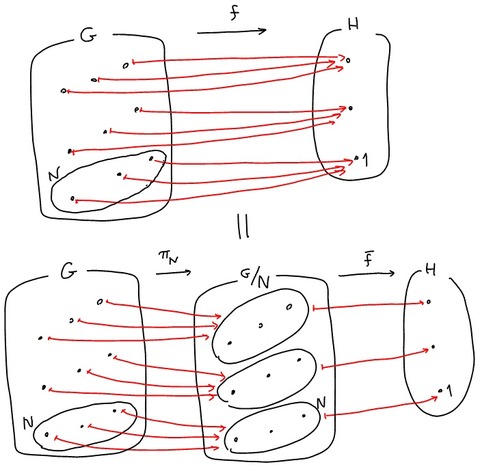
数学カフェAdvent calendar2017 12_18〜圏論に於ける準同型定理〜数学カフェAdvent calendar2017 12_18〜圏論に於ける準同型定理〜
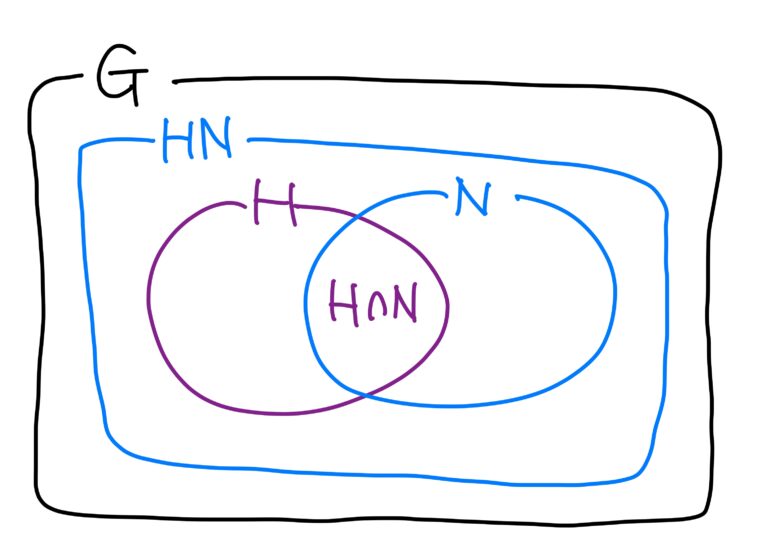
「第二同型定理の証明」重要な定理です!【代数学の基礎シリーズ】群論編 その7
![[本日P5倍] マットレス 高反発 シングル 三つ折りマットレス 敷布団 敷き布団 三つ折り 高反発マットレス セミダブル ダブル 極厚10cm 3つ折り 消臭 メッシュ生地 ベッドマットレス シングルマットレス セミダブルマットレス ダブルマットレス](https://thumbnail.image.rakuten.co.jp/@0_mall/dondon/cabinet/xlm005_9.jpg?_ex=300x300)
[本日P5倍] マットレス 高反発 シングル 三つ折りマットレス 敷布団 敷き布団 三つ折り 高反発マットレス セミダブル ダブル 極厚10cm 3つ折り 消臭 メッシュ生地 ベッドマットレス…

f:id:Natsu1014_brog:20210415113556p:plain

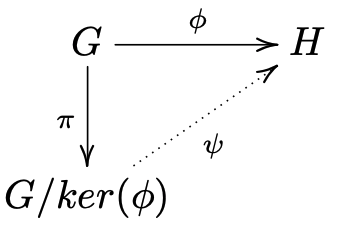
ψの一意性は準同型定理に限らず、一般的に言えますよね? つまり、g⚪︎f=hでfが全射ならはgは一意

ワンランク上の寝心地&耐久性 極厚22cm ニット生地 トリプルエッジサポート ポケットコイル マットレス ポケットコイルマットレス コイルマットレス ベッドマットレス ベッド…

KYUTAMのブログ 準同型定理も一通り終わったという感じ。まぁ後は演習とかで理解を深める方向で行けばいいかな

【★87%OFF⇒2,090円~★】敷きパッド 冬用 あったか ボックスシーツ 冬 ベッドシーツ ベッドカバー ボアシーツ シングル/セミダブル/ダブル 厚手 フランンネル 敷き布団カバー…

累計80万セット突破 固綿入り敷き布団で寝心地UP 布団セット 洗える 増量 抗菌 防臭 防カビ ほこりが出にくい シングル セミダブル ダブル 枕 ふとんセット 組布団 寝具セット 布団…
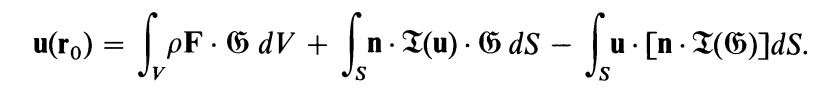
后端 表示定理(Representation Theorem) 后端 表示定理(Representation Theorem) 问题:步骤:

【まとめ購入クーポン配布中!】遮光1級 カーテン 4枚セット 遮光 1級 フック付き 完全遮光 遮光カーテン 4枚セット カーテン 1級 おしゃれ 遮光1級 ミラー 2枚組 UVカット カーテン…

【P5倍★31日23:59まで】ベッド シングルベッド すのこベッド ホープ 3段高さ調節 宮棚あり 2口コンセント付 ベッドフレーム 収納 通気性 低圧メラミン 傷に強い ベッド シングル 宮…
![[数量限定] 半額クーポン1/1-1/3 【ZIP!キテルネで紹介されました!】 毛布 NERUS 【正規品】 ふわとろ毛布 もこもこ毛布 ブランケット モコモコ とろとろ ふわふわ 毛布 シングル セミダブル ダブル ハーフ ふわもこ ポコポコ ひざ掛け 2枚合わせ 厚手 秋冬 Branchpoint](https://thumbnail.image.rakuten.co.jp/@0_mall/t-interior/cabinet/item/usual/htc18_a.jpg?_ex=300x300)
[数量限定] 半額クーポン1/1-1/3 【ZIP!キテルネで紹介されました!】 毛布 NERUS 【正規品】 ふわとろ毛布 もこもこ毛布 ブランケット モコモコ とろとろ ふわふわ 毛布…
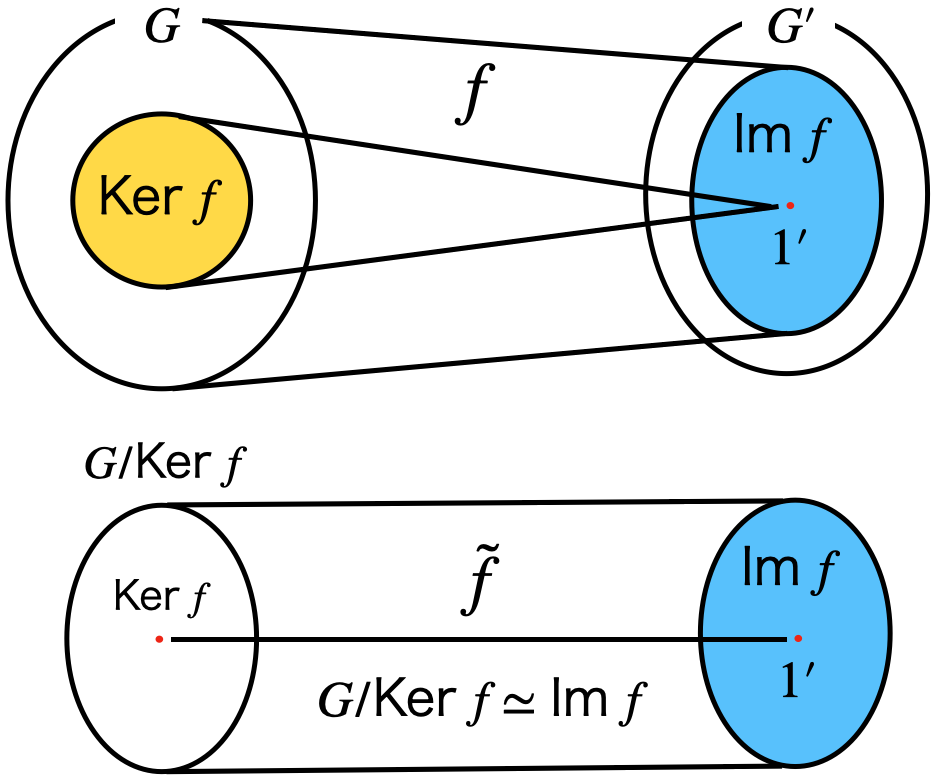
【勉強ノート】群論をわかりやすくまとめてみた【勉強ノート】群論をわかりやすくまとめてみた

数学カフェAdvent calendar2017 12_18〜圏論に於ける準同型定理〜数学カフェAdvent calendar2017 12_18〜圏論に於ける準同型定理〜

【最大72%オフクーポン】★即納★ 5面開閉 折りたたみ 収納ボックス 収納 折りたたみ キャスター付き 衣類ケース コンテナケース ふた付き 可愛い 透明 プラスチック 大きい 重なる 押し入れ…

応用数学、純粋科学、心理学ーあるいは測定の環(WEBアーカイブ版)応用数学、純粋科学、心理学ーあるいは測定の環(WEBアーカイブ版)

1/1-1/3 対象商品10%OFFクーポン 【新商品】 NERUS ふわとろ毛布 Air AirPremium 【正規品】 毛布 ブランケット もこもこ毛布 モコモコ とろとろ ふわふわ…
![\begin{align*} (h \circ g)(x) &= h(g(x)) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}} \circ \widetilde{g^{-1}})(g(x)) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})(\widetilde{g^{-1}}(g(x))) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})([x]_{g}) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})(\pi_{g}(x)) \\ &= ((i_{Z} \circ \tilde{f}) \circ (\widetilde{\mathrm{id}_{X}} \circ \pi_{g}))(x) \\ &= ((i_{Z} \circ \tilde{f}) \circ ( \pi_{f} \circ \mathrm{id}_{X}))(x) \\ &= (i_{Z} \circ \tilde{f})([x]_{f}) \\ &= i_{Z}(f(x)) \\ &= f(x) \end{align*}](https://restmath.com/wp-content/ql-cache/quicklatex.com-6cf55b0d7260a0ca6a3c20ff80b41c51_l3.png)
\begin{align*} (h \circ g)(x) &= h(g(x)) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}} \circ \widetilde{g^{-1}})(g(x)) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})(\widetilde{g^{-1}}(g(x))) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})([x]_{g}) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})(\pi_{g}(x)) \\ &= ((i_{Z} \circ \tilde{f}) \circ (\widetilde{\mathrm{id}_{X}} \circ \pi_{g}))(x) \\ &= ((i_{Z} \circ \tilde{f}) \circ ( \pi_{f} \circ \mathrm{id}_{X}))(x) \\ &= (i_{Z} \circ \tilde{f})([x]_{f}) \\ &= i_{Z}(f(x)) \\ &= f(x) \end{align*}

f:id:frecafloros:20201231201634p:plain

数学カフェAdvent calendar2017 12_18〜圏論に於ける準同型定理〜数学カフェAdvent calendar2017 12_18〜圏論に於ける準同型定理〜

エアーベッド<■爆売れ商品■楽天1位!歳末感謝¥6,990→5,530>電動エアーマット 簡易ベッド 電動ベッド 電動ポンプ内蔵 空気ベッド 自動膨張 枕付き 寝心地 エアーマットレス 折りたたみ…

Yahoo!知恵袋a<0で、2次関数y=x^2+ax-2aの最大値が5になるように、定数aの値を求めよ。
解き方を教えて下さい。
よろしくお願いします。

【まとめ購入クーポン配布中!】カーテン 1級遮光 ミラーレースセット 遮光率99.99% 完全遮光 遮光率100% フック装着済み 4枚セット 2枚セット 幅150cm1枚 遮音 断熱 遮熱 保温…
【勉強ノート】群論をわかりやすくまとめてみた【勉強ノート】群論をわかりやすくまとめてみた

★即納★《3年連続 最も売れた羽毛布団》レビュー1万件超 日本製 W防ダニ 羽毛布団 ホワイトダックダウン 93% 400dp以上 洗える 30マスキルト 掛け布団 掛布団 羽毛ふとん…

Yahoo!知恵袋大学1回生の者ですが、2次元平面の部分集合のあたりが、持っている微分積分の教科書には載っていないため、自習することができません。
![\begin{align*} (h \circ g)(x) &= h(g(x)) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}} \circ \widetilde{g^{-1}})(g(x)) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})(\widetilde{g^{-1}}(g(x))) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})([x]_{g}) \\ &= (i_{Z} \circ \tilde{f} \circ \widetilde{\mathrm{id}_{X}})(\pi_{g}(x)) \\ &= ((i_{Z} \circ \tilde{f}) \circ (\widetilde{\mathrm{id}_{X}} \circ \pi_{g}))(x) \\ &= ((i_{Z} \circ \tilde{f}) \circ ( \pi_{f} \circ \mathrm{id}_{X}))(x) \\ &= (i_{Z} \circ \tilde{f})([x]_{f}) \\ &= i_{Z}(f(x)) \\ &= f(x) \end{align*}](https://restmath.com/wp-content/ql-cache/quicklatex.com-6cf55b0d7260a0ca6a3c20ff80b41c51_l3.png)





![[本日P5倍] マットレス 高反発 シングル 三つ折りマットレス 敷布団 敷き布団 三つ折り 高反発マットレス セミダブル ダブル 極厚10cm 3つ折り 消臭 メッシュ生地 ベッドマットレス シングルマットレス セミダブルマットレス ダブルマットレス](https://thumbnail.image.rakuten.co.jp/@0_mall/dondon/cabinet/xlm005_9.jpg?_ex=300x300)









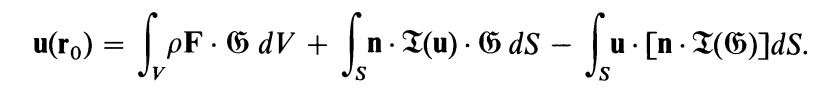




![[数量限定] 半額クーポン1/1-1/3 【ZIP!キテルネで紹介されました!】 毛布 NERUS 【正規品】 ふわとろ毛布 もこもこ毛布 ブランケット モコモコ とろとろ ふわふわ 毛布 シングル セミダブル ダブル ハーフ ふわもこ ポコポコ ひざ掛け 2枚合わせ 厚手 秋冬 Branchpoint](https://thumbnail.image.rakuten.co.jp/@0_mall/t-interior/cabinet/item/usual/htc18_a.jpg?_ex=300x300)