Images of 局所環

局所環と非単元の集合　Local ring局所環と非単元の集合　Local ring view page

【最大17%OFF+ライブ視聴で1500円OFFクーポン】 枕 枕カバー 付 ヒツジのいらない枕 父の日 プレゼント 実用的 健康グッズ 誕生日 ギフト 洗える 通気性 横向き寝用枕 うつぶせ寝…view page

ムラサキマサリを用いた高度循環型醸造に関する産官学研究 椛田 聖孝 view page

実践編-1：抗シガトキシン抗体の相互作用解析例（4） view page

cov17724のブログ Prime avoidanceについて view page

楽天1位【924円～79％OFFクーポンで】収納ボックス 折り畳み ふた付き プラスチック キャスター付き 大容量 折り畳み可能 5面開き 組み立て簡単 押入れ収納 衣装収納 お洒落 寝室 新生活…view page

Take-Home Midterm view page

2014/1/31 ”解析学 II view page

「局地的」と「局所的」の違い view page

レビュー特典あり とろとろケット NERUS 正規品 洗える 掛け布団 布団 タオルケット ブランケット 肌掛け布団 肌布団 くしゅくしゅケット とろーり とろける とろとろ ケット 夏用…view page

職場環境測定 view page

マクロリーン級数マクロリーン級数 view page

日環研の 局所換気装置 - JER view page

【タイムセール実質:3,121円！60%OFFクーポンで】スラックスハンガー 大容量 20本掛け スイング式 キャスター付き 押入れ収納 コンパクト クローゼット収納 ズボンハンガー…view page

インフレーション理論 view page

高度な環境性能を誇るデータセンター view page

循環調節機構の作用発現時間 view page

中が透けない 壁付き チェスト スリム/ワイド 幅34/54 奥行41.5/41.7 高さ66.1/86.1/106.1cm タンス 衣装ケース 収納ケース プラスチック 引き出し 洗面所 収納…view page

浮腫の種類と特徴 view page

P Cyg プロファイル view page

24時間換気（計画換気）のポイント view page

【6/5限定全品対象最大20%OFFクーポン！先着順】壁掛け時計 電波 おしゃれ 時計 壁掛け 掛け時計 電波時計 オシャレ リビング かわいい 北欧 クロック 静音 レトロ 軽量 オフィス…view page

国立がん研究センター東病院分野別治療方針前立腺がん view page

「任意の有限生成加群が射影被覆を持つ」ような環は半局所環である view page

べき関数型スペクトル view page

【SS期間に使えるクーポン配布中&エントリーでP10倍】【2枚組 1枚あたり5,830円】洗える 肌掛け布団 とろ〜りケット シングル 正規 とろーり マシュマロケット とろとろケット…view page

活動銀河核統一モデル view page

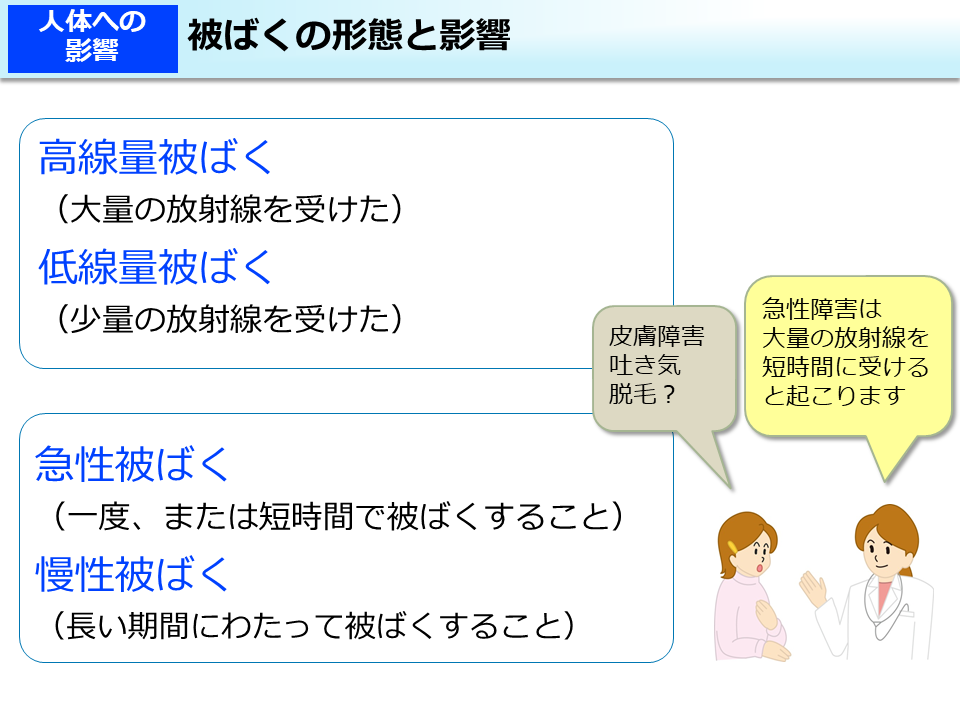
放射線による健康影響等に関する統一的な基礎資料(令和元年度版、 ＨＴＭＬ形式) view page

循環集塵対策例 view page

【78%OFF クーポン利用で968円】 【総合ランキング1位 即納！】収納ボックス 折畳み キャスター付き 5面開閉 収納ケース 押入れ収納 組立簡単 27L/40L/53L/82L 積み重ね…view page

Yahoo!知恵袋1[cm-3]を[ｍ-3]に換算するとどうなりますか？？ 早急にお願いします。 view page

マクロリーン級数 view page

81 view page

＼スーパーセール半額／【楽天1位 理学療法士推奨】枕 低反発枕 肩 首 ストレートネック 横向き RoyalLife 【二度寝注意枕】 女性 横向き寝 快眠枕 睡眠枕 まくら 頭 解消 頚椎安定型…view page

第2kame日記 局所環 view page

集塵機 周辺情報　1-4.粉塵に関する法令 view page

商環 view page

【日本No.1受賞】ハグモッチ 正規品【さらに改善】【医師の92%が推奨】20万人の眠りを変えた 枕 ふわもち 腰 肩 首 いびき防止 抱き枕 妊婦 誕生日プレゼント 人をダメにする クッション…view page

商環 view page

R は可換環で乗法の単位元をもつものとする.R の任意のイデ アルの減少列 I1 ⊃I2 ⊃I3 ⊃··· に対して In =In+1 =··· となる n が存在するとき,R をArtin 環という.R が Artin 環であるとき,以下の命題が成り立つことを証明せよ.(1) f : R → S が全射環準同型ならば,S も Artin 環である. (2) R が整域ならば,R は体である.証明[堀田良之]環と体1p61SのイデアルIに対し、𝑓−1 𝐼 もイデアルであることに従う。(2) R が整域ならば,R は体である.証明RがArtin整域で0 ≠ a ∈ Rなら,(an) = (an+1)となる整数n > 0が存在し,ある (x ∈ A) に対し an = xan+1 となり,an(1 − ax) = 0,即ち 1 = ax が得られ,R は体であるこ とが従う。(3) R の素イデアルは極大イデアルである.[堀田良之]環と体1p５８f:R→R/I、f(a)=a+Iと定めると、fは全射環準同型写像である。よって(1)よりR/Iはアルティン環である。また、IをRの素イデアルとすると、剰余環R/Iは整域である。いま(2)より、R/Iは体である。このことは、Iが極大イデアルであることと同値である。ゆえに、IはRの極大イデアルである。(4) R の異なる素イデアルの個数は有限である[堀田良之]環と体1p５８ view page

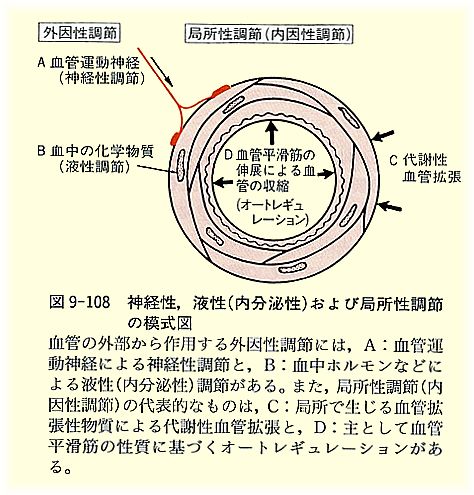
微小循環②（血管の神経性調節）_c0229463_15585396.jpg view page

＼1,240円～クーポン利用で♪ 【楽天1位 理学療法士 整体師 推奨】 枕 横向き寝 低め 低反発枕 肩 首枕 いびき 防止 快眠枕 ストレートネック枕 いびき防止枕 人をダメにする枕 まくら…view page

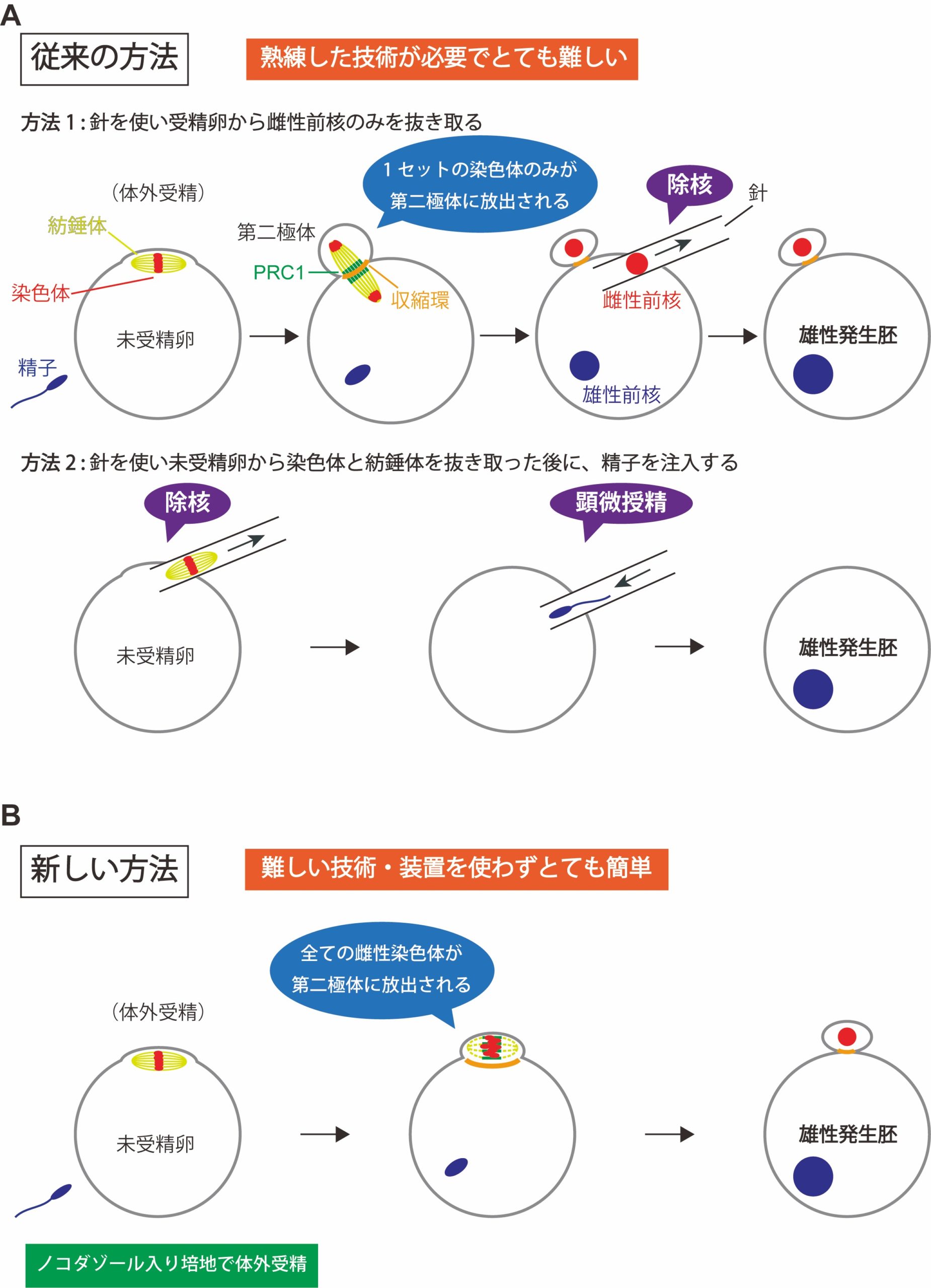
難しい技術を使わずに受精卵から卵子の染色体だけを取り除くことに成功〜簡便な雄性発生胚作出法〜 view page

圖：北環綫擬議鐵路方案 view page

yoshitake-hのブログ 松村「可換環論」§13. 次数環，Hilbert 関数，Samuel 関数 view page

【SS期間に使えるクーポン配布中&エントリーでP10倍】楽天総合1位 とろ〜りケット 洗える 肌掛け布団 正規 春 夏 マシュマロケット ダウンケット 羽毛肌掛け布団 を検討の方に…view page

環の局所化~定義とその気持ち~ view page

「局所的」「局地的」の意味と違いその他おすすめのコンテンツ一覧 view page

環 view page

【5のつく日×40％OFFクーポン】折りたたみ椅子 折り畳みチェア 収納袋付き 軽量 工具不要 コンパクト アウトドア キャンプ 野外 折りたたみチェア アウトドアチェア キャンプ椅子 簡単収納…view page

画像 view page