Images of 帰納的可算集合

Mission Driven Brand 演繹法とは｜演繹的思考の例と推論の手順を図解解説 view page

【 IZUMIYA 】100口限定！確率1/10で 響ブレンダーズチョイス が当たる！ ウイスキーくじ ＼運試しに挑戦！／ 響BLENDER'S CHOICE 響BC 響 くじ ウイスキーくじ…view page

sumiiのブログ 帰納的定義ということ view page

とある数学科大学生の備忘録 可算集合 view page

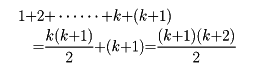
数学的帰納法（読み）すうがくてききのうほう（英語表記）mathematical induction view page

【最強配送】【送料無料】アサヒスーパードライ キンキン冷感タンブラー2個付き 350ml×2ケース/48本【北海道・沖縄県・東北・四国・九州地方は必ず送料がかかります】view page

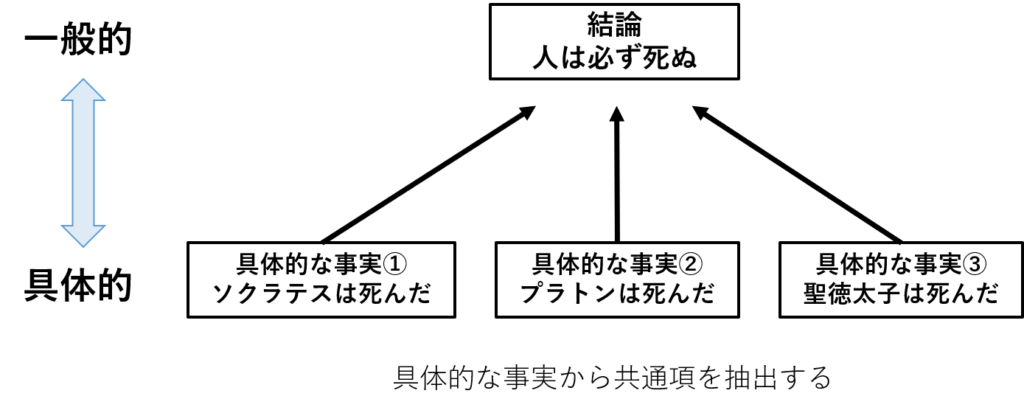
【論理的思考】演繹法と帰納法を使った論理展開【簡単解説】 スポンサーリンクカテゴリーカテゴリー view page

チューリングの停止性問題 Iij Engineers Blog view page

順序数入門　Ver.ω順序数入門　Ver.ω view page

先行予約品　厚岸蒸溜所　シングルモルトジャパニーズウイスキー厚岸立夏　イチローズモルトホワイトラベル　飲み比べセット 　ジャパニーズウィスキー 　5月下旬順次発送view page

数学的帰納法は帰納ではない？数学的帰納法は帰納ではない？ view page

「演繹的・帰納的」な推論の定義、違いを、具体例を交えて解説 view page

数学的帰納法の考え方・理論・注意点、様々な帰納法 view page

【最強配送】【送料無料】アサヒスーパードライ キンキン冷感タンブラー1個付き 350ml×1ケース/24本【北海道・沖縄県・東北・四国・九州地方は必ず送料がかかります】view page

演繹的思考帰納的思考 view page

帰納的議論・前提の関連性４ view page

数学的帰納法は帰納ではない？ 数学的帰納法は帰納ではない？ view page

【 特別 送料無料 】 1本たったの598円(税込) 3大銘醸地入り 世界選りすぐり赤ワイン11本セット 第260弾【7784520】 | 金賞 飲み比べ ワイン ワインセット wine…view page

ロジカルシンキング～帰納法・演繹法(前半)～ view page

数学的帰納法①（等式） view page

分析・総合、演繹・帰納 view page

アサヒ スーパードライ 缶(350ml*48本セット)【アサヒ スーパードライ】view page

帰納法 view page

演繹法と帰納法をバランスよく使う.jpg view page

3TRIAL数学B-225解答 view page

日時指定必須 送料無料 ブラックニッカ 4L×4本 クリア 37度 4000ml アサヒ ニッカ ウィスキー ペット 大容量 業務用 包装不可 15時決済で365日即日発送・日時指定必須 同梱不可…view page

ネットジャーナル３１ view page

帰納法の論理を図式化して確認 view page

大人の少年で、僕はありたい。 人生はつまり数学的帰納法 view page

【05/23 20:00～ エントリーで最大ポイント5倍】【スタンプラリー最大ポイント5倍】アサヒ スーパードライ 350ml 缶 24本 1ケース【送料無料（一部地域除く）】 アサヒビールview page

「同じ」点を探せば、帰納法や演繹法が理解できる view page

数学的帰納法 view page

怜悧玲瓏　～高校数学を天空から俯瞰する～ 十六夜♪ view page

こだわり酒場のレモンサワー350ml缶( 350ml×48本セット)【rb_dah_kw_2】【こだわり酒場のレモンサワー】[レモンサワー 缶チューハイ]view page

マスログ論理的思考術　帰納法と演繹法って何？難病の検査で陽性反応！・・・実際に罹患している確率は何パーセント...KPIとは何かやさしく学ぶ統計学～ピボットテーブルを使ったデータの集計と可視化...分数の足し算とは【算数からやさしく解説】小数の割り算のやり方【算数からやさしく解説】大人が学ぶ算数 ―和・差・積・商って？計算の順序ときまり...難病の検査で陽性反応！・・・実際に罹患している確率は何パーセント...KPIとは何か社内の自己啓発学習を活性化させる方法 view page

kazz の数学旅行記 数学的帰納法による証明の記述の仕方について view page

数学的帰納法　基本と応用 view page

【企画品】サントリープレミアムシングルモルトウイスキーセット(白州12年／ボウモア12年)(1セット)view page

kakkol habe（移行版） 　帰納的聖書研究法 view page

数学的帰納法とは？入試問題付きで全5パターンをわかりやすく解説！ view page

数学的帰納法の意味 view page

【05/24入荷予定】【05/23 20:00～ エントリーで最大ポイント5倍】数量限定 アサヒ スーパードライ キンキン冷感タンブラー付 350ml 缶…view page

Yahoo!知恵袋「帰納的に」 view page

cci20161124-%e3%81%ae%e3%82%b3%e3%83%94%e3%83%bc-2 view page

photo view page

ブラントン 正規品 [箱付] 750ml Blanton's バーボン 宝酒造 ※6本まで1個口で発送可能父の日 暑中見舞い ギフト 御祝 熨斗view page

画像 view page

PDFはこちら view page

『英語職人』時吉秀弥の英文法　最終回答！可算不可算と単複同形の区別２：fishについて view page

【企画品】サントリー 生ビール キャノーラ油付(350ml×24本)【サントリー生】view page

【イメージ理解】可算名詞と不可算名詞の見分け方【単語まとめ】 view page

たかだか可算集合の部分集合はたかだか可算集合である。これを証明するのに選択公理は必要ですか？ 写真の view page