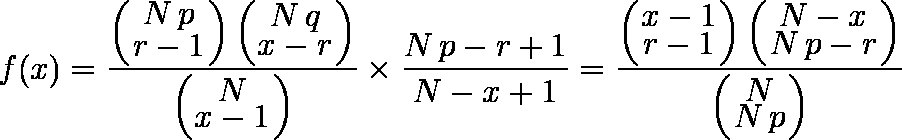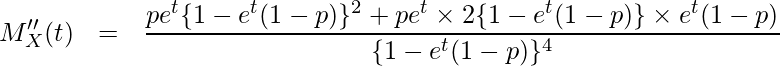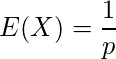お歳暮 2025 ビール 数量限定 当店限定 お歳暮 ビール ギフト セット 最大250円オフクーポン対象 指定地域送料無料 サントリー 4種 12缶 BPH3SS 御歳暮 歳暮 プレゼント…

Juliaで学ぶ確率変数(3) - 幾何分布(離散型)1.幾何分布 Ge(p)

お歳暮 2025 ビール お歳暮 ビール ギフト セット 最大250円オフクーポン対象 指定地域送料無料 サントリー 5種 18缶 BM5AE 御歳暮 歳暮 プレゼント 詰合せ こだわり…

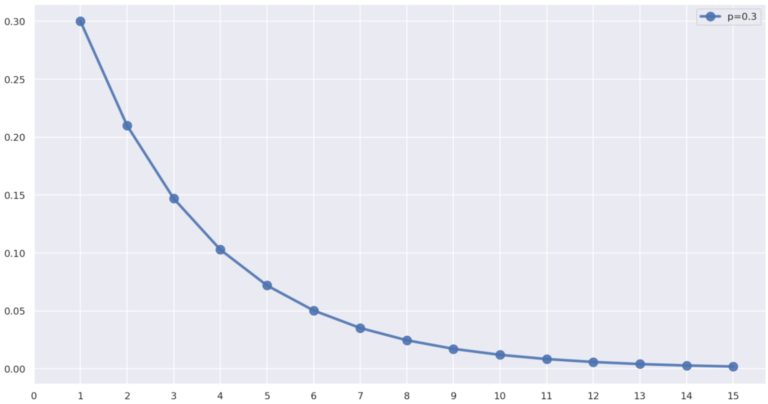
反比例っぽいグラフはどのようにして生まれるのか?前略反比例のグラフ草々

お歳暮 ビール ギフト セット 2025【本州のみ 送料無料】アサヒ AS-3N 『GIFT』スーパードライ 詰め合わせ 内祝い 誕生日 プレゼント お酒 贈り物 3000円以下 お年賀 お歳暮…
![アサヒ スーパードライ 缶(500ml*24本入)【2shdrk】【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]](https://thumbnail.image.rakuten.co.jp/@0_mall/soukaidrink/cabinet/806/4901004006806.jpg?_ex=300x300)
アサヒ スーパードライ 缶(500ml*24本入)【2shdrk】【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]
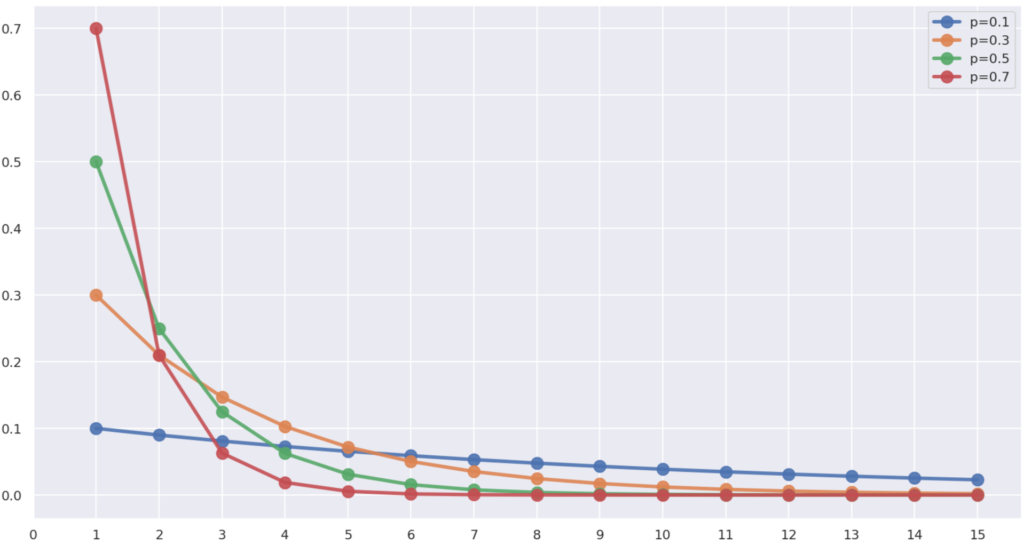
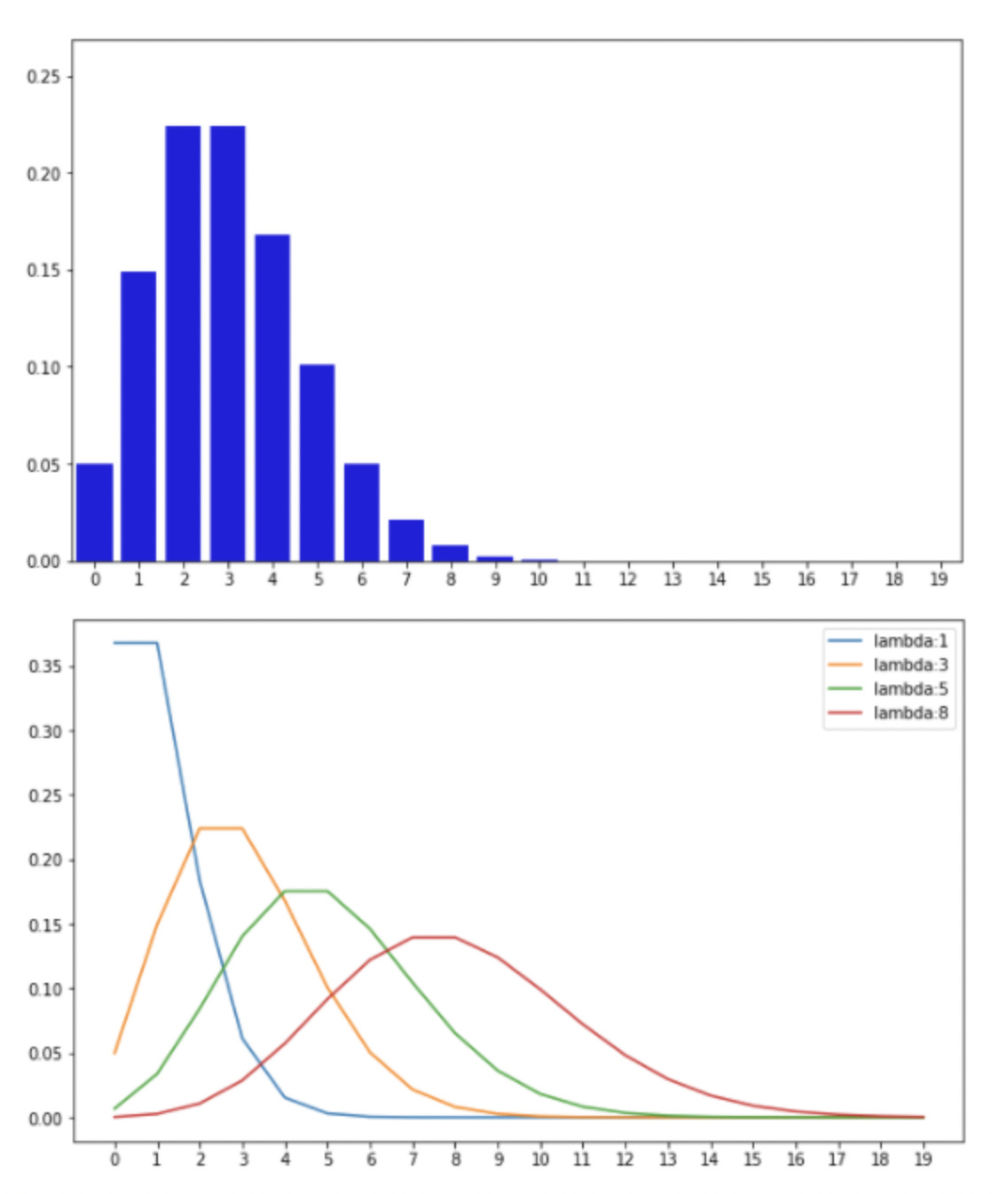
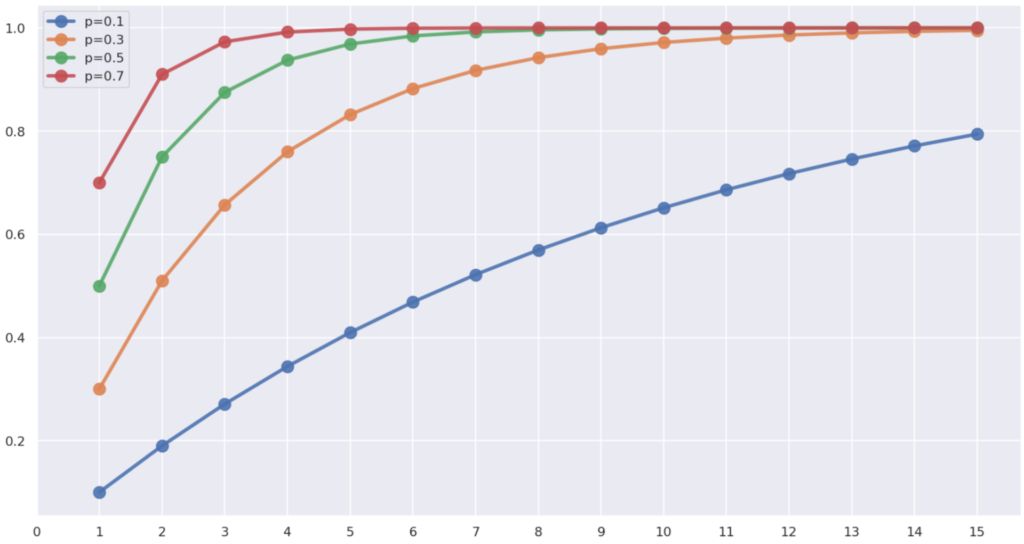
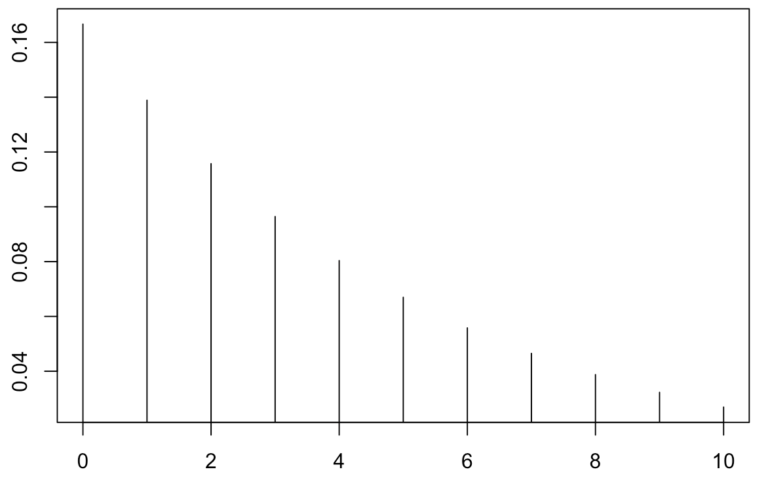
p=0.1,0.3,0.5,0.7と変えたときの,幾何分布の確率(質量)関数の違い
集客に繋がる福岡市のホームページ制作会社アライブキャスト
スタッフブログ
STAFF BLOG
様々な確率分布

【 特別 送料無料 】 1本たったの598円(税込) 3大銘醸地入り 世界選りすぐり赤ワイン11本セット 第276弾【7784806】 | 金賞 飲み比べ ワイン ワインセット wine…

f:id:yanbow221:20170902095612p:plain

【今だけP7倍★12/16迄】 【150円引クーポン配布中】 【全国送料無料】 お歳暮 冬ギフト ギフト ビール エビス 恵比寿 12本 ギフト プレゼント サッポロビール 飲み比べ…
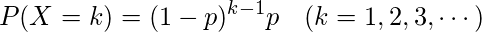
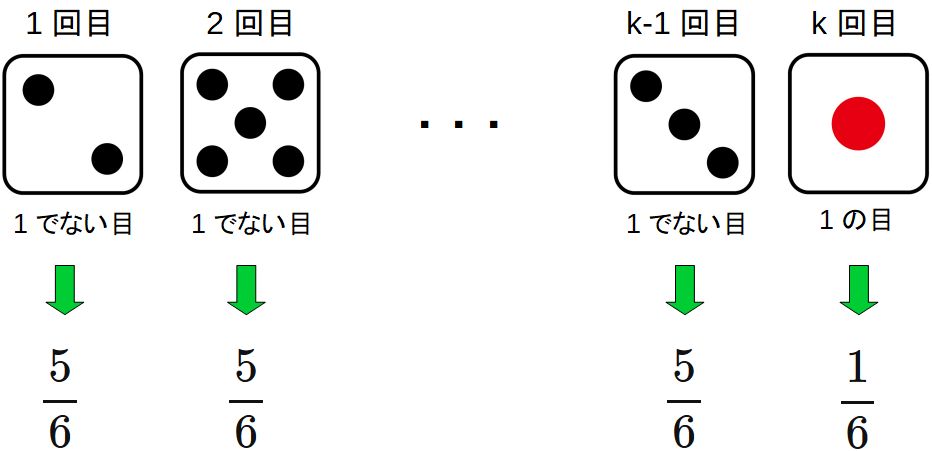
\begin{eqnarray*} P(X=k)=(1-p)^{k-1} p & (k=1,2,3,\cdots) \\ \end{eqnarray*}

サントリー ビール ザ・プレミアム・モルツ(350ml*24本入)【ザ・プレミアム・モルツ(プレモル)】

f:id:ganbaru_engineer:20190806002214p:plain
![アサヒ スーパードライ 缶(350ml*48本セット)【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]](https://thumbnail.image.rakuten.co.jp/@0_mall/soukaidrink/cabinet/557/62557.jpg?_ex=300x300)
アサヒ スーパードライ 缶(350ml*48本セット)【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]
![\begin{eqnarray*} \displaystyle E[X^2]-(1-p)E[X^2] &=& pE[X^2] \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - (1-p)\sum_{x=0}^n (2x+1)(1-p)^{x} \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - \sum_{x=0}^n (2x+1)(1-p)^{x+1} \\ &=& \left\{ 1 \times (1-p)^{0} + 3 \times (1-p)^{1} + 5 \times (1-p)^{2} + \dots \right\} \\ && - \left\{ 1 \times (1-p)^{1} + 3 \times (1-p)^{2} + 5 \times (1-p)^{3} + \dots \right\} \\ &=& \left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 2 \times (1-p)^{2} + \dots \right\} \\ &=& 1 + 2 \times \sum_{x=1}^n (1-p)^{x} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-body/wp-content/ql-cache/quicklatex.com-c324430bc575ce6f0fb2f9136bd6400e_l3.png)
\begin{eqnarray*} \displaystyle E[X^2]-(1-p)E[X^2] &=& pE[X^2] \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - (1-p)\sum_{x=0}^n (2x+1)(1-p)^{x} \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - \sum_{x=0}^n (2x+1)(1-p)^{x+1} \\ &=& \left\{ 1 \times (1-p)^{0} + 3 \times (1-p)^{1} + 5 \times (1-p)^{2} + \dots \right\} \\ && - \left\{ 1 \times (1-p)^{1} + 3 \times (1-p)^{2} + 5 \times (1-p)^{3} + \dots \right\} \\ &=& \left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 2 \times (1-p)^{2} + \dots \right\} \\ &=& 1 + 2 \times \sum_{x=1}^n (1-p)^{x} \\ \end{eqnarray*}

赤ワイン フルボディ セット ワインセット 赤 ワイン ギフト 箱 京橋ワイン 京橋わいん 6本 750ml 飲み比べ プレゼント 送料無料 パーカー 【 第150弾 すべてパーカー…
練習問題 : モンテカルロ統計計算 Chapter 5 ギブスサンプリング

お歳暮 ビール ギフト セット 2025【本州のみ 送料無料】アサヒ AS-5N『GIFT』スーパードライ 詰め合わせ 内祝い 誕生日 プレゼント お酒 贈り物 お年賀 お歳暮 冬ギフト

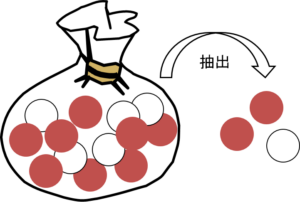
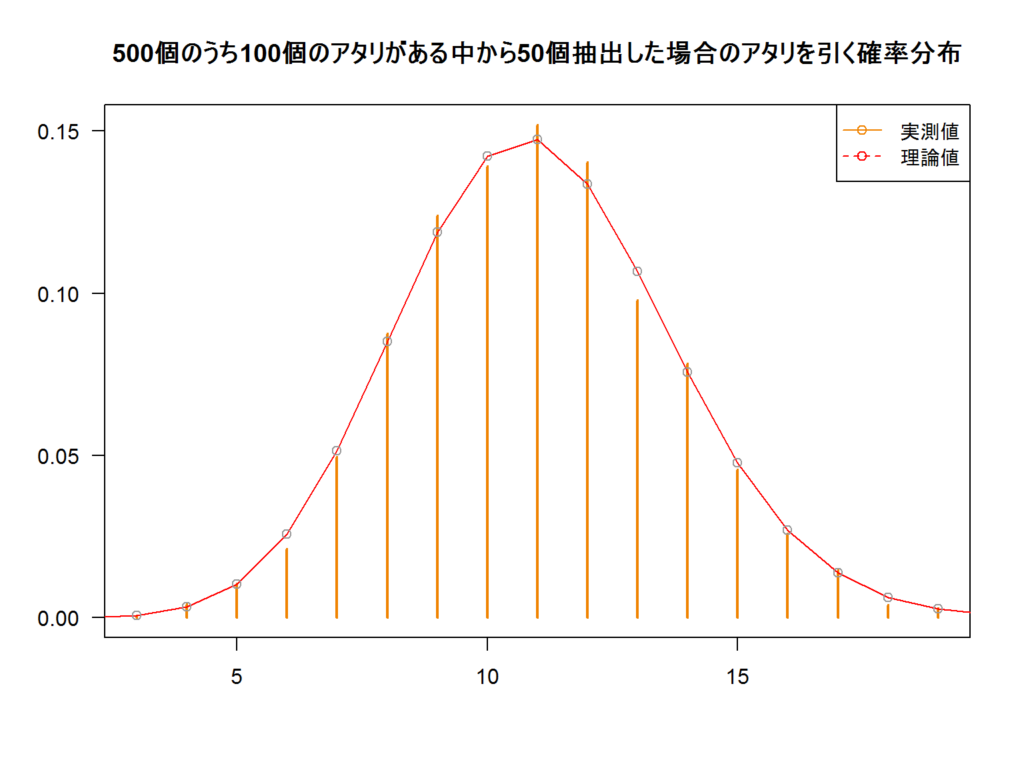
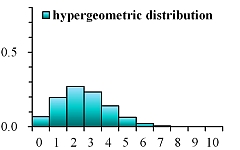
超幾何分布超幾何分布 (hypergeometric distribution)ざっくりした説明二項分布との関係確率分布であることの確認期待値の導出分散の導出参考
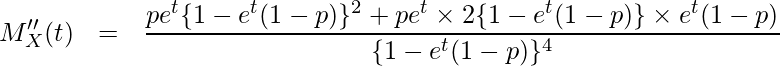
\begin{eqnarray*} \displaystyle M''_X(t) &=& \frac{pe^t\{1-e^t(1-p)\}^2+pe^t \times 2\{1-e^t(1-p)\} \times e^t(1-p)}{\{1-e^t(1-p)\}^4} \end{eqnarray*}

【本州のみ 送料無料】お歳暮 ビール ギフト 飲み比べ セット 2025 サッポロ エビス YNF3D『GIFT』恵比寿 ヱビス 高級 詰め合わせ 内祝い 誕生日 プレゼント お酒 贈り物 ビール…

f:id:nishiru3:20180612225718p:plain

【抽選で1等77,777ポイント当たる!】お歳暮 御歳暮 冬ギフト ビール お酒 プレゼント 2025 飲み比べ 詰め合わせ【送料無料】サッポロ エビス 4種の味わいセット YNF3D 1セット…

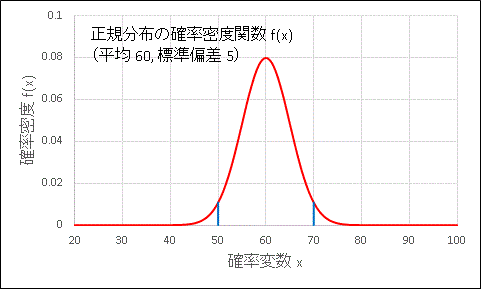
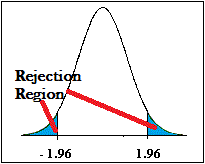
MENUBASIC STUDYPROGRAMMINGAI REPORTABOUT USAVILEN片側検定と両側検定の違いをわかりやすく解説

12/13 10:00〜12/15限定P3倍 【最強配送】【抽選で1等77,777ポイント当たる!】【送料無料】 アサヒ スーパードライ 350ml×2ケース/48本 YTR ビール 辛口…

The Life幾何分布・負の2項分布と中心極限定理の例投稿ナビゲーションタグカテゴリー人気記事言語:最近の投稿
![\begin{eqnarray*} \displaystyle E[X^2]-(1-p)E[X^2] &=& pE[X^2] \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - (1-p)\sum_{x=0}^n (2x+1)(1-p)^{x} \\ &=& \sum_{x=0}^n (2x+1)(1-p)^{x} - \sum_{x=0}^n (2x+1)(1-p)^{x+1} \\ &=& \left\{ 1 \times (1-p)^{0} + 3 \times (1-p)^{1} + 5 \times (1-p)^{2} + \dots \right\} \\ && - \left\{ 1 \times (1-p)^{1} + 3 \times (1-p)^{2} + 5 \times (1-p)^{3} + \dots \right\} \\ &=& \left\{ 1 \times (1-p)^{0} + 2 \times (1-p)^{1} + 2 \times (1-p)^{2} + \dots \right\} \\ &=& 1 + 2 \times \sum_{x=1}^n (1-p)^{x} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-body/wp-content/ql-cache/quicklatex.com-c324430bc575ce6f0fb2f9136bd6400e_l3.png)

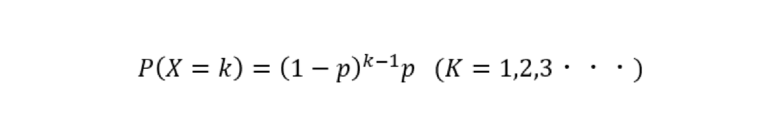







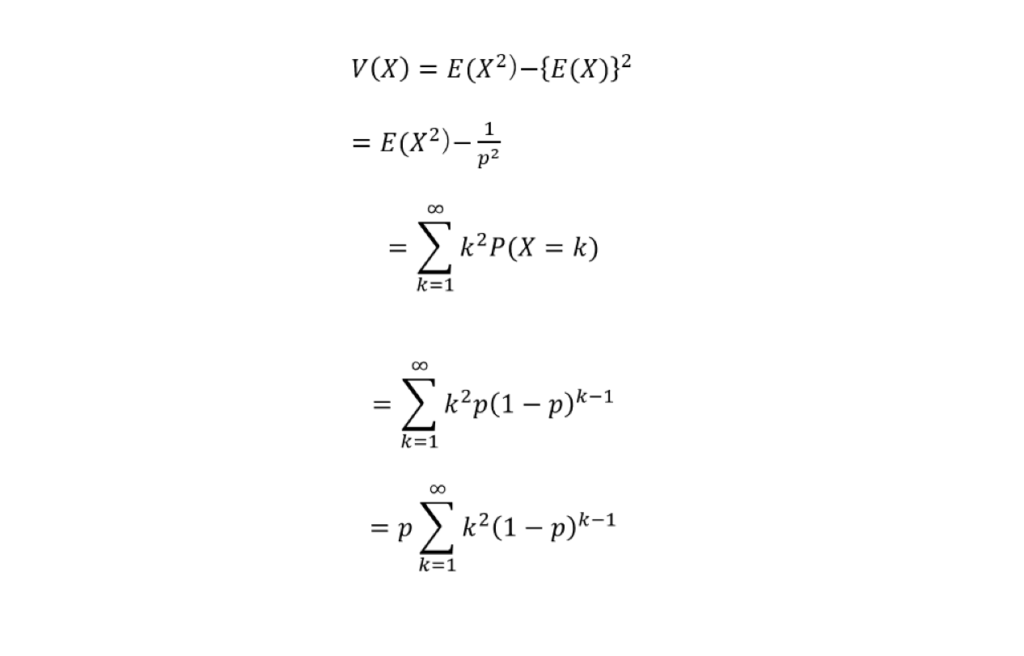
![アサヒ スーパードライ 缶(500ml*24本入)【2shdrk】【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]](https://thumbnail.image.rakuten.co.jp/@0_mall/soukaidrink/cabinet/806/4901004006806.jpg?_ex=300x300)
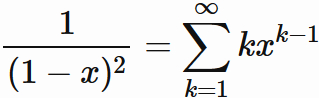






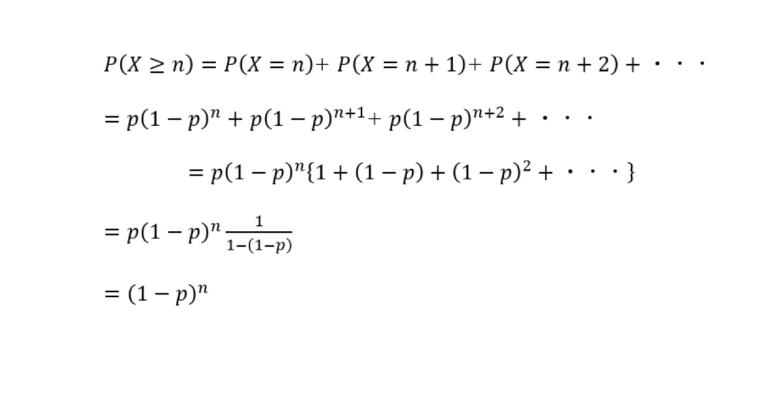

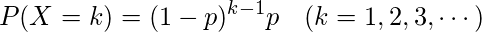



![アサヒ スーパードライ 缶(350ml*48本セット)【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]](https://thumbnail.image.rakuten.co.jp/@0_mall/soukaidrink/cabinet/557/62557.jpg?_ex=300x300)