Images of 正則局所環

日本学士院会員の選定について view page

可換環論の様相 クルルの定理と正則局所環【電子書籍】[ 新妻 弘 ]view page

Uro Tekiteki 局所体に関しては森田康夫 整数論 第6章の演習問題に書いてある模様 本見ないと確信が持てなくなっている自分が悲しい Rt Jvn U 代数体の不分岐拡大はアーベル ここで見た命題でした Http T Co 3rtyaa0 局所環なら正しいのかな view page

ドクター紹介 view page

JavaScript is not available. view page

可換環論の様相 クルルの定理と正則局所環／新妻弘【3000円以上送料無料】view page

第102回薬剤師国家試験　問99 view page

現在登録中の臨床試験 view page

局所環と非単元の集合　Local ring局所環と非単元の集合　Local ring view page

可換環論の様相 クルルの定理と正則局所環／新妻弘【1000円以上送料無料】view page

yoshitake-hのブログ 松村「可換環論」§13. 次数環，Hilbert 関数，Samuel 関数 view page

ムラサキマサリを用いた高度循環型醸造に関する産官学研究 椛田 聖孝 view page

実践編-1：抗シガトキシン抗体の相互作用解析例（4） view page

可換環論の様相　クルルの定理と正則局所環　新妻弘/著view page

cov17724のブログ Prime avoidanceについて view page

Take-Home Midterm view page

2014/1/31 ”解析学 II view page

可換環論の様相 クルルの定理と正則局所環view page

「局地的」と「局所的」の違い view page

職場環境測定 view page

マクロリーン級数マクロリーン級数 view page

【3980円以上送料無料】可換環論の様相　クルルの定理と正則局所環／新妻弘／著view page

日環研の 局所換気装置 - JER view page

インフレーション理論 view page

高度な環境性能を誇るデータセンター view page

可換環論の様相　クルルの定理と正則局所環view page

循環調節機構の作用発現時間 view page

浮腫の種類と特徴 view page

P Cyg プロファイル view page

可換環論の様相 クルルの定理と正則局所環view page

24時間換気（計画換気）のポイント view page

国立がん研究センター東病院分野別治療方針前立腺がん view page

「任意の有限生成加群が射影被覆を持つ」ような環は半局所環である view page

可換環論の様相 クルルの定理と正則局所環 大学数学スポットライト・シリーズ / 新妻弘 【全集・双書】view page

べき関数型スペクトル view page

活動銀河核統一モデル view page

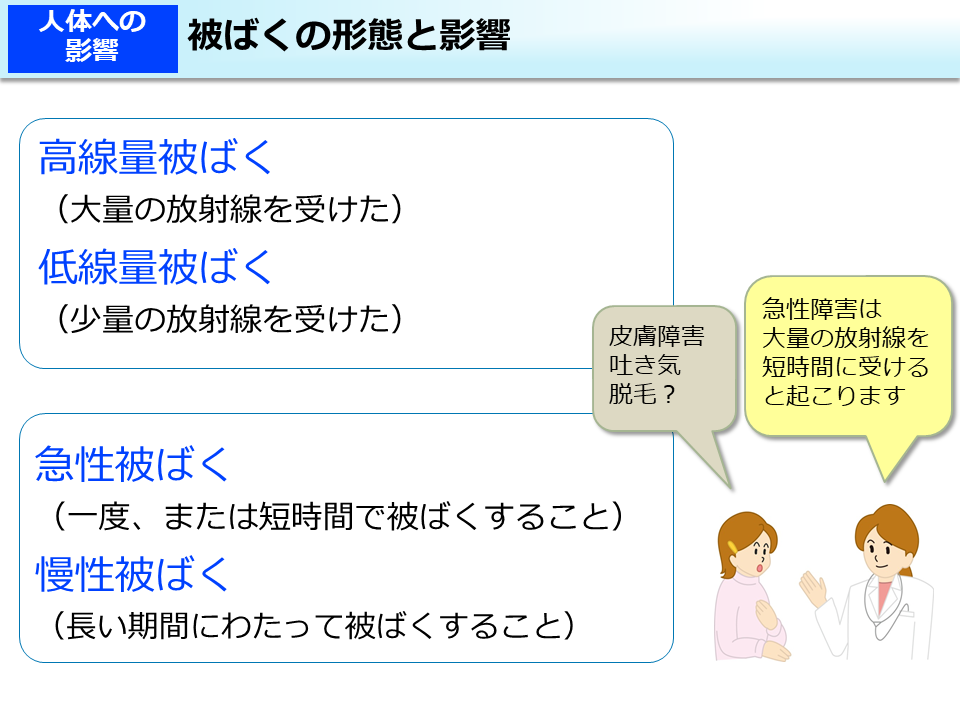
放射線による健康影響等に関する統一的な基礎資料(令和元年度版、 ＨＴＭＬ形式) view page

可換環論の様相 クルルの定理と正則局所環[本/雑誌] (大学数学スポットライト・シリーズ) / 新妻弘/著view page

循環集塵対策例 view page

Yahoo!知恵袋1[cm-3]を[ｍ-3]に換算するとどうなりますか？？ 早急にお願いします。 view page

マクロリーン級数 view page

81 view page

第2kame日記 局所環 view page

集塵機 周辺情報　1-4.粉塵に関する法令 view page

商環 view page

商環 view page

R は可換環で乗法の単位元をもつものとする.R の任意のイデ アルの減少列 I1 ⊃I2 ⊃I3 ⊃··· に対して In =In+1 =··· となる n が存在するとき,R をArtin 環という.R が Artin 環であるとき,以下の命題が成り立つことを証明せよ.(1) f : R → S が全射環準同型ならば,S も Artin 環である. (2) R が整域ならば,R は体である.証明[堀田良之]環と体1p61SのイデアルIに対し、𝑓−1 𝐼 もイデアルであることに従う。(2) R が整域ならば,R は体である.証明RがArtin整域で0 ≠ a ∈ Rなら,(an) = (an+1)となる整数n > 0が存在し,ある (x ∈ A) に対し an = xan+1 となり,an(1 − ax) = 0,即ち 1 = ax が得られ,R は体であるこ とが従う。(3) R の素イデアルは極大イデアルである.[堀田良之]環と体1p５８f:R→R/I、f(a)=a+Iと定めると、fは全射環準同型写像である。よって(1)よりR/Iはアルティン環である。また、IをRの素イデアルとすると、剰余環R/Iは整域である。いま(2)より、R/Iは体である。このことは、Iが極大イデアルであることと同値である。ゆえに、IはRの極大イデアルである。(4) R の異なる素イデアルの個数は有限である[堀田良之]環と体1p５８ view page

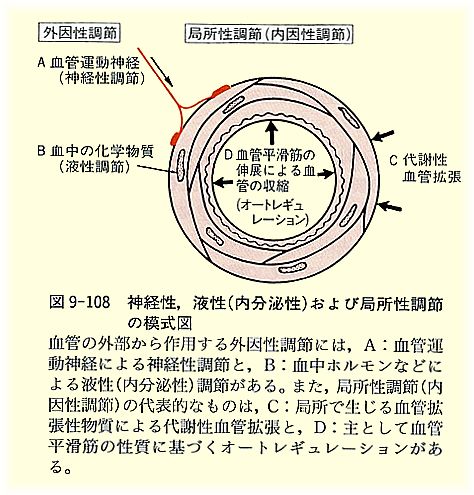
微小循環②（血管の神経性調節）_c0229463_15585396.jpg view page

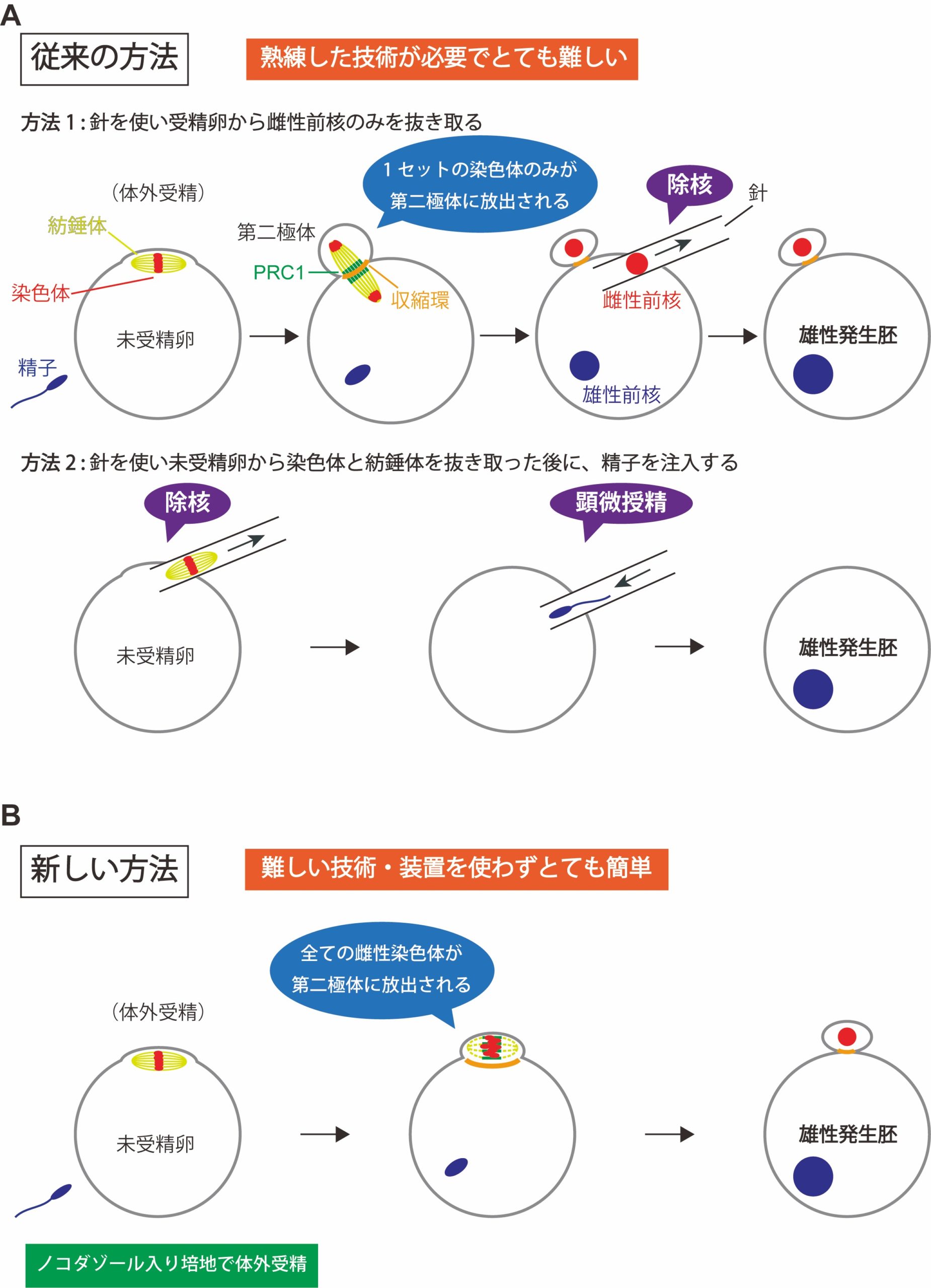
難しい技術を使わずに受精卵から卵子の染色体だけを取り除くことに成功〜簡便な雄性発生胚作出法〜 view page