Images of 不動点定理

中点連結定理解説画像 view page

[新品未開封｜SIMフリー] iPhone 16 128GB 256GB 512GB 各色 スマホ 本体view page

【二次方程式の利用】動点の文章問題の解き方の4つのステップ view page

電波通信 不動点定理 view page

バナッハの不動点定理（縮小写像の原理）｜証明と応用例も紹介 view page

【中古】iPhone 14 128GB 256GB 512GB A2881 スマホ スマートフォン 本体 SIMフリー ミッドナイト (PRODUCT)RED スターライト パープル ブルー…view page

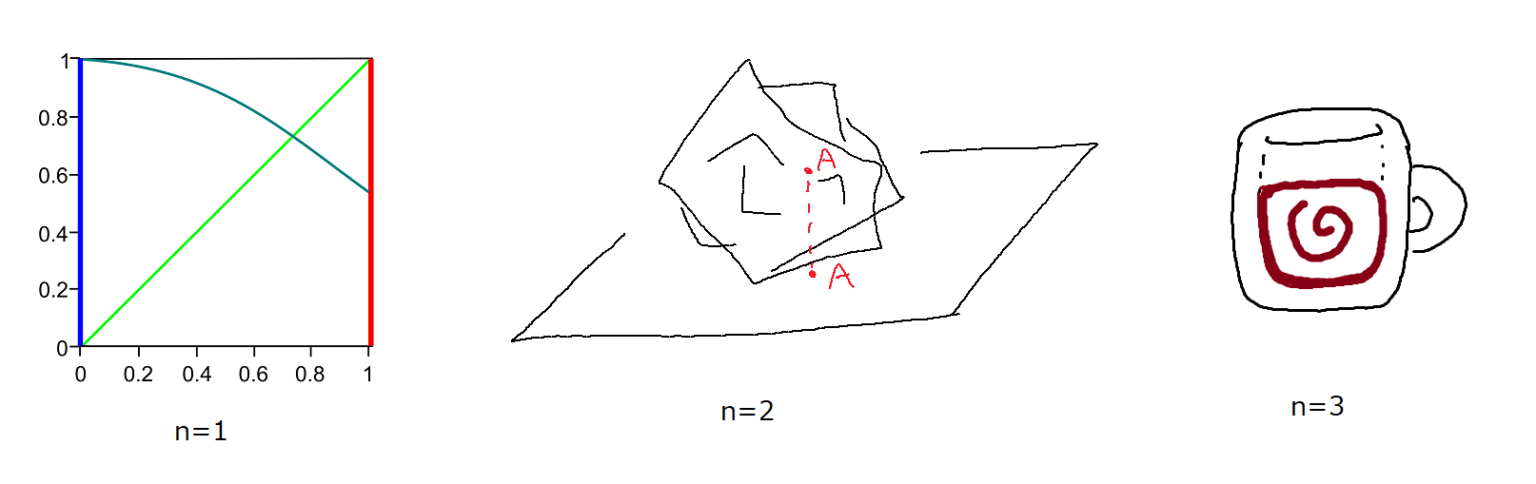
マスログトポロジー有名定理その１～ブラウワーの不動点定理～【数学×アート】数式を使って「面白い曲線」を描きたい第2弾~円の...やさしく学ぶ統計学～試行と事象とは？～やさしく学ぶ統計学～重複組み合わせとは？～大人が学ぶ算数 ―和・差・積・商って？計算の順序ときまり...78×72は？2桁の掛け算を一瞬で計算できる確率を上げる...革命的掛け算（2桁×2桁）のやり方を伝授します【インド式...「Web担当者Forumミーティング2022春」にて代表堀口が講...数学とデザインにおける大人の学びを考える【ニューメラシートークラ...【展示会情報】「青の四つ巴展」が代官山で開催！ view page

身勝手な主張 view page

Yahoo!知恵袋不静定の反力の求め方 view page

【国内版SIMフリー・新品未開封/未使用品】 iPhone16 128GB 256GB 512GB 各色 スマホ 本体view page

三平方の定理 図形の折り返し - 中学数学 練習問題プリント 数奇な数 view page

SUSHITEMPLEのブログ Schauderの不動点定理について view page

不動点定理 view page

【中古】iPhone SE 第3世代 2022 SE3 A2782 64GB 128GB スマホ スマートフォン SE3 本体 SIMフリー ミッドナイト レッド スターライト docomo au…view page

三石・数学塾 view page

【2016年】北海道公立高校入試過去問「数学」（標準・裁量問題）を画像で解説！ view page

Banachの不動点定理とその周辺 view page

【19日20時からポイントUP! 大感謝祭】新品未開封品【Nランク】SIMフリー iPhone17 Pro 256GB Apple シルバー MG854J/A コズミックオレンジ MG864J/A…view page

スクリーンショット 2021-02-21 12.38.20 view page

ブラウアーの不動点定理 view page

不動点定理（読み）ふどうてんていり view page

iPhone 16e simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン 【ご注文から30分経過後はキャンセル不可】【自宅受け取り限定…view page

書記が数学やるだけ#618 離散量の不動点定理，ボルスク・ウラムの定理 view page

離散量の不動点定理【1973年度 名古屋大学ほか】 view page

Spanの意味とは【線形結合】 view page

【19日20時からポイントUP! 大感謝祭】新品未開封品【Nランク】SIMフリー iPhone16e 128GB Apple A3409 ブラック ホワイト MD1Q4J/A MD1R4J/A…view page

ベクトル場のゼロ点の存在 view page

エンジニアを目指す浪人のブログ 制約なし凸最適化問題に対するニュートン法の，目的関数に強凸性，そのヘッセ行列にリプシッツ連続性を仮定するときの収束解析をまとめる view page

マスマスマズマズ研究ノート view page

純正バッテリー100%｜90%【中古】iPhone 15 128GB 256GB 512GB A3089 スマホ スマートフォン 本体 SIMフリー ピンク イエロー グリーン ブルー ブラック…view page

電気磁気工学を学ぶ view page

スクリーンショット 2021-02-26 7.46.04 view page

一般の線形空間 view page

iPhone 15 simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォンview page

f:id:meisei-gakuin:20190521224906j:plain view page

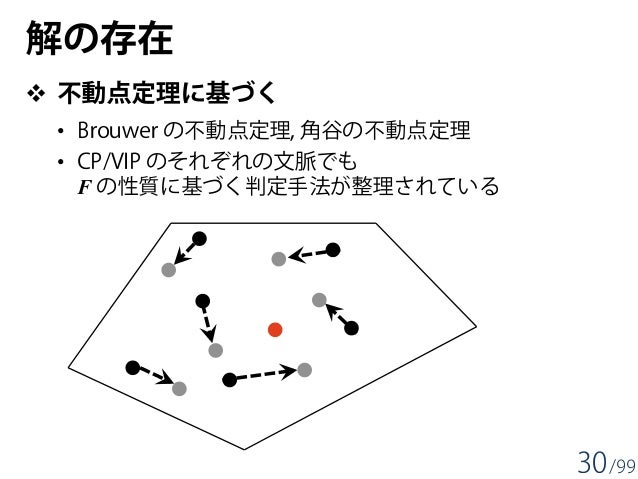
均衡問題の数理解析: 解の存在, 一意性, 安定性, 分岐 均衡問題の数理解析: 解の存在, 一意性, 安定性, 分岐 view page

一次関数の利用　動点の問題 view page

iPhone 17 Pro Max 端末本体のみ(機種変更はこちら) SIMフリー 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン…view page

不動点×不動点×不動点コンビネータ 不動点×不動点×不動点コンビネータ view page

ざっくりとハフ変換を理解する view page

不動点×不動点×不動点コンビネータ 不動点×不動点×不動点コンビネータ view page

【19日20時からポイントUP! 大感謝祭】新品未開封品【Nランク】SIMフリー iPhone17 256GB ブラック MG674J/A ホワイト MG684J/A ミストブルー…view page

バナッハの不動点定理(縮小写像の原理)とその証明 view page

働きアリ アリ view page

はじパタ6章前半はじパタ6章前半 view page

【中古】iPhone SE 第2世代 2020 SE2 A2296 64GB 128GB 256GB スマホ スマートフォン SE2 本体 SIMフリー ブラック レッド ホワイト docomo…view page

第5回 2011年5月27日ロトカ・ヴォルテラ方程式 view page

第3回 2010年4月23日個体成長とカオスロトカ・ヴォルテラ方程式 view page

f:id:kenkitube:20160125140538p:plain view page

純正バッテリー100%｜90%【中古】iPhone 14 Pro Max 128GB 256GB 512GB 1TB スマホ スマートフォン 本体 SIMフリー ブラック ゴールド シルバー…view page

補題 png view page