Images of 分立
![[P5倍 本日 12時〜] 加湿器 ＜4年連続ランキング1位＞ [1年保証] W除菌で特許取得 UV除菌機能付き加湿器 ハイブリッド加湿器 上から給水 おしゃれ 約100℃加熱 ぬめり防止 熱でかび予防 上部給水式加湿器 アロマ 卓上 節電](https://thumbnail.image.rakuten.co.jp/@0_mall/dondon/cabinet/jxh003j_8.jpg?_ex=300x300)
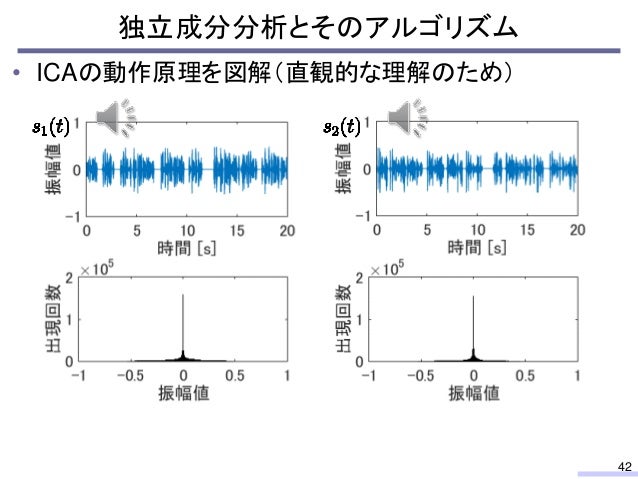
音響メディア信号処理における独立成分分析の発展と応用, History of independent component analysis for sound media signal processing and its applications音響メディア信号処理における独立成分分析の発展と応用, History of independent component analysis for sound media signal processing and its applications
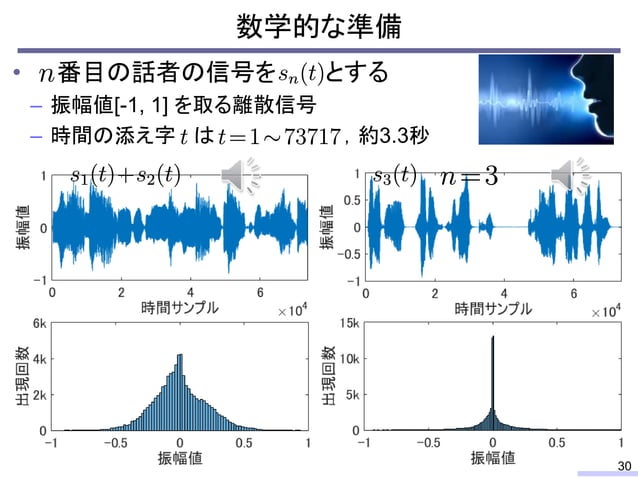
音響メディア信号処理における独立成分分析の発展と応用, History of independent component analysis for sound media signal processing and its applications音響メディア信号処理における独立成分分析の発展と応用, History of independent component analysis for sound media signal processing and its applications
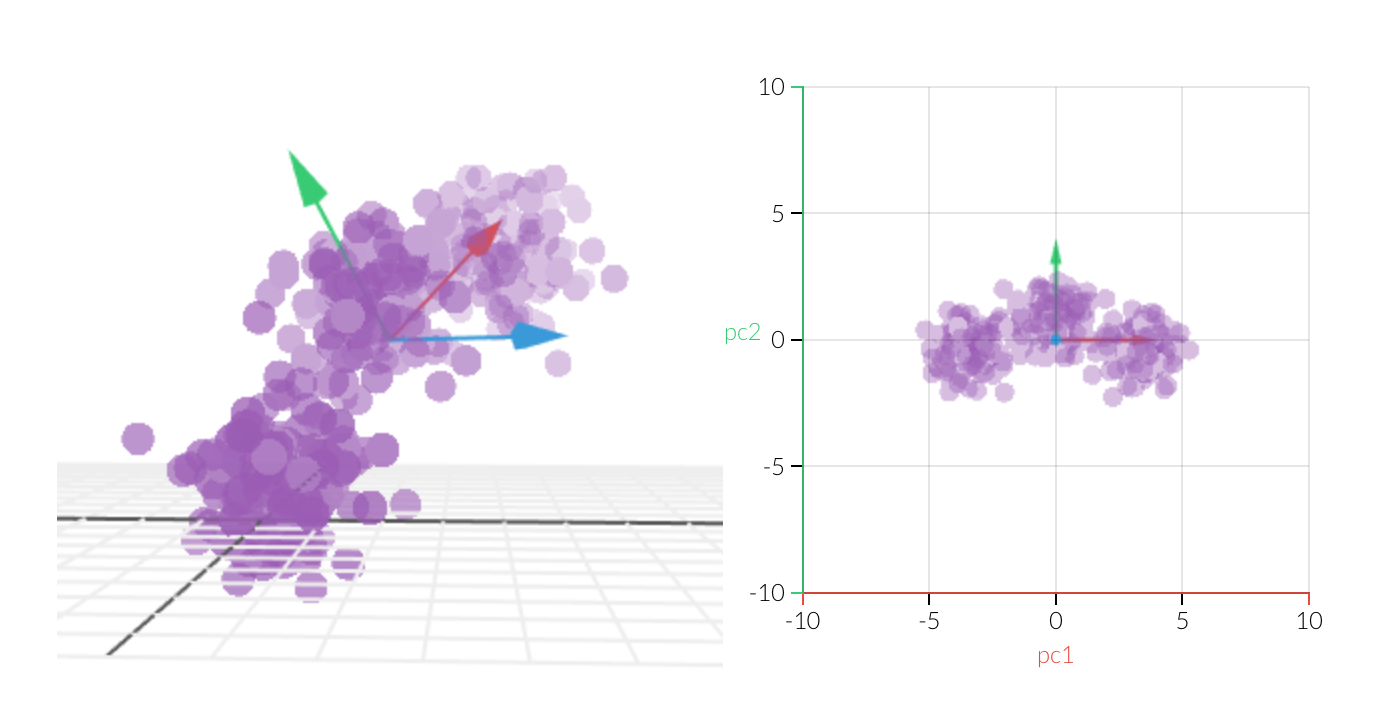
主成分分析 独立成分分析_主成分分析说明\r\n \r\n 发布时间：2020-09-06\r\n PYTHON\r\n JAVA\r\n 算法\r\n MYSQL\r\n 数据分析\r\n \r\n \r\n \r\n \n 主成分分析 独立成分分析\n \n \n \n \n Principal Components Analysis (PCA) is one of the most famous algorithms in Machine Learning (ML), it aims to reduce the dimensionality of your data or to perform unsupervised clustering. PCA is undoubtedly used worldwide 🌍, in any fields that manipulate data, from finance to biology.\n P rincipal成分分析(PCA)是机器学习(ML)最著名的算法之一，其目的是减少数据的维度或执行无监督聚类 。 毫无疑问，PCA已在全球范围🌍应用于从金融到生物学的任何可操纵数据的领域。 \n While there are many great resources that give the recipe to perform PCA or nice spatial interpretation of what it does, there are few that goes under the hood of the mathematical concepts behind it.\n 尽管有很多很棒的资源可以使食谱执行PCA或对其功能进行很好的空间解释，但是背后的数学概念却很少。 \n Although it is not necessary to understand the maths to use the PCA out of the box, I strongly believe that a deep understanding of the algorithms makes you a better user, able to understand its performance and drawbacks in any specific situations. Besides, mathematical concepts are interconnected in ML and understanding PCA may help you get on with other ML notion that uses algebra (for the curious, check Figure 3. in the post-scriptum section at the end of the post).\n 尽管无需开箱即用地使用PCA来理解数学，但我坚信对算法的深入了解可以使您成为更好的用户，并能够理解其在任何特定情况下的性能和缺点。 此外，数学概念在ML中是相互联系的，对PCA的理解可以帮助您与其他使用代数的ML概念融为一体(出于好奇，请查看文章末尾的后文部分中的图3)。 \n This post attempts to explain the different steps with the mathematical concepts behind it. I assume the reader is already familiar with algebra fundamentals.\n 这篇文章试图用其背后的数学概念来解释不同的步骤。 我认为读者已经熟悉代数基础知识。 \n \n \n \n \n \n \n First things first, let’s recap the PCA recipe for a quick refresh of the different involved steps:\n 首先，让我们回顾一下PCA配方，以快速刷新所涉及的不同步骤： \n Normalize your data, let’s call the normalized dataset X. X has N rows (examples) and d columns (dimensions), it is a (N, d) matrix 标准化数据，我们称其为标准化数据集X。 X具有N行(示例)和d列(维度)，它是(N，d)矩阵 Compute the covariance matrix Σ of X 计算X的协方差矩阵Σ Compute the covariance matrix Σ of XΣ is a (d, d) matrix 计算XΣ的协方差矩阵Σ是(d，d)矩阵 Compute the eigenvectors and eigenvalues of Σ 计算Σ的特征向量和特征值 Sort the k eigenvectors with largest eigenvalues (these are the k principal components) and make W, which is a (d, k) matrix 对具有最大特征值的k个特征向量(这些是k个主成分)进行排序，并令W为一个(d，k)矩阵 Project the original dataset X on the lower dimension space made from the k eigenvectors sorted from step 4, which is W 将原始数据集X投影到由步骤4排序的k个特征向量组成的低维空间上，即W Project the original dataset X on the lower dimension space made from the k eigenvectors sorted from step 4, which is WX’ = XW…… X’ is ready👨🍳 ! X’ is now a (N, k) matrix 将原始数据集X投影到由步骤4排序的k个特征向量组成的低维空间上，即W X'= XW …… X'准备就绪！ X'现在是一个(N，k)矩阵 \n Given that k<
Dictionary
Japanese
分立Reading
ぶんりつEnglish
noun or participle which takes the aux. verb suru
- segregation
- separation
- independence