Images of 基底関数

基底変換行列 基底変換行列 view page

【新登場】iPhone 16e simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン…view page

f:id:Parco1021:20200206165132p:plain view page

Image from Gyazo view page

Figure JPOXMLDOC01-appb-M000024 view page

【エントリーで更にポイント10倍！】【中古】iPhone SE 3 第3世代 2022 A2782 64GB 128GB スマホ スマートフォン SE3 本体 SIMフリー ミッドナイト レッド…view page

Yahoo!知恵袋線形代数の基底変換行列に関する質問です。 基底aからbへの変換行列と言われれば、b=という形にすると思うのですが、画像のようにa=としてる教科書を見つけました。 どっちが正しいのでしょ view page

Prml6 Prml6 view page

動径基底関数、RBFカーネル、およびRBFネットワークを簡単に説明 view page

【エントリーで更にポイント10倍！】【中古】iPhone 14 128GB 256GB 512GB A2881 スマホ スマートフォン 本体 SIMフリー ミッドナイト (PRODUCT)RED…view page

PRMLの線形回帰モデル（線形基底関数モデル）PRMLの線形回帰モデル（線形基底関数モデル） view page

動径基底関数（RBF） view page

f:id:shirakonotempura:20190315044045p:plain view page

【エントリーで更にポイント10倍！】【中古】iPhone 14 Pro 128GB 256GB 512GB 1TB A2889 スマホ スマートフォン 本体 SIMフリー ブラック ゴールド…view page

ラビット・チャレンジ（機械学習レポート）１．線形回帰モデル２．非線形回帰モデル３．ロジスティック回帰モデル４．主成分分析（PCA）５．アルゴリズム６．サポートベクターマシーン（SVM） view page

基底関数の集合に対応するカーネル関数の計算とPythonを用いたグラフの作成 view page

8. MARS の基底関数 (BF: basis functions) view page

iPhone 16 Pro simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン…view page

f:id:Zellij:20121019001213p:image view page

富山de居合　『無涯塾日記』 そらお view page

基底関数系の概要 view page

【4日20時からポイントUP! スーパーSALE】新品未開封品【Nランク】SIMフリー iPhone16 Plus 256GB Apple A3289 ブラック ホワイト ピンク ウルトラマリン…view page

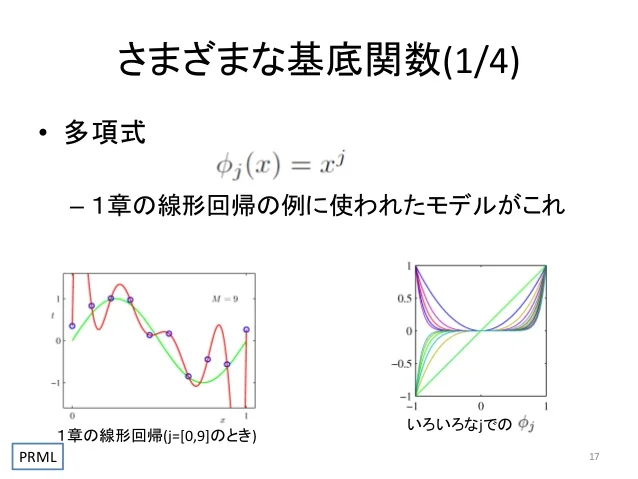
PRMLの線形回帰モデル（線形基底関数モデル）PRMLの線形回帰モデル（線形基底関数モデル） view page

「3.1.2最小二乗法の幾何学」PRML勉強会4 @筑波大学 #prml学ぼう 「3.1.2最小二乗法の幾何学」PRML勉強会4 @筑波大学 #prml学ぼう view page

PC CHEM BASICS.COM 基底関数はどれを選べばいいの？ コメント view page

【4日20時からポイントUP! スーパーSALE】新品未開封品【Nランク】SIMフリー iPhone16 256GB Apple A3286 ブラック ホワイト ピンク ウルトラマリン ティール【…view page

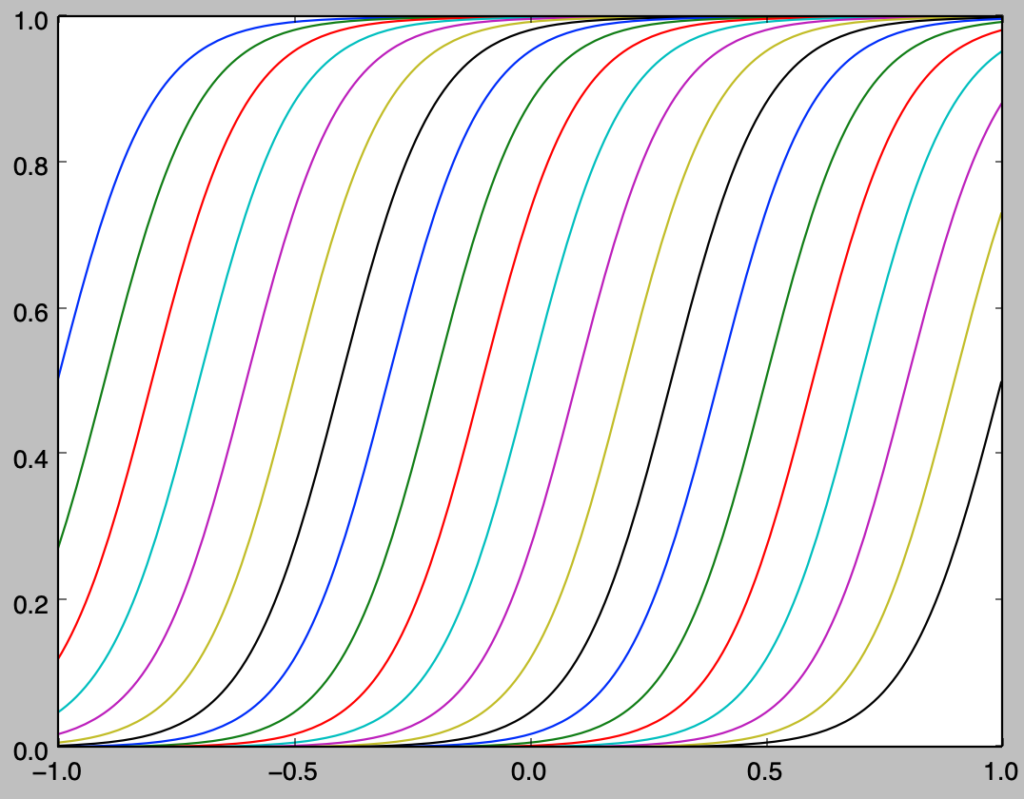
基底関数の集合に対応するカーネル関数の計算とPythonを用いたグラフの作成 view page

密度比推定による異常検知 view page

【機械学習入門】実験データの解析に役立つ非線形回帰分析を利用してみよう本記事の概要目次1. 非線形回帰の概要2. データの作成3. モデルの作成4. 正則化法5. おわりに機械学習入門のリンク view page

【新登場】iPhone 16e simフリー 国内正規品 Apple 本体 端末 新品 回線セット（18歳未満の購入不可） 純正 認定店 楽天モバイル公式…view page

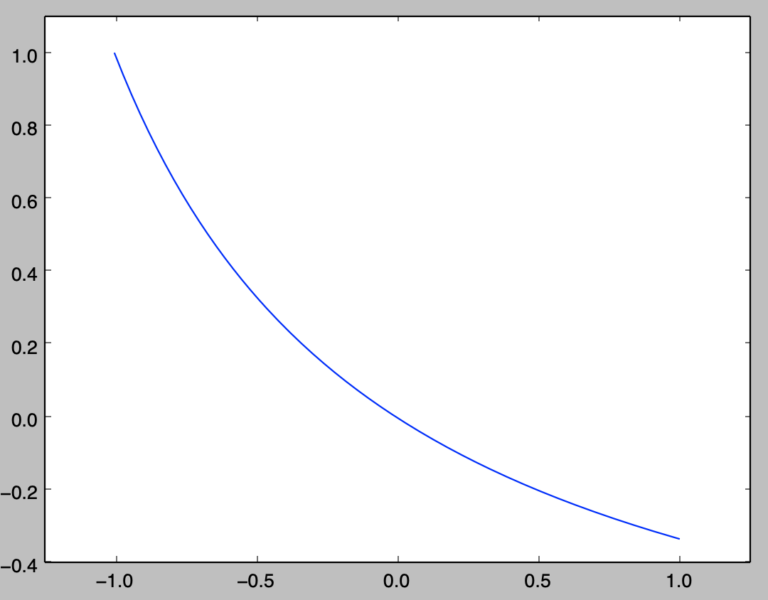
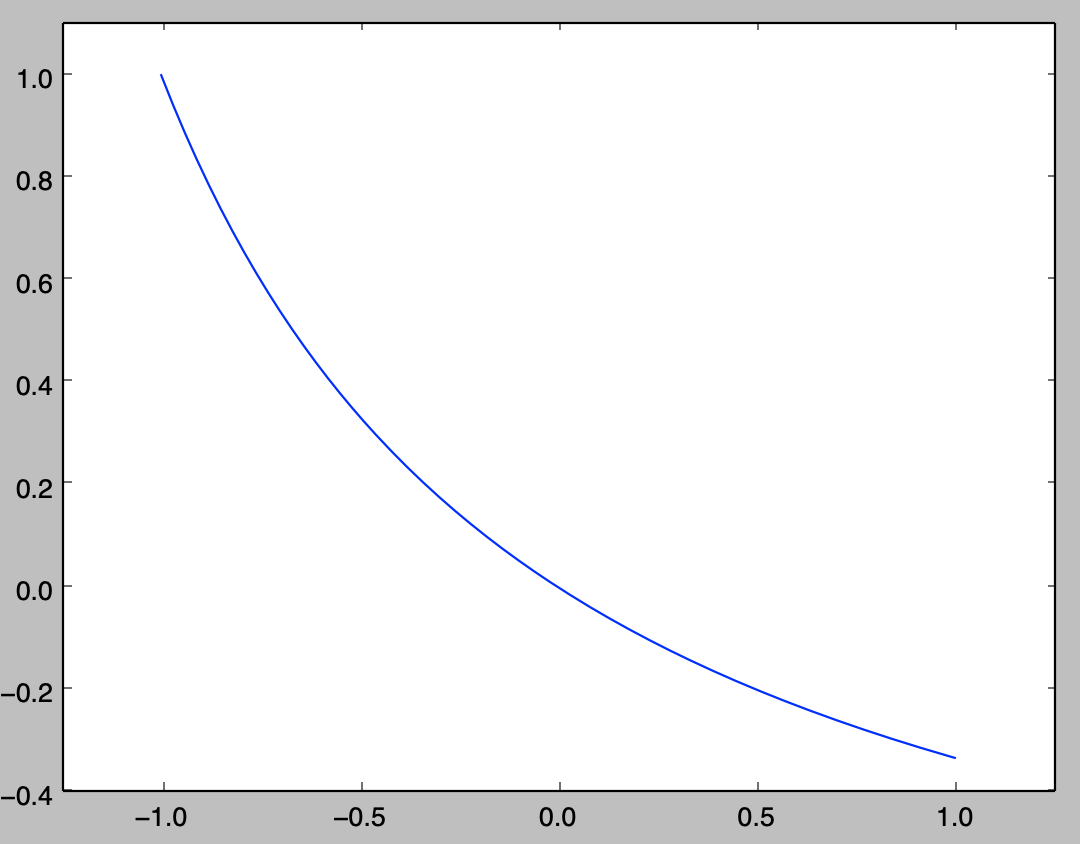
基底関数の集合に対応するカーネル関数の計算とPythonを用いたグラフの作成 view page

f:id:Parco1021:20200206165016p:plain view page

bernstein view page

[新品未開封｜SIMフリー] iPhone 16 128GB 256GB 512GB 各色 スマホ 本体view page

基底関数系の概要 view page

VQEは既存の量子化学計算を超えるだろうか？ ～精度と計算リソースの見積もり～ TL;DR書誌情報用語の整理手法分子のエネルギー計算化学反応エネルギーまとめVQEは既存の量子化学計算を超えるか？という問いに対して view page

応用数学、機械学習、深層学習:前編 1 応用数学　機械学習　深層学習: Day1確認テストの考察中間層出力演習結果と考察 view page

【エントリーで更にポイント10倍！】【中古】iPhone 13 mini 128GB 256GB 512GB A2626 スマホ スマートフォン 本体 SIMフリー グリーン ピンク ブルー…view page

「関数データエクスプローラ」の例 view page

アト秒レーザーで位相を分けた電子波動関数の直接イメージングに成功アト秒レーザーで位相を分けた電子波動関数の直接イメージングに成功 view page

PRMLの線形回帰モデル（線形基底関数モデル）PRMLの線形回帰モデル（線形基底関数モデル） view page

iPhone 16 simフリー 端末本体のみ（機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン 【ご注文から30分経過後はキャンセル不可】【自宅受け取り限定 /…view page

プログラマのための放射基底関数ネットワーク view page

f:id:wantanBlog:20200215011308p:plain view page

PC CHEM BASICS.COM BSSE(基底関数重なり誤差)について知ろう コメント view page

【エントリーで更にポイント10倍！】【中古】iPhone 13 Pro 128GB 256GB 512GB 1TB A2636 スマホ スマートフォン 本体 SIMフリー アルパイルグリーン…view page

基底 (basis)と次元（dimension） view page

<科目> 機械学習　第二章:非線形回帰モデル<科目> 機械学習 view page

CMSI計算科学技術特論B(9) オーダーN法2 view page

[新品未開封｜未使用品｜SIMフリー] iPhone 15 128GB 256GB 各色 スマホ 本体view page

PRML第６章「カーネル法」 view page

動径基底関数、RBFカーネル、およびRBFネットワークを簡単に説明 view page