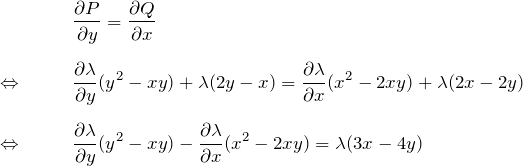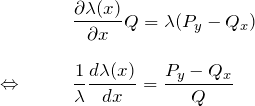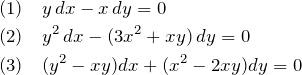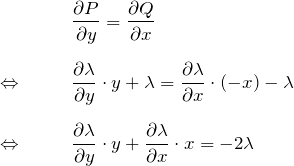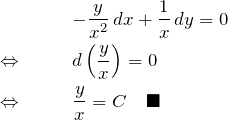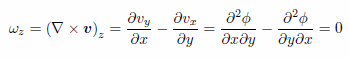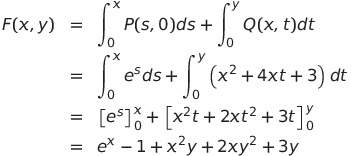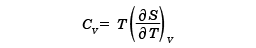【クーポン&ポイント10倍】お歳暮 冬ギフト プレゼント ギフト クリスマス 2025 百貨店で人気 お菓子 【パティスリーキハチ 公式】 人気 おしゃれ 高級 ギフト ランキング 洋菓子 内祝い…

【スーパーSALE限定★61%OFF!】 電動自転車 a01 折りたたみ 電動アシスト自転車 erway 自転車 電気自転車 パワフル 5段階アシスト搭載 20インチ 7段変速 おしゃれ スポーツ…

【無料★特典付】 【特別価格】水受けセット ユニソン スプレスタンド60ソリッド 蛇口1個セット+ステンレスパン 蛇口付き立水栓 水栓柱&ガーデンパン 組合せセット 4カラー 1口水栓柱…
Sample Scripts from GB Books GB011: 2次元の完全流体

【LINE追加で最大2000円OFF】 ガスコンロ リンナイ ガステーブル パールクリスタル ホワイト 白 59cm 両面焼きグリル プロパン 都市ガス 据置型ガスコンロ 2口…
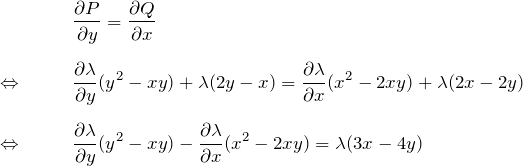
\begin{eqnarray*} &&\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\\\\ \Leftrightarrow \quad&& \frac{\partial \lambda }{\partial y }(y^2 -xy)+ \lambda(2y-x)= \frac{\partial \lambda }{\partial x}(x^2-2xy)+\lambda(2x-2y)\\\\ \Leftrightarrow \quad&& \frac{\partial \lambda}{\partial y}(y^2 -xy)- \frac{\partial \lambda}{\partial x}(x^2-2xy) =\lambda(3x-4y) \end{eqnarray*}

【スーパーSALE限定★64%OFF~!】 サスペンション搭載 型式認定済 電動自転車 免許不要 130km走行可能 a02 折りたたみ 電動アシスト自転車 20インチ 自転車 350Wモーター…

f:id:queesmrg:20191027191449j:plain

期間値引クーポンあり ドレッサー おしゃれ 女優ミラー《自社製品》可愛い デスク 欧風 鏡台 お姫系 ベロア調 テーブル 幅80cm 幅60cm 幅100cm チェスト スツール LEDミラー…

f:id:queesmrg:20191027192249j:plain

【全品半額クーポン配布中☆先着500名|4日20時から】 iphone16 ケース iphone15 ケース スマホケース カード iphone14 ケース iphone13 ケース…
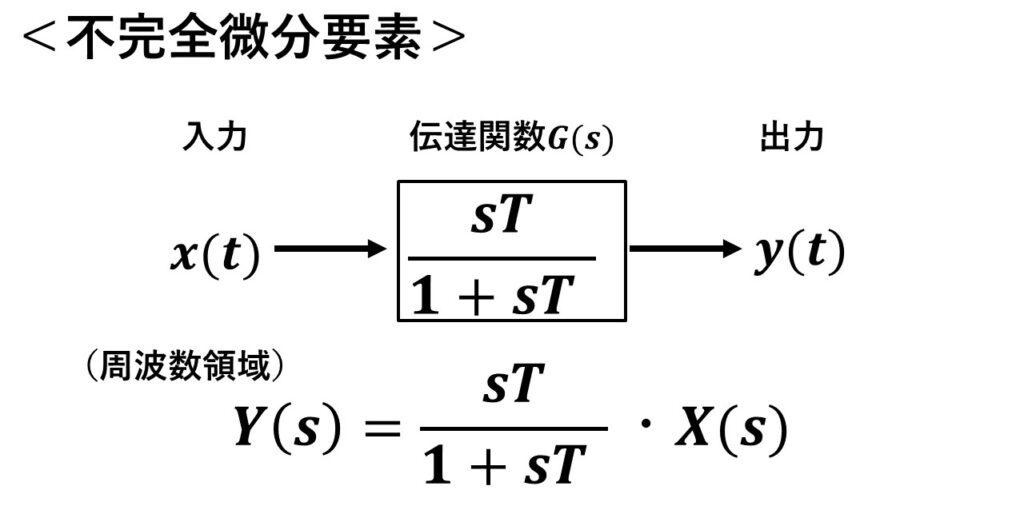
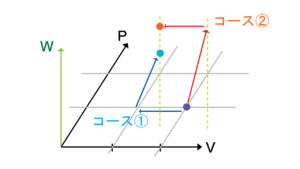
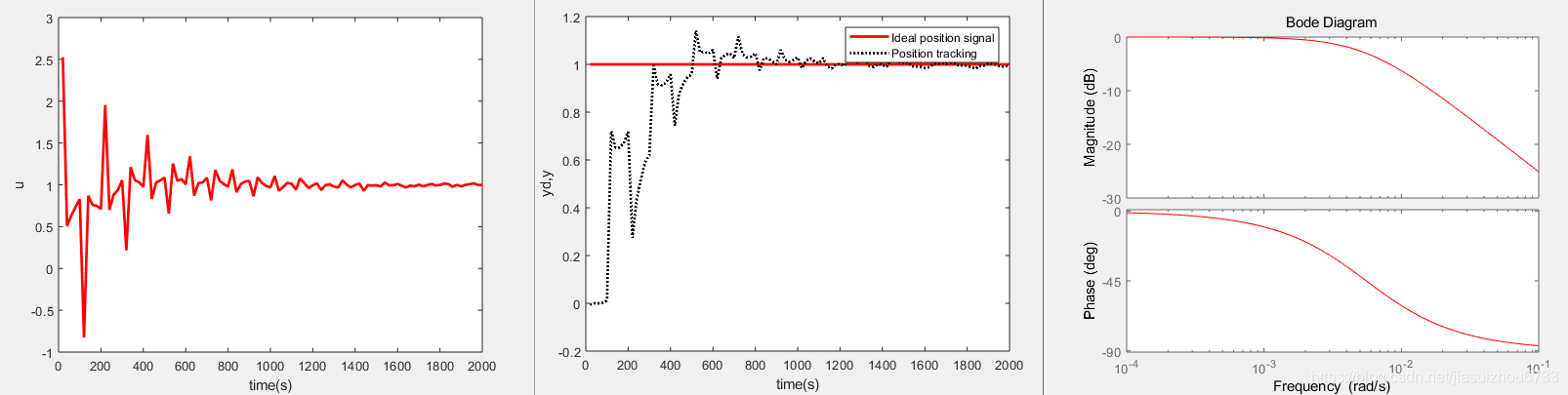
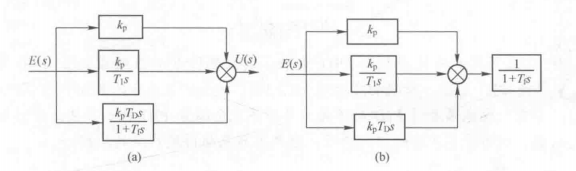
基本的な伝達関数のステップ応答とボード線図について分かりやすく解説 ー不完全微分,一次進み遅れ(位相進み遅れ補償)ー
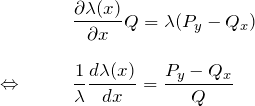
\begin{eqnarray*} &&\frac{\partial \lambda (x)}{\partial x}Q=\lambda(P_y -Q_x)\\\\ \Leftrightarrow \quad&& \frac{1}{\lambda}\frac{d\lambda (x)}{dx}=\frac{P_y-Q_x}{Q} \end{eqnarray*}

【納期お問合せ下さい】 UNISON ガーデンシンク バル 立水栓 バルスタンド トールポット 上下蛇口 セット BARU 水栓柱 ユニソン 補助蛇口 ホース用 2口 ガーデンポット サテン…

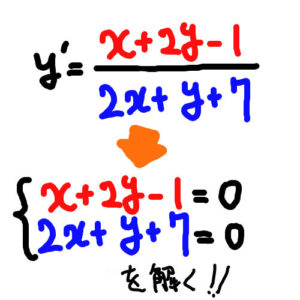
微分方程(x^2-y)dx-(x-y)dy=0的通解微分方程(x^2-y)dx-(x-y)dy=0的通解10

応接セット 4点セット 4人 応接 ソファ 椅子 応接テーブル ソファセット 応接室 おしゃれ モダン 会議セット 商談 オフィス コンパクト シャルマン SA681-2-T13S
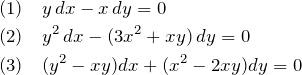
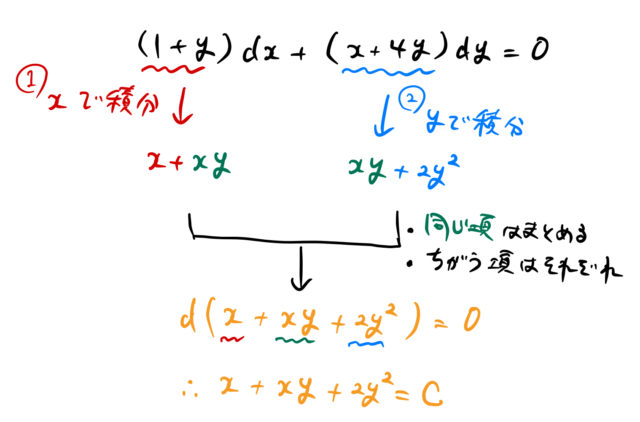
\begin{eqnarray*} &&(1)\quad y\,dx-x\,dy=0\\ &&(2)\quad y^2\,dx-(3x^2+xy)\,dy=0\\ &&(3)\quad (y^2-xy)dx+(x^2-2xy)dy=0 \end{eqnarray*}

ACTUS カタログギフト<SHINRIN(森林)> 内祝い 結婚祝い 結婚内祝い 出産祝い 引き出物 カタログ ギフト グルメ おしゃれ 結婚 内祝 引出物 引越し祝い 引っ越し 新築祝い…

f:id:masato19641105:20200617011206j:image

\スーパーSALE限定50%OFF/【5年保証】シーリングライト LED 三色切替 6灯 8灯 6畳 8畳 10畳 12畳 北欧 E26 リビング 照明 おしゃれ 回転可能 スポットライト…
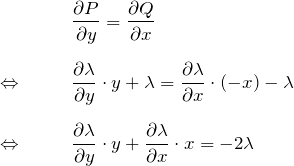
\begin{eqnarray*} &&\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\\\\ \Leftrightarrow \quad&& \frac{\partial \lambda}{\partial y}\cdot y + \lambda = \frac{\partial \lambda}{\partial x}\cdot(-x)-\lambda\\\\ \Leftrightarrow \quad&& \frac{\partial \lambda}{\partial y}\cdot y + \frac{\partial \lambda}{\partial x}\cdot x=-2\lambda \end{eqnarray*}
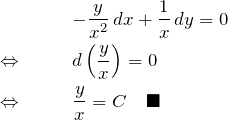
\begin{eqnarray*} &&-\frac{y}{x^2}\,dx+\frac{1}{x}\,dy=0\\ \Leftrightarrow \quad&&d\left(\frac{y}{x}\right)=0\\ \Leftrightarrow \quad&&\frac{y}{x}=C\quad\blacksquare \end{eqnarray*}

お歳暮 お菓子 ギフト スイーツ クッキー 詰め合わせ 御歳暮 冬ギフト 高級 おしゃれ 誕生日プレゼント 個包装 がらんの小石 30個入 お取り寄せスイーツ プチギフト 焼き菓子 出産祝い…
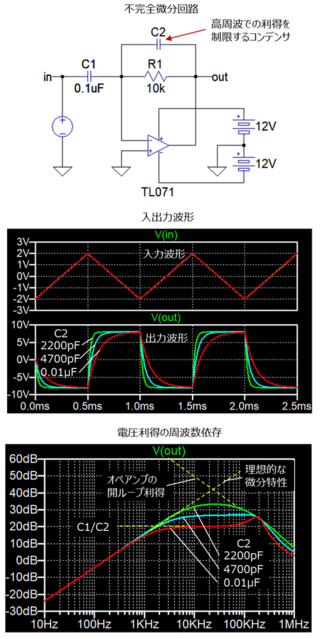
Yahoo!知恵袋オペアンプについての質問です. 先日オペアンプを使った実験を行ったのですが,
1. オペアンプの飽和特性での最大(+11.5V)最小(-10.0V)が, 電源電圧の±12Vに届きませんでした.
2. 反転

基本的な伝達関数のステップ応答とボード線図について分かりやすく解説 ー不完全微分,一次進み遅れ(位相進み遅れ補償)ー

\スーパーSALE限定50%OFF/シーリングライト 照明器具 LED 調光調色 おしゃれ 電気 北欧 照明 6畳 8畳 10畳 12畳 14畳 リモコン付き LED対応 インテリア 間接照明…