Images of 実数空間

P3161697.JPG view page

【LINE500円OFFクーポン】 枕 枕カバー 付 ヒツジのいらない枕 ギフト 実用的 健康グッズ 誕生日 ギフト 洗える 通気性 寝用枕 うつぶせ寝 まくら ジェル 首 寝返り 横向き 仰向け…view page

f:id:ogyahogya:20140919110412p:plain view page

SUUGAKU.JP view page

サイエンスアゴラ研究100連発 〜目に見えて楽しい数学〜サイエンスアゴラ研究100連発 〜目に見えて楽しい数学〜 view page

【新商品】 NERUS ふわとろ毛布 Air AirPremium 【正規品】 毛布 ブランケット もこもこ毛布 モコモコ とろとろ ふわふわ シングル セミダブル ダブル ハーフ ふわもこ…view page

位相空間論-No.1:距離空間 view page

数空間\(R^n\) view page

基礎的な概念 view page

【“5年連続”インテ寝具総合1位】確かな品質 ｢純｣ 高反発(R) 〈全部洗える〉 マットレス 10cm厚 3つ折り メッシュ/パイル 折りたたみ ベッドマットレス 10cm セミシングル…view page

2変数関数と偏微分、勾配：グラフ、接平面を描いてみよう view page

SUUGAKU.JP view page

SUUGAKU.JP view page

【LINE登録で300円クーポン】【一部カラー20％引！】 販売累計12.9万枚！ ラグ 洗える シエロ ラグマット キルトラグ 絨毯 北欧 おしゃれ くすみ カーペット 95×130…view page

\mathbb{Q}(x) = \{ f(x)/g(x) \mid f(x),g(x) \in \mathbb{Q}[x], g(x) \neq 0 \} view page

\mathbb{R}(x) = \{ f(x)/g(x) \mid f(x),g(x) \in \mathbb{R}[x], g(x) \neq 0 \} view page

Tokyo.R #96 theory of probability view page

【50%オフクーポン】即納 収納ボックス 収納ケース 折りたたみ 収納 ふた付き キャスター付き 5面開き 前開き 27L 40L 53L 82L 屋外 おしゃれ プラスチック 衣装ケース…view page

SUUGAKU.JP view page

収束数列と有界数列の関係 view page

空間ベクトルの要点 view page

【5の倍数日P5倍】マットレス 線径2.3mmのエッジサポート ポケットコイル シングル セミダブル ダブル 85スモールシングル セミシングル 厚さ20cm 配送日指定可 送料無料…view page

Tokyo.R#79 BeginneRSession-確率の基礎 view page

4.4 ベクトル空間の基と次元 view page

画面1　実数計算の場合は結果が「5.0」 view page

ラグ 洗える 1畳 1.5畳 2畳 3畳 4畳 洗えるラグ おしゃれ 北欧 防ダニ 冬 床暖房対応 オールシーズン 滑り止め マット ラグマット カーペット ラグカーペット センターラグ 正方形…view page

SUUGAKU.JP view page

SUUGAKU.JP view page

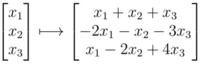
Yahoo!知恵袋線形写像の問題です！2次元実数空間から1次元空間への写像T1が線形写像か理由も踏まえて答えろという問題です。写真のやり方で大丈夫でしょうか？ view page

【SNSで話題/意匠権取得】 天板つき スラックスハンガー 10本 15本 20本掛け コンパクト スリム パンツラック ズボンハンガー パンツハンガー 衣類 収納 タオルハンガー…view page

怜悧玲瓏　～高校数学を天空から俯瞰する～ 十六夜♪ view page

SUUGAKU.JP view page

内積（読み）ないせき view page

【10％OFF】 Yogibo Mega Moon Pillow（ヨギボー メガ ムーン ピロー） ゆるやかな三日月カーブで包み込む。枕から背もたれ、足枕まで大活躍 【 ビーズクッション…view page

ユークリッド空間の定義 view page

SUUGAKU.JP view page

抽象ベクトル空間・線形空間の具体例R^N：順序対と直積集合 view page

ひな暖ぬくぬくセット （毛布＋敷きパッド） シングル セミダブル ダブル クイーン【ひな暖 ひなだん ひな壇 保温 マットレス用 ふとん用 暖かい毛布 洗える 布団 冬 あったか毛布…view page

image view page

位相空間論-No.1:距離空間 view page

image view page

[P20倍／28日まで] [レビュー11000件超え／高評価4.59点] 毛布 シングル 140×200cm ブランケット 冬 ひざ掛け 膝掛け 掛け毛布 160×200cm 180×200cm…view page

モンテカルロ シミュレーション view page

確率的手法とコーシー・シュワルツ不等式によるグラフのTuránの定理 前書き短い回り道：ユークリッド空間のコーシーシュワルツ不等式Turánの定理の証明Turánの定理の堅さ view page

空間ベクトル view page

《予約販売》【日本No.1受賞】ハグモッチ 正規品【さらに改善】【医師の92%推奨】30万人の眠りを変えた 枕 ふわもち 腰 肩 首 いびき防止 抱き枕 妊婦 誕生日プレゼント 人をダメにする…view page

中学数学　一次関数 view page

２変数の関数と極限の考え方 view page

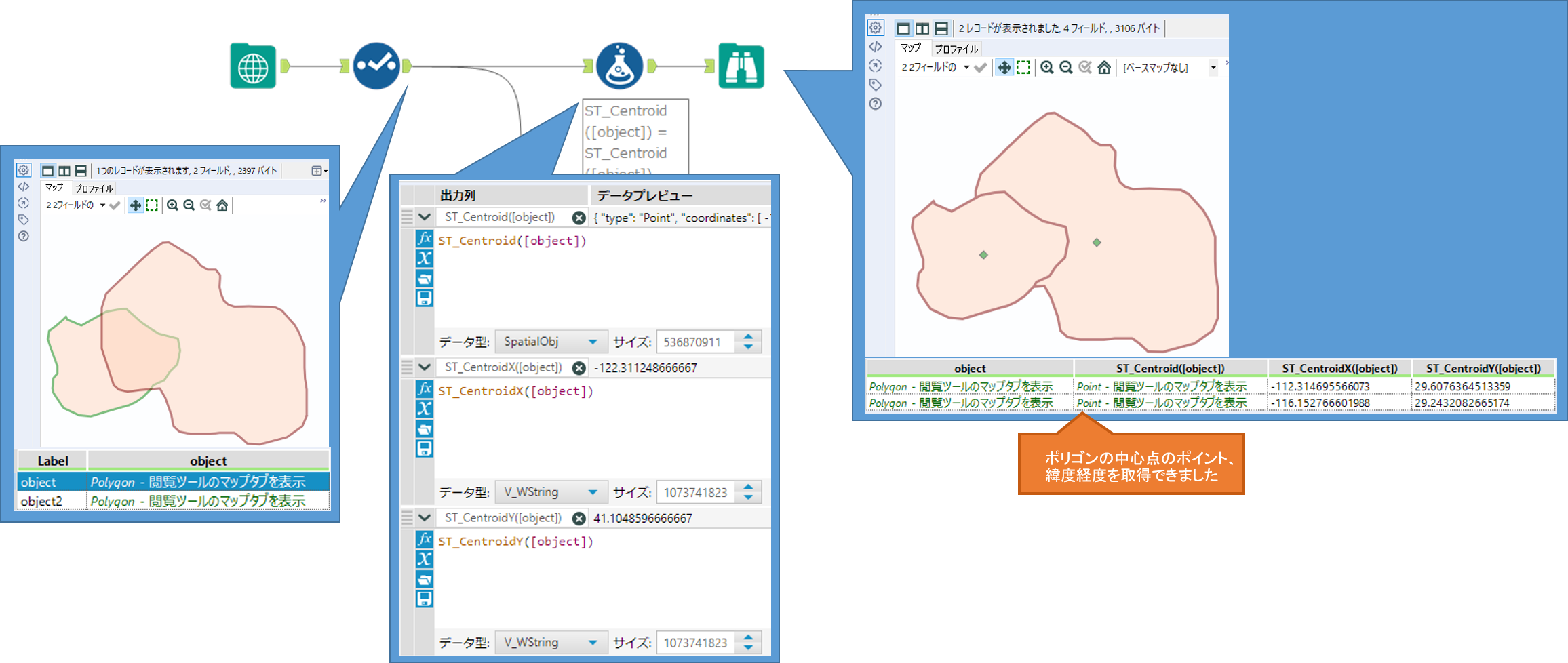
【Alteryx関数シリーズ】空間関数の使い方Alteryxで使用できる関数の「空間関数」の使い方をご紹介します view page

2大特典［ 分別ダストワゴン タワー / 蓋付き / 目隠し / 2分別 / 3分別 / 45L ］山崎実業 tower キッチン ゴミ箱 ごみ箱 ダストボックス ゴミ袋ハンガー フタ付き ふた…view page

怜悧玲瓏　～高校数学を天空から俯瞰する～ 十六夜♪ view page

標準基底 view page