![数次相続・代襲相続をめぐる実務ー相続人・相続分の確定ー【電子書籍】[ 中込一洋 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/9339/2000012649339.jpg?_ex=300x300)
数次相続・代襲相続をめぐる実務ー相続人・相続分の確定ー【電子書籍】[ 中込一洋 ]
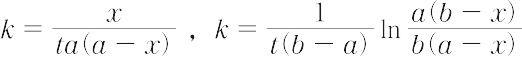
二次反応(読み)にじはんのう(英語表記)second-order reaction
![数次相続・代襲相続をめぐる実務ー相続人・相続分の確定ー [ 中込 一洋 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/0921/9784788290921_1_2.jpg?_ex=300x300)
数次相続・代襲相続をめぐる実務ー相続人・相続分の確定ー [ 中込 一洋 ]
![代襲相続・再転相続・数次相続の法律と実務[本/雑誌] / 安達敏男/著 吉川樹士/著](https://thumbnail.image.rakuten.co.jp/@0_mall/neowing-r/cabinet/item_img_2030/neobk-2799082.jpg?_ex=300x300)
代襲相続・再転相続・数次相続の法律と実務[本/雑誌] / 安達敏男/著 吉川樹士/著

f:id:ssr-yuki:20181206225158p:plain

代襲相続・再転相続・数次相続の法律と実務/安達敏男/吉川樹士【3000円以上送料無料】

技術士(機械)一次試験直近の過去問解説2今回は平成29年Ⅲ-12それでは問題です。

代襲相続・再転相続・数次相続の法律と実務/安達,敏男 吉川,樹士 日本加除出版

ALBERT Official BlogGraph Neural Networkの化学分野への応用Post navigation

代襲相続・再転相続・数次相続の法律と実務/安達敏男/吉川樹士【1000円以上送料無料】
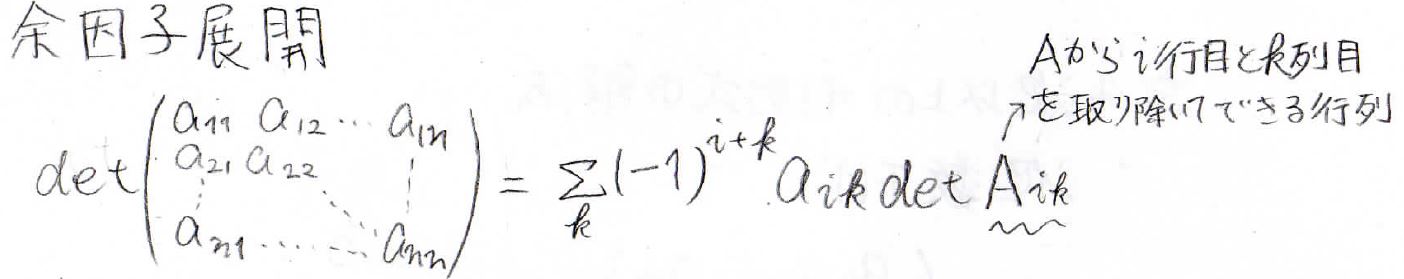
【大学の数学】4次以上の大きな行列式の解き方(次数下げ、余因子展開)を丁寧に解説!

f:id:daynap1204:20170425120416p:plain
![数次相続・代襲相続をめぐる実務[本/雑誌] -相続人・相続分の確定- / 中込一洋/著](https://thumbnail.image.rakuten.co.jp/@0_mall/neowing-r/cabinet/item_img_2030/neobk-2805043.jpg?_ex=300x300)
数次相続・代襲相続をめぐる実務[本/雑誌] -相続人・相続分の確定- / 中込一洋/著
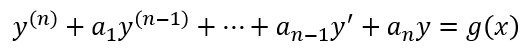
大学初等数学 解法まとめ常微分方程式 ⑩特性方程式を用いる方法(非斉次・定数係数線形微分方程式)コメント
![活躍在?史舞台的藥與毒:有助病人復健的肉毒桿菌、可殺人於無形的香水……無數次改寫人類命運的善惡化學!【電子書籍】[ 齋藤勝裕 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/3089/2000013763089.jpg?_ex=300x300)
活躍在?史舞台的藥與毒:有助病人復健的肉毒桿菌、可殺人於無形的香水……無數次改寫人類命運的善惡化學!【電子書籍】[ 齋藤勝裕 ]
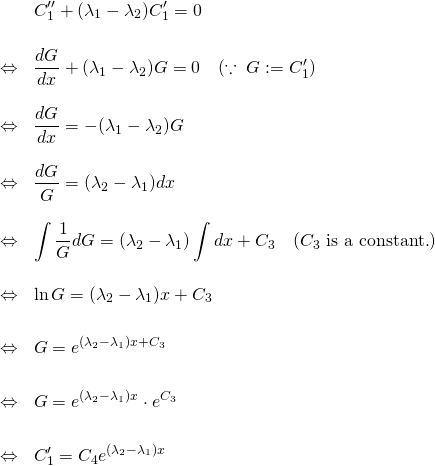
\begin{eqnarray*} && C_1'' + (\lambda_1 - \lambda_2) C_1' = 0 \\ &&\\ &\Leftrightarrow& \frac{dG}{dx} + (\lambda_1 - \lambda_2) G = 0 \quad(\because \; G:=C_1') \\ &&\\ &\Leftrightarrow& \frac{dG}{dx} = - (\lambda_1 - \lambda_2) G \\ &&\\ &\Leftrightarrow& \frac{dG}{G} = (\lambda_2 - \lambda_1) dx \\ &&\\ &\Leftrightarrow& \int \frac{1}{G} dG = (\lambda_2 - \lambda_1) \int dx + C_3 \quad (C_3 \text{ is a constant.}) \\ &&\\ &\Leftrightarrow& \ln G = (\lambda_2 - \lambda_1) x + C_3 \\ &&\\ &\Leftrightarrow& G = e^{(\lambda_2 - \lambda_1) x + C_3} \\ &&\\ &\Leftrightarrow& G = e^{(\lambda_2 - \lambda_1) x }\cdot e^{C_3} \\ &&\\ &\Leftrightarrow& C_1' = C_4 e^{(\lambda_2 - \lambda_1) x } \end{eqnarray*}

Yahoo!知恵袋回帰分析を行う際、線形で近似していいかどうかを判断する方法は存在しますか?

Yahoo!知恵袋この画像にあるような非斉次二階線形常微分方程式の解き方を教えてください定石的に解けるものなのでしょうか?
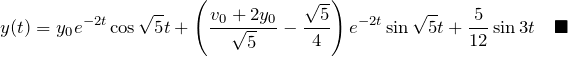
\begin{eqnarray*} y(t)=y_0 e^{-2t}\cos\sqrt{5}t +\left(\frac{v_0 + 2y_0}{\sqrt{5}}-\frac{\sqrt{5}}{4}\right)e^{-2t}\sin\sqrt{5}t +\frac{5}{12}\sin 3t\quad\blacksquare \end{eqnarray*}
![當星星殞落 ?若神真的存在,我必然因為無數次祈求星星的殞落而被降罪。【電子書籍】[ 莫斯?托 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/2775/2000009702775.jpg?_ex=300x300)
當星星殞落 ?若神真的存在,我必然因為無數次祈求星星的殞落而被降罪。【電子書籍】[ 莫斯?托 ]

数次相続・代襲相続をめぐる実務-相続人・相続分の確定- / 中込一洋 【本】


![数次相続・代襲相続をめぐる実務ー相続人・相続分の確定ー【電子書籍】[ 中込一洋 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/9339/2000012649339.jpg?_ex=300x300)

![数次相続・代襲相続をめぐる実務ー相続人・相続分の確定ー [ 中込 一洋 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/0921/9784788290921_1_2.jpg?_ex=300x300)

![代襲相続・再転相続・数次相続の法律と実務[本/雑誌] / 安達敏男/著 吉川樹士/著](https://thumbnail.image.rakuten.co.jp/@0_mall/neowing-r/cabinet/item_img_2030/neobk-2799082.jpg?_ex=300x300)












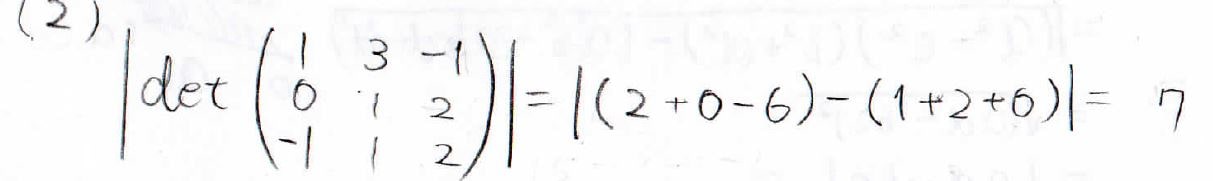
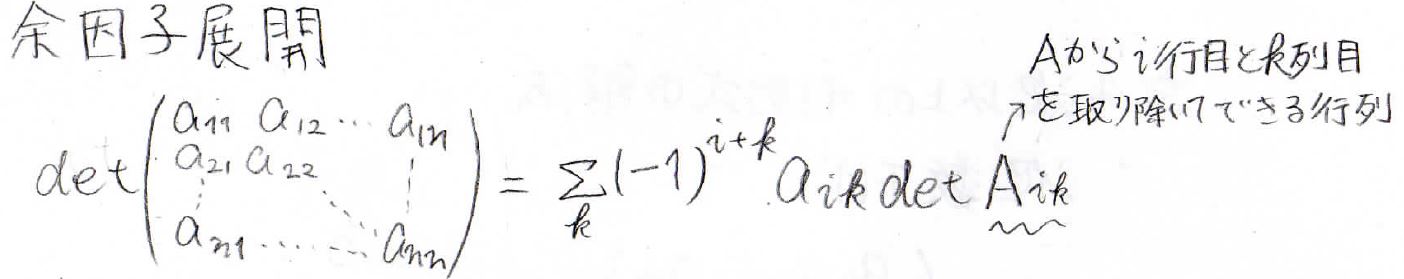

![数次相続・代襲相続をめぐる実務[本/雑誌] -相続人・相続分の確定- / 中込一洋/著](https://thumbnail.image.rakuten.co.jp/@0_mall/neowing-r/cabinet/item_img_2030/neobk-2805043.jpg?_ex=300x300)




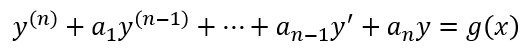
![活躍在?史舞台的藥與毒:有助病人復健的肉毒桿菌、可殺人於無形的香水……無數次改寫人類命運的善惡化學!【電子書籍】[ 齋藤勝裕 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/3089/2000013763089.jpg?_ex=300x300)



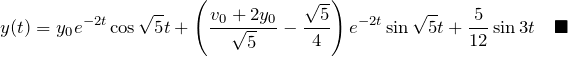
![當星星殞落 ?若神真的存在,我必然因為無數次祈求星星的殞落而被降罪。【電子書籍】[ 莫斯?托 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/2775/2000009702775.jpg?_ex=300x300)




