![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [文庫]【宅配便出荷】](https://thumbnail.image.rakuten.co.jp/@0_mall/mottainaihonpo-omatome/cabinet/07549409/bkojbc7jy1shmnxe.jpg?_ex=300x300)
【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [文庫]【宅配便出荷】

予測に用いる数学見る/開く - 鹿児島大学研究テーマ: 状況・状態把握技術『論理と形式化』資料 No.0 言語 1 一階述語論理の言語研究テーマ: 状況・状態把握技術基本編 理論 - 公益社団法人 沖縄県理学療法士協会Document基本編 理論 - 公益社団法人 沖縄県理学療法士協会カメラキャリブレーション研究テーマ: 状況・状態把握技術研究テーマ: 状況・状態把握技術スライド 1命題論理PDF 版 - 電気電子工学科「南九州から南西諸島における総合的防災研究の 推進と地域防災体制の数理論理学 第1回スライド 1研究テーマ: 状況・状態把握技術expydoc.comYour ExpyDoc

Yahoo!知恵袋一階述語論理式において
∀x( P(x)∧Q(x) )≡∀xP(x)∧∀yQ(y)
が成り立つ意味がわかりません。
xが女の人、yが男の人として、P(x)=xは人間である。
![恋と禁忌の述語論理[本/雑誌] (文庫い 144- 3) / 井上真偽/〔著〕](https://thumbnail.image.rakuten.co.jp/@0_mall/neowing-r/cabinet/item_img_1266/neobk-2310251.jpg?_ex=300x300)
恋と禁忌の述語論理[本/雑誌] (文庫い 144- 3) / 井上真偽/〔著〕
![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [新書]【宅配便出荷】](https://thumbnail.image.rakuten.co.jp/@0_mall/mottainaihonpo-omatome/cabinet/06889058/bkmslpcv2laadvhb.jpg?_ex=300x300)
【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [新書]【宅配便出荷】

後輩指導|序論|論理的に文章を書くためのコツは、『重なり合い』と『主語と述語の明確化』ですよ、の話
![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [新書]【メール便送料無料】【最短翌日配達対応】](https://thumbnail.image.rakuten.co.jp/@0_mall/comicset/cabinet/06891327/bkmslpcv2laadvhb.jpg?_ex=300x300)
【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [新書]【メール便送料無料】【最短翌日配達対応】
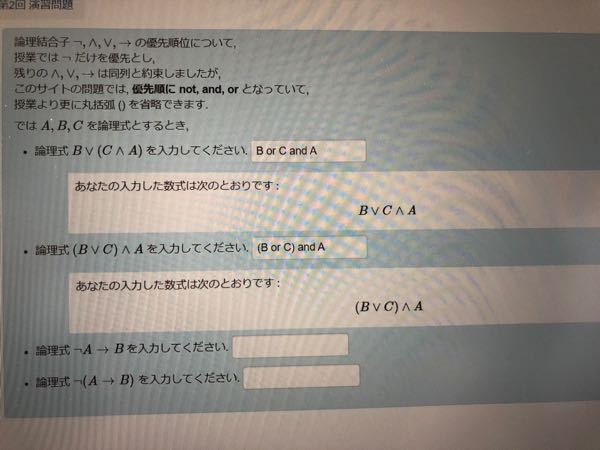
Yahoo!知恵袋述語論理式について
述語論理式を冠頭連言標準形への変換の仕方について教えてください。
一応一通りの変換方法は存じているつもりです。
しかし、以下の問題がわかりません。

k-bijutukanのブログ 『述語的世界と制度』「補章 場所から述語的世界へ」一
![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [文庫]【メール便送料無料】【最短翌日配達対応】](https://thumbnail.image.rakuten.co.jp/@0_mall/comicset/cabinet/07553073/bkojbc7jy1shmnxe.jpg?_ex=300x300)
【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [文庫]【メール便送料無料】【最短翌日配達対応】

【中古】 情報の論理数学入門 ブール代数から述語論理まで/小倉久和,高浜徹行【共著】

恋と禁忌の述語論理(プレディケット)/井上真偽【3000円以上送料無料】
![第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の述語論理への拡張 個体に注目し,「個体について何が述べられてい るか」という観点から命題の内部構造を記述 対象領域: 議論の対象となる個体の集合 ・∀x[J(x)→M(x)] ・J(a) a:](https://present5.com/presentation/33513a9e07c62a00b179d3f94f871879/image-23.jpg)
第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の述語論理への拡張 個体に注目し,「個体について何が述べられてい るか」という観点から命題の内部構造を記述 対象領域: 議論の対象となる個体の集合 ・∀x[J(x)→M(x)] ・J(a) a:

恋と禁忌の述語論理(プレディケット)/井上真偽【1000円以上送料無料】

kazz の数学旅行記 (等号) 述語論理, 形式的体系のモデル, ゲーデル数についての解説.



![恋と禁忌の述語論理 (講談社文庫) [ 井上 真偽 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/9950/9784065139950_1_11.jpg?_ex=300x300)



![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [文庫]【宅配便出荷】](https://thumbnail.image.rakuten.co.jp/@0_mall/mottainaihonpo-omatome/cabinet/07549409/bkojbc7jy1shmnxe.jpg?_ex=300x300)
![恋と禁忌の述語論理[本/雑誌] (文庫い 144- 3) / 井上真偽/〔著〕](https://thumbnail.image.rakuten.co.jp/@0_mall/neowing-r/cabinet/item_img_1266/neobk-2310251.jpg?_ex=300x300)





![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [新書]【宅配便出荷】](https://thumbnail.image.rakuten.co.jp/@0_mall/mottainaihonpo-omatome/cabinet/06889058/bkmslpcv2laadvhb.jpg?_ex=300x300)



![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [新書]【メール便送料無料】【最短翌日配達対応】](https://thumbnail.image.rakuten.co.jp/@0_mall/comicset/cabinet/06891327/bkmslpcv2laadvhb.jpg?_ex=300x300)





![【中古】 恋と禁忌の述語論理 / 井上 真偽 / 講談社 [文庫]【メール便送料無料】【最短翌日配達対応】](https://thumbnail.image.rakuten.co.jp/@0_mall/comicset/cabinet/07553073/bkojbc7jy1shmnxe.jpg?_ex=300x300)






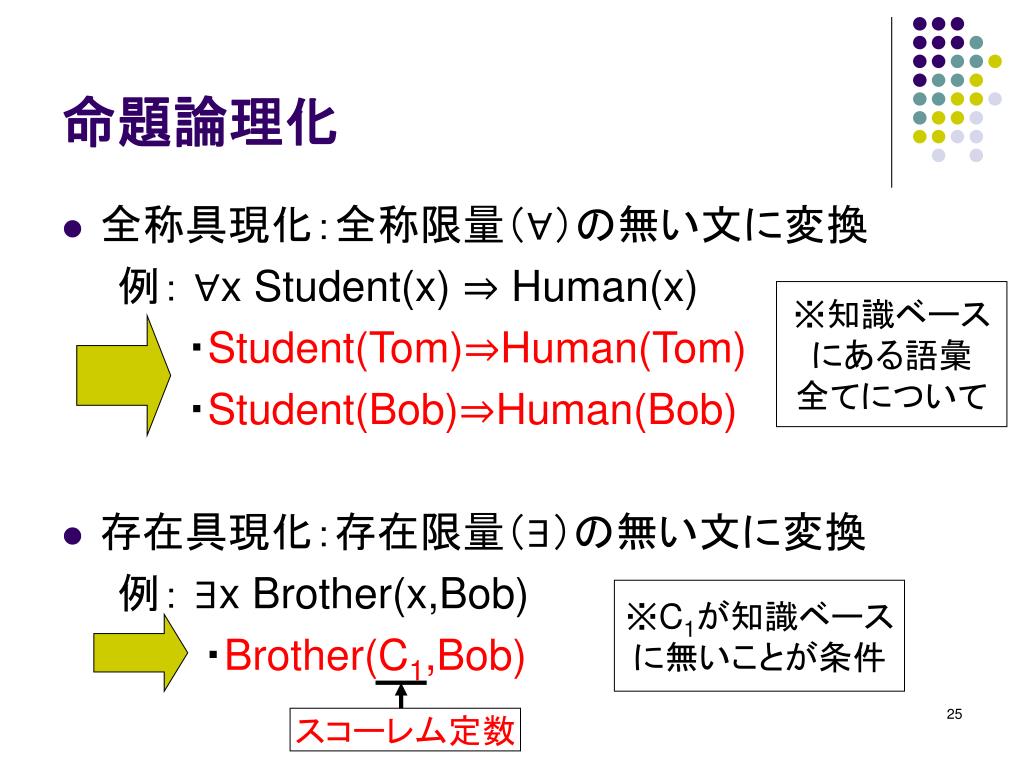



![第9回 一階述語論理 mutty@ics. kagoshima-u. ac. jp 命題論理の述語論理への拡張 個体に注目し,「個体について何が述べられてい るか」という観点から命題の内部構造を記述 対象領域: 議論の対象となる個体の集合 ・∀x[J(x)→M(x)] ・J(a) a:](https://present5.com/presentation/33513a9e07c62a00b179d3f94f871879/image-23.jpg)


