ワッフル ケーキ 10個 | お菓子 洋菓子 詰め合わせ ギフト 個包装 内祝い バレンタイン チョコ以外 ワッフルケーキ スイーツ 冷凍 お取り寄せスイーツ 女性 彼女 妻 誕生日プレゼント…view page
hirakawamakotoStan Advent Boot Camp 3日目; 平均値を推定してみよう本題:平均値について推測してみようPost navigation
view page
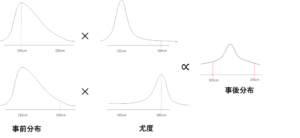
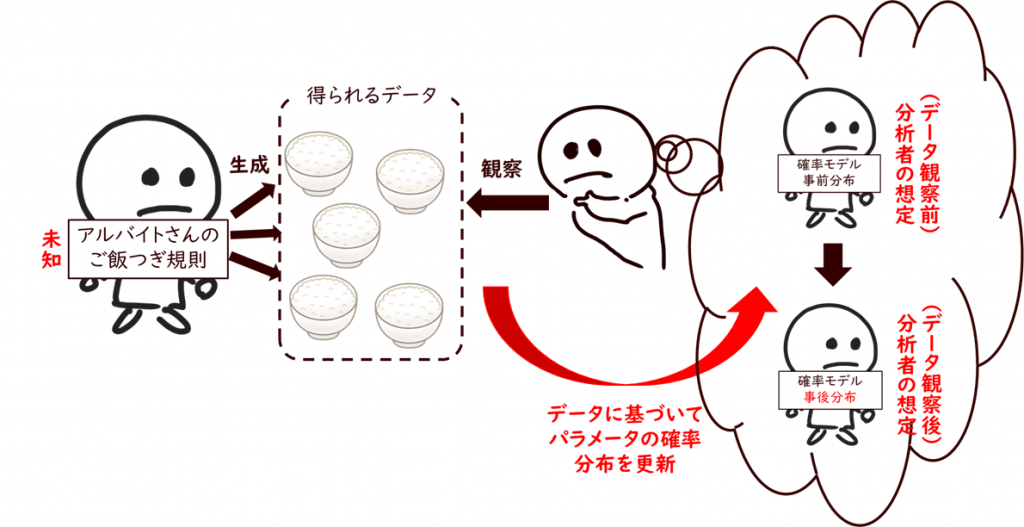
MENUBASIC STUDYPROGRAMMINGAI REPORTABOUT USAVILENベイズの定理の導出と考え方をわかりやすく解説
view page
Doing Bayesian Data Analysis Chapter 11. Null Hypothesis Significance TestingDoing Bayesian Data Analysis Chapter 11. Null Hypothesis Significance Testing
view page
バレンタイン ギフト プレゼント 2026 百貨店で人気 お菓子 【パティスリーキハチ 公式】 人気 おしゃれ 高級 ギフト ランキング 洋菓子 内祝い お返し キハチ 焼き菓子 焼菓子…view page
トレンドニュースサイト STRAIGHT PRESS【 ストレートプレス 】【グランサガ】大型アップデート実施!新プレイアブルキャラクター「ミココロ(Cv.雨宮天)」参戦!
view page
Jeffreysの事前確率とBDeuの一致性に関する比較Jeffreysの事前確率とBDeuの一致性に関する比較
view page
「勝間和代が徹底的にマニアックな話をするYouTube」が新しいYouTube動画「失敗しても落ち込まないコツ。それは事前に失敗確率を実績から予測しておくことです」を投稿しました!
view page
【期間限定★20,000円OFFクーポン+P5倍!】 電動自転車 a01 折りたたみ 電動アシスト自転車 erway 自転車 電気自転車 パワフル 5段階アシスト搭載 20インチ 7段変速…view page
JAGS:事前確率分布の差(θ[1] - θ[2]) りんだろぐ rindalog
view page
二項分布で最尤推定/MAP推定/ベイズ推定をするこれはなに問題設定最尤推定/MAP推定/ベイズ推定の違い
view page
【無料★特典付】 【特別価格】水受けセット ユニソン スプレスタンド60ソリッド 蛇口1個セット+ステンレスパン 蛇口付き立水栓 水栓柱&ガーデンパン 組合せセット 4カラー 1口水栓柱…view page
【LINE追加で最大2000円OFF】 ガスコンロ リンナイ ガステーブル パールクリスタル ホワイト 白 59cm 両面焼きグリル プロパン 都市ガス 据置型ガスコンロ 2口…view page
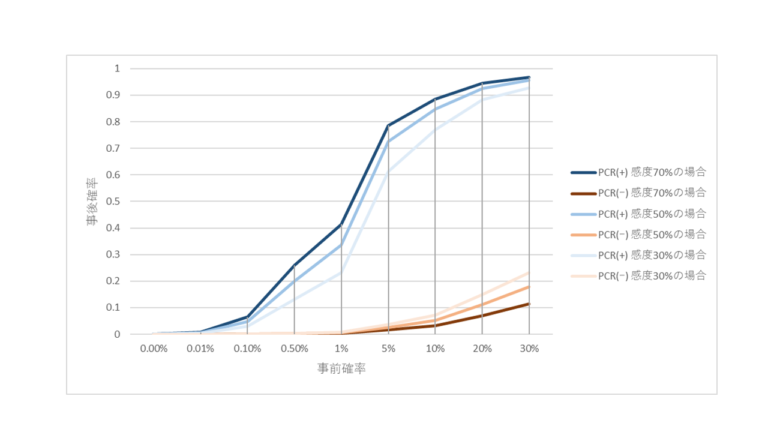
「事前確率が低いと偽陽性だらけになるから無闇に検査してはいけない」は誤り
view page
【期間限定★35,000円OFFクーポン+P5倍!】 サスペンション搭載 型式認定済 電動自転車 免許不要 130km走行可能 a02 折りたたみ 電動アシスト自転車 20インチ 自転車…view page
ITエンジニアのための機械学習理論入門8.1ベイズ推定ITエンジニアのための機械学習理論入門8.1ベイズ推定
view page
【楽天1位!5年保証】シーリングライト 照明器具 LED 調光調色 おしゃれ 電気 北欧 照明 6畳 8畳 10畳 12畳 14畳 リモコン付き LED対応 インテリア 間接照明 天井照明…view page
【DBDA勉強会2013】Doing Bayesian Data Analysis Chapter 8: Inferring Two Binomial Proportions via Gibbs Sampling【DBDA勉強会2013】Doing Bayesian Data Analysis Chapter 8: Inferring Two Binomial Proportions via Gibbs Sampling
view page
15分でわかる(範囲の)ベイズ統計学15分でわかる(範囲の)ベイズ統計学
view page
【ヨドバシ福袋2024】11月27日抽選エントリー開始!種類や中身、当選確率アップの方法は?
view page
期間値引クーポンあり ドレッサー おしゃれ 女優ミラー《自社製品》可愛い デスク 欧風 鏡台 お姫系 ベロア調 テーブル 幅80cm 幅60cm 幅100cm チェスト スツール LEDミラー…view page
楽天カード、最大5万ポイント当たる年末買い物応援キャンペーン。条件に応じて当選確率アップも
view page
【納期お問合せ下さい】 UNISON ガーデンシンク バル 立水栓 バルスタンド トールポット 上下蛇口 セット BARU 水栓柱 ユニソン 補助蛇口 ホース用 2口 ガーデンポット サテン…view page
応接セット 4点セット 4人 応接 ソファ 椅子 応接テーブル ソファセット 応接室 おしゃれ モダン 会議セット 商談 オフィス コンパクト シャルマン SA681-2-T13Sview page
脳はベイジアンなのに、なぜ正しく確率の計算ができないのか?脳がベイジアンだと思われる件それにしては私たちの確率計算があまりにもしょぼ過ぎる件脳はベイジアンだが確率を計算していない件メトロポリス・ハスティング法(MCMCの1つ)人生は"Good-enough"な解が見つかれば意外となんとかなる件
view page
日本音響学会春季発表会2017 「コンテキスト事後確率のSequence-to-Sequence学習を用いた音声変換」日本音響学会春季発表会2017 「コンテキスト事後確率のSequence-to-Sequence学習を用いた音声変換」
view page
\begin{eqnarray*} P(B_2|A)&=&\displaystyle \frac{\displaystyle \frac{1}{3} \times \displaystyle \frac{1}{2}}{\displaystyle \frac{1}{3}\times \displaystyle \frac{1}{5}+\displaystyle \frac{1}{3}\times \displaystyle \frac{1}{2}+\displaystyle \frac{1}{3}\times \displaystyle \frac{2}{3}}\\ &=&0.366 \end{eqnarray*}
view page
ペーパーポット ティッシュケース おしゃれ トイレットペーパー 対応 ティッシュホルダー ティッシュカバー かわいい 丸型 ボックスティッシュ対応 Aicollection アイコレクション…view page
【20%OFFクーポン!LINE追加で今すぐ使える☆】 iphone16 ケース iphone15 ケース スマホケース カード iphone14 ケース iphone13 ケース…view page
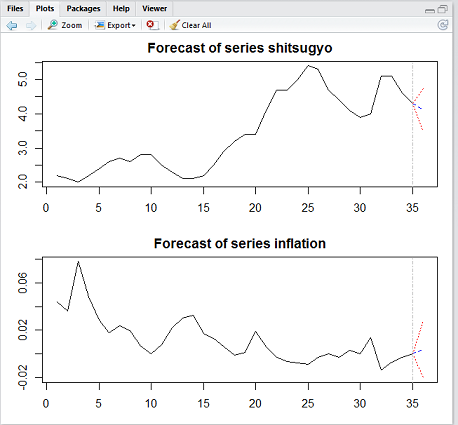
第5章 時系列データのモデリング, 補助情報を考慮したモデリング第5章 時系列データのモデリング, 補助情報を考慮したモデリング
view page
ACTUS カタログギフト<SHINRIN(森林)> 内祝い 結婚祝い 結婚内祝い 出産祝い 引き出物 カタログ ギフト グルメ おしゃれ 結婚 内祝 引出物 引越し祝い 引っ越し 新築祝い…view page
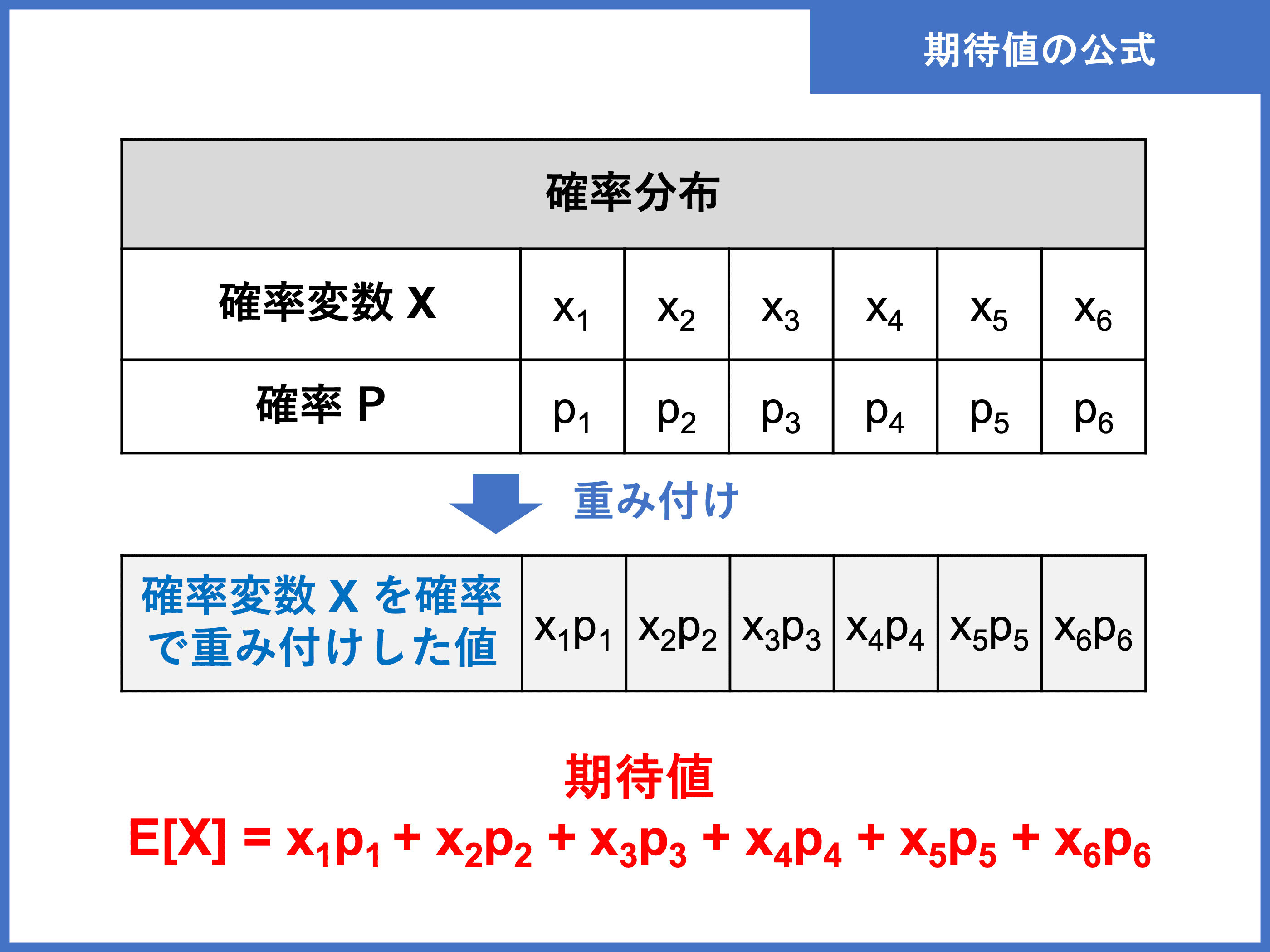
条件付き確率とは?公式を使ってサイコロ・玉の問題を解いてみよう![くじ引きを用いた例題付き]
view page




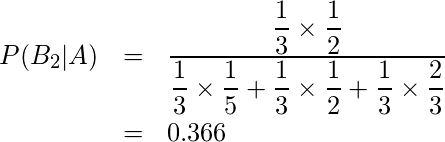








![JAGS:事前確率分布の差(θ[1] - θ[2]) りんだろぐ rindalog](https://4.bp.blogspot.com/-Lv2M62MPXKo/V4bl3Gs5iCI/AAAAAAAAS1k/8DM8zpaRCegQjR54wlThSigRHNP1F3ExACLcB/s1600/Fig8.7_post.png)







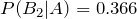

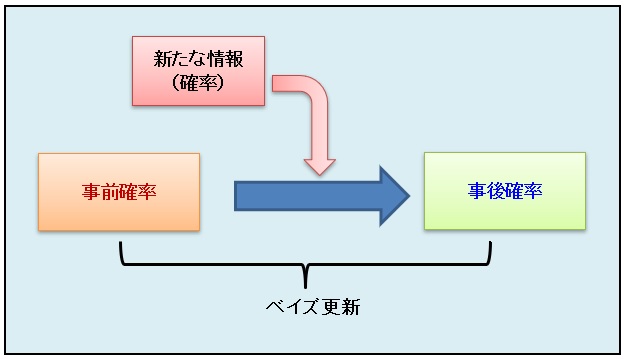






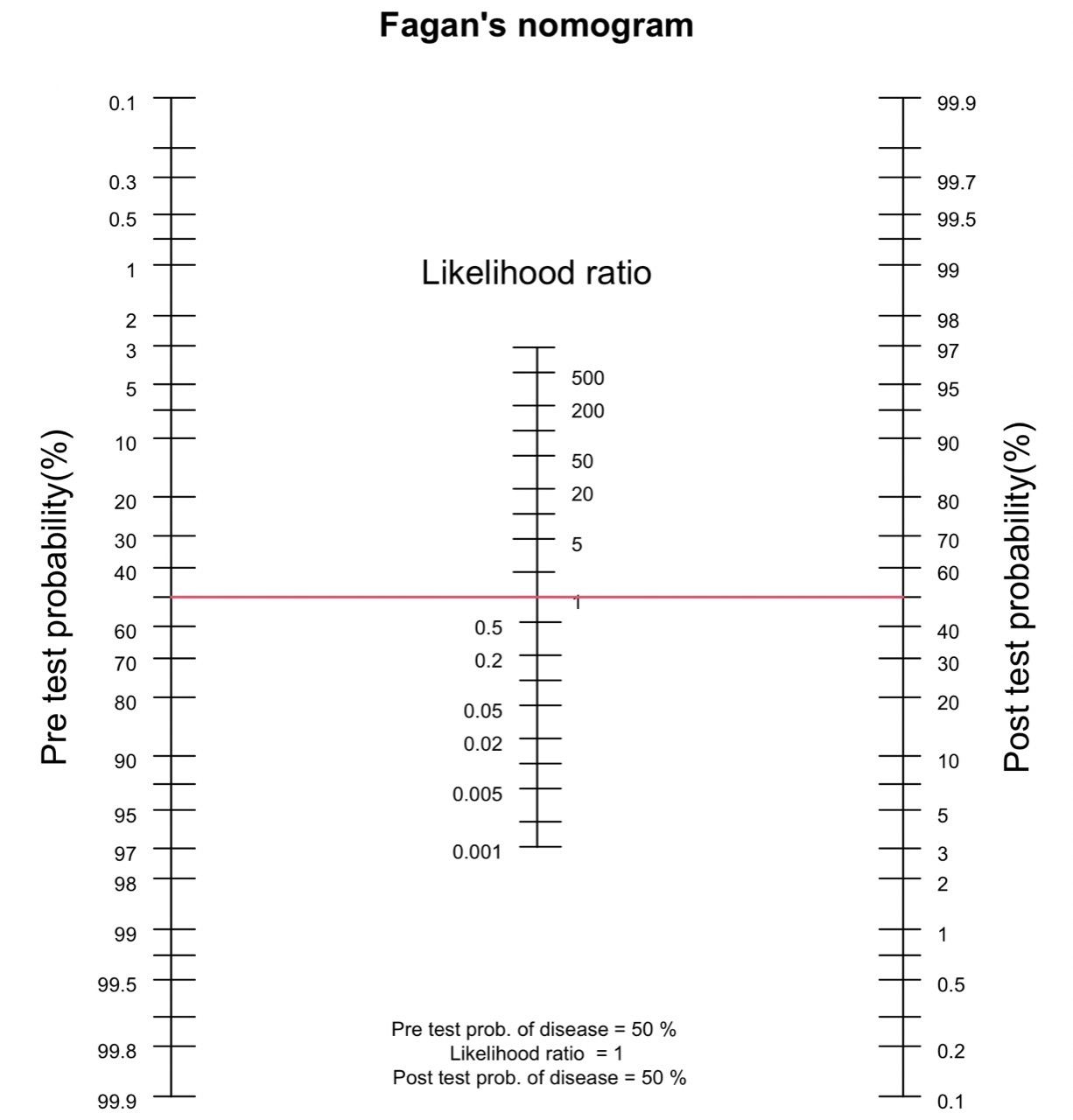















![条件付き確率とは?公式を使ってサイコロ・玉の問題を解いてみよう![くじ引きを用いた例題付き]](https://juken-mikata.sakura.ne.jp/wp-content/uploads/2018/06/39c4f2b2ca5d4d36ddc3011e30c2cd8c.jpg)