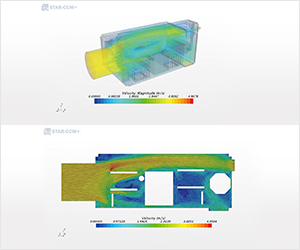
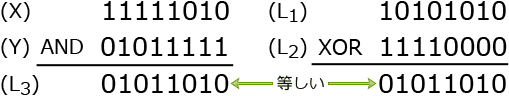2014年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 / 第5回 微分方程式とは,変数分離形 (2014. 10. 23) 2014年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 / 第5回 微分方程式とは,変数分離形 (2014. 10. 23)

エラスリス アコンカグア アルト カルメネール 2019年 エデュアルド チャドウィック チリ アコンカグア ヴァレーErrazuriz ACONCAGUA ALTO Carmenere 2019…

【全品半額coupon事前配布中】ピールオフ ベースジェル “ペロリン” ベースに塗ってジェルネイルをするだけで剥がせる! オフ | ジェルネイル ベース はがせる クリアジェル ネイル…

偏微分方程数值解法(第3版) 下载 mobi epub pdf 电子书 2023
![OPI オーピーアイ ベースコート 15ml NTT10 国内正規品 O・P・I ベース・トップコート [0015/NTT10] メール便無料[A][TG100] ナチュラルネイル ベースコート マニキュア 保護](https://thumbnail.image.rakuten.co.jp/@0_mall/cosmenana/cabinet/10585/1058502015.jpg?_ex=300x300)
OPI オーピーアイ ベースコート 15ml NTT10 国内正規品 O・P・I ベース・トップコート [0015/NTT10] メール便無料[A][TG100] ナチュラルネイル ベースコート…

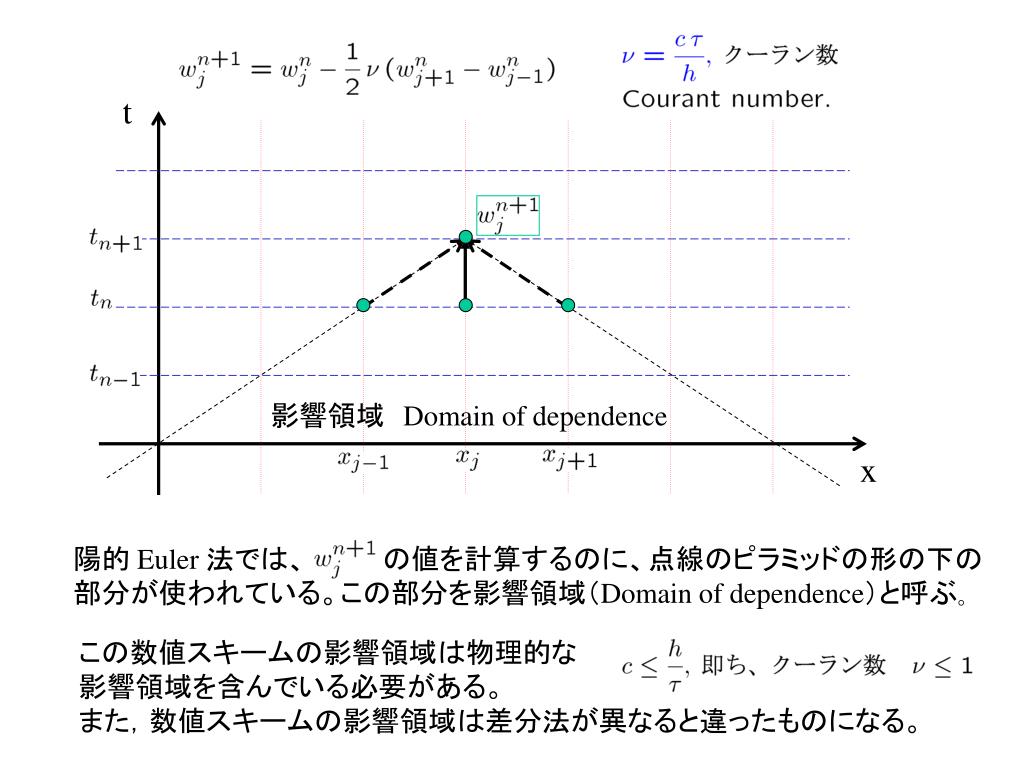
微分方程式の数値解法 (具体例その1: オイラー (Euler) の方法 ) 近似誤差を Order( h 2 ) とすると ( h 2 以上の高次の h の関係式を無視すると ) ,

№ 826: 偏微分方程式論に出て来る定数ですが、N=10 の場合、発散ですが、ゼロ除算算法で 有限値が出て来るのですが、 この有限値は意味が有るでしょうか。 問題です。 Kiryu, Sheet Music, Math Equations, Music Sheets

\楽天ランキング1位/【メール便OK】胡粉ネイル ベース&トップコート 爪に優しく妊婦さんや子供も使える。ネイルアートに。速乾無添加 京の胡粉ネイル 10ml

【公式】ohora Gel Lamp:OHOL-02 ohora gelnails nail オホーラ ネイル ジェルネイル ネイルシール セルフネイル ネイルステッカー おうちネイル…

【全品半額coupon事前配布中】超高発色 マグネットネイル フルーツの果汁のような透明感あふれる 「FruitMagnet」 カラージェル ジェルネイル クリアカラー フルーツマグネット…

物理数学コース 偏微分方程式Partial Differential Equation

偏微分方程式の積分がわかりません。 写真の通りに問題を解いた後、参考書には答えを積分すると u =

微分方程式の数値解法 (具体例その1: オイラー (Euler) の方法 ) 近似誤差を Order( h 2 ) とすると ( h 2 以上の高次の h の関係式を無視すると ) ,

KOKOIST(ココイスト) ブリーディングインク BI-20 スモーキーマッシュルーム 5mL【水彩アート 絵の具 大理石 滲みアート ニュアンスネイル べっ甲ネイル 茶 ブラウン 簡単…

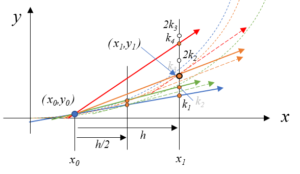
常微分方程初值问题: 一种改进的 Runge-Kutta-Fehlberg 方法

2014年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 / 第7回 2階線形微分方程式(1) (2014. 11. 6)2014年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 / 第7回 2階線形微分方程式(1) (2014. 11. 6)

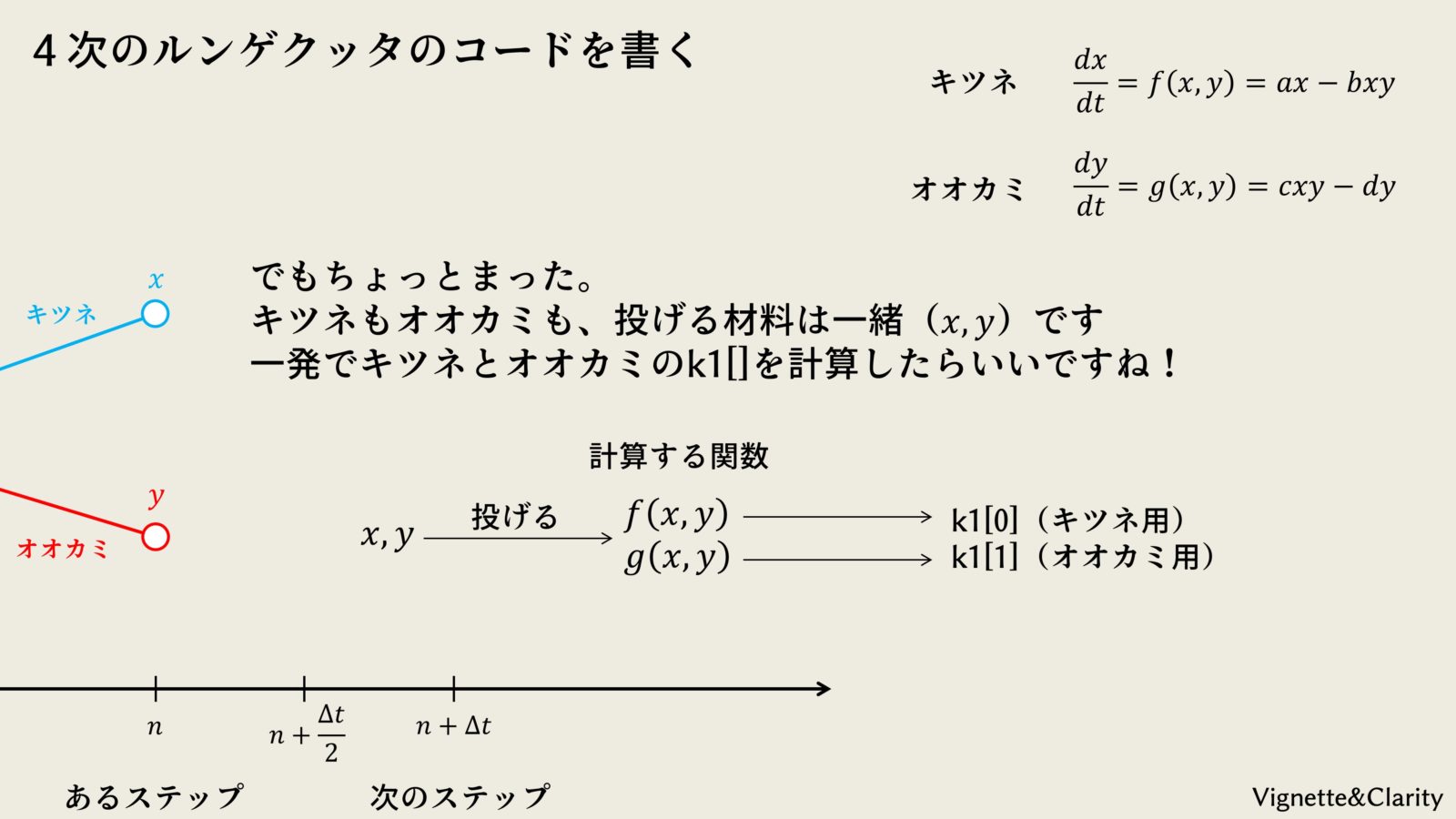
物理数学コース 常微分方程式Ordinary Differential Equations

【送料無料(ゆうパケット)】BRO. FOR MEN Nail Coat クリア【メンズ 男性用 ネイルコート 爪 保護 ネイルケア】

NAIL DE DANCE ネイルデダンス パウダー 001 コサックホワイト 20g

f:id:equal_l2:20150524011818p:plain

オールオルン ネイル メイクアップ allolun make up キッズコスメ キッズ用コスメ スター ネイルカラー STAR NAIL COLOR 剥がせる おしゃれ コスメ メイク 化粧品…

ディズニープリンセス キッズ ネイルチップ 12ピース 18774 ネイル ネイルグッズ つけ爪 つけづめ ネイルアート 接着剤付き おしゃれ カラフル 子供 こども かわいい 女の子…

2014年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 / 第5回 微分方程式とは,変数分離形 (2014. 10. 23)2014年度秋学期 応用数学(解析) 第2部・基本的な微分方程式 / 第5回 微分方程式とは,変数分離形 (2014. 10. 23)

検定用品 イクステンション ネイルデダンス Nail de Dance パウダー 004 ルンバナチュラル 20g アクリル ねいるでだんす…






![[学习心得]---浅谈一阶非齐次线性常微分方程的特解——积分因子法](https://pic3.zhimg.com/v2-ad739aae7b754f00d8b9d94193baec06_r.jpg)


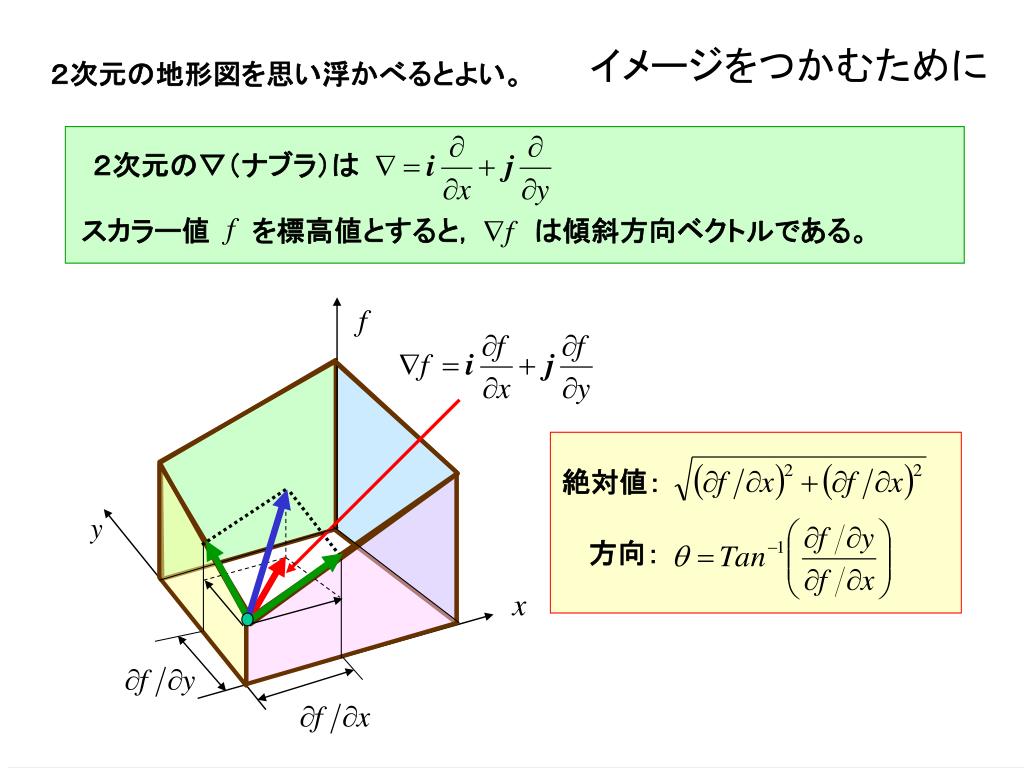
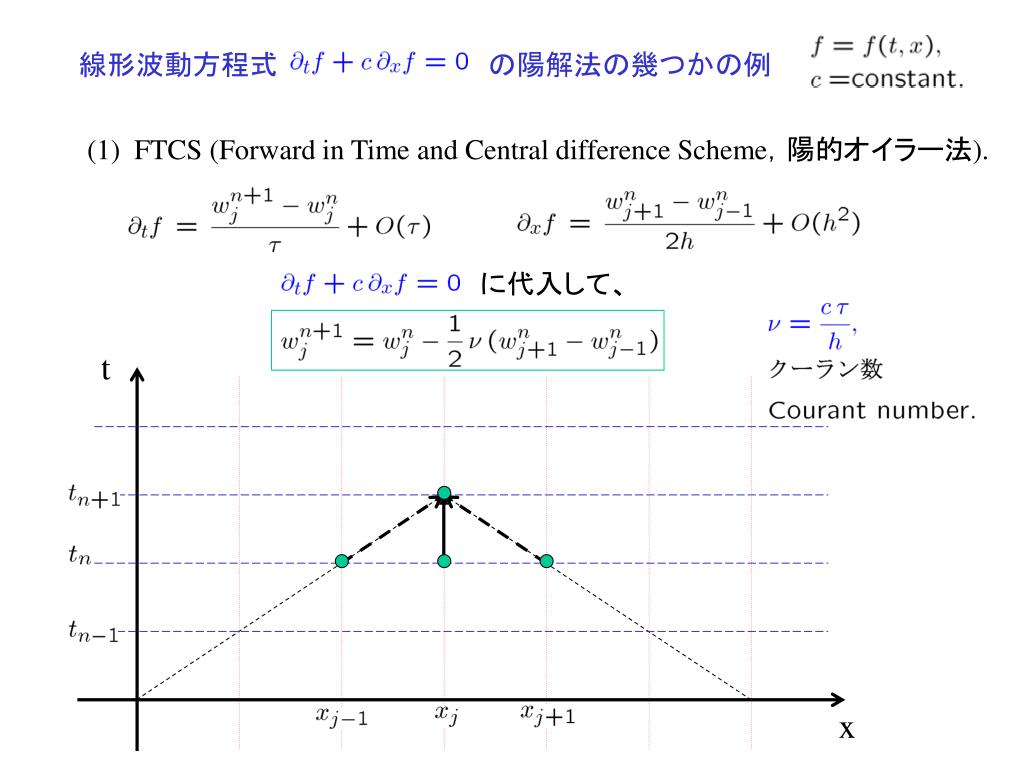
![OPI オーピーアイ ベースコート 15ml NTT10 国内正規品 O・P・I ベース・トップコート [0015/NTT10] メール便無料[A][TG100] ナチュラルネイル ベースコート マニキュア 保護](https://thumbnail.image.rakuten.co.jp/@0_mall/cosmenana/cabinet/10585/1058502015.jpg?_ex=300x300)








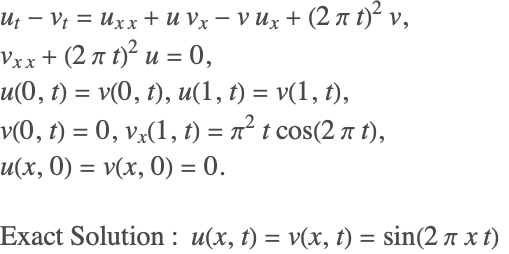

















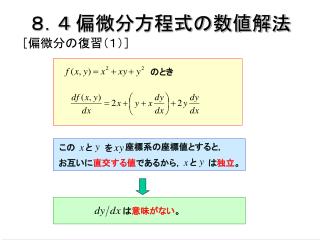

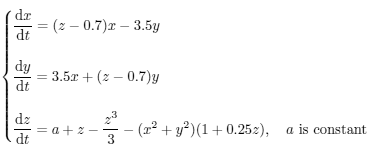







![[学习心得]---浅谈一阶非齐次线性常微分方程的特解——积分因子法](https://pic1.zhimg.com/v2-d1fc318dec7599db57faa0efaa7359da_r.jpg)