Images of 条件収束

広義積分の収束条件 view page

[新品未開封｜未使用品｜SIMフリー] iPhone 16e 128GB 256GB 512GB ホワイト ブラック アイフォン16e 本体 スマホview page

3本の移動平均線収束個所表示インジケーター2 view page

Kernel-KmeansのNumpy実装 view page

緊急事態宣言　14日検討は早急か？解除の条件や収束への課題を考察 view page

【4日20時からポイントUP! お買い物マラソン】新品未開封品【Nランク】SIMフリー iPhone16 256GB Apple A3286 ブラック ホワイト ピンク ウルトラマリン ティール【…view page

電磁界解析ソフトウェア電磁界解析ソフトウェア view page

ζ(4) view page

【数列の極限の大小関係】イメージでわかる、知っててアタリマエの公式 view page

【新登場】iPhone 16e simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン…view page

広義積分の収束条件 view page

はじめてみよう！流体解析（入門編）［Ⅳ］～流体解析の作業工程～ view page

励振源・境界条件・収束判定・解析の実効値【電磁波解析の基礎用語】 view page

iPhone 16 simフリー 端末本体のみ（機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン 【ご注文から30分経過後はキャンセル不可】【自宅受け取り限定 /…view page

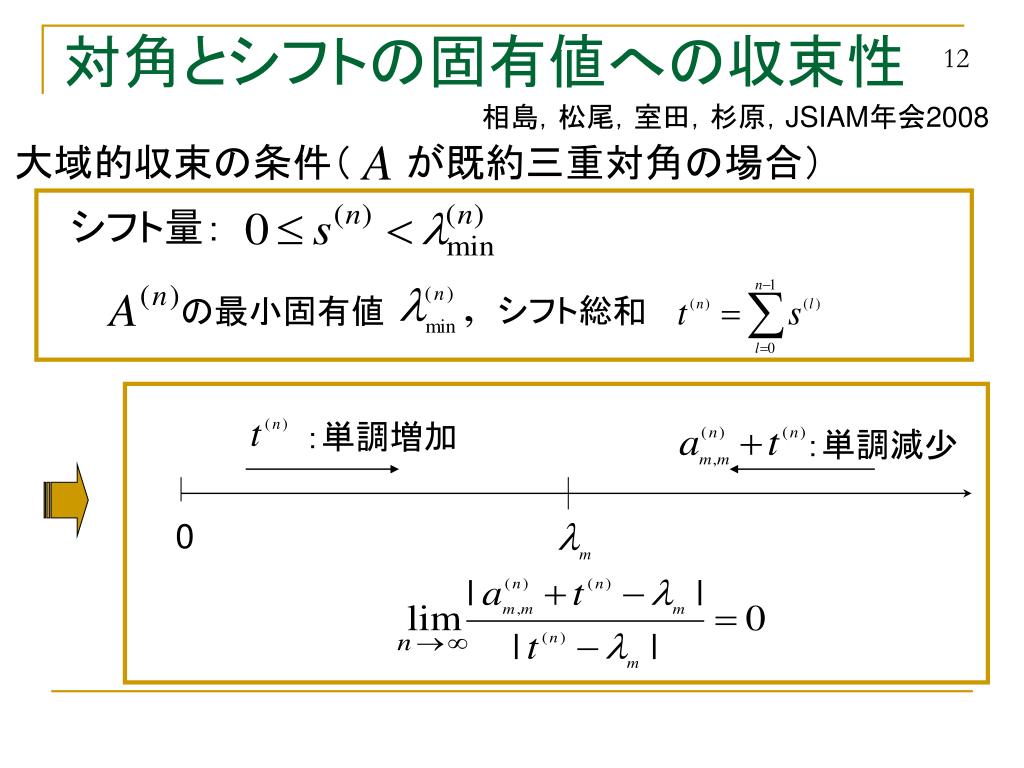
シフト付きコレスキー LR 法における ２つの固有値近似法の収束性について view page

身勝手な主張 view page

Yahoo!知恵袋この整級数の収束半径って何になりますか？ view page

【中古】iPhone 14 128GB 256GB 512GB A2881 スマホ スマートフォン 本体 SIMフリー ミッドナイト (PRODUCT)RED スターライト パープル ブルー…view page

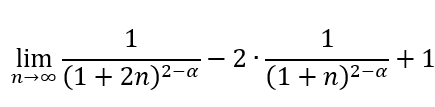
Yahoo!知恵袋電気回路、四端子定数についてです。 以下図5,6,7の二端子対回路において、F行列を解説込みで求めていただけないでしょうか。 与えられた値はR=1.5kΩ、C=1.0µF、f=1.2kHz。 view page

シフト付きコレスキー LR 法における ２つの固有値近似法の収束性について view page

条件収束級数は和の順序交換により任意の値に収束できることの証明 view page

[新品未開封｜SIMフリー] iPhone 16 128GB 256GB 512GB 各色 スマホ 本体view page

条件収束級数は和の順序交換により任意の値に収束できることの証明 view page

反省会について view page

四ツ谷のバレリーナ専門気功整体「Rayまといのば」いくつも広がる世界線を、Goalに沿って意図することで選び、行きたい世界へ転生していきましょう！ view page

【中古】iPhone 13 128GB 256GB 512GB A2631 スマホ スマートフォン 本体 SIMフリー グリーン ピンク ブルー ミッドナイト スターライト…view page

GSM 日本周辺 地上風流線/収束発散 view page

JavaScript is not available. view page

GSM 日本周辺 地上風流線/収束発散 view page

iPhone 16 Pro Max simフリー 端末本体のみ （機種変更はこちら）新品 純正 Apple 認定店 楽天モバイル公式 アイフォン…view page

図形を利用した定積分の計算 view page

6本の移動平均線収束個所表示インジケーター view page

【ディニの定理】各点収束から一様収束が従う定理とその証明 view page

【中古】iPhone SE 3 第3世代 2022 A2782 64GB 128GB スマホ スマートフォン SE3 本体 SIMフリー ミッドナイト レッド スターライト docomo au…view page

関数列の各点収束、一様収束とは、例と違い、求め方 view page

Yahoo!知恵袋英語で論文を書く場合、「式」（数式）はどのような英語で表記するのでしょうか？ 「formula」でしょうか？ view page

junologyのブログ 超関数の収束とδ関数の表式 view page

【4日20時からポイントUP! お買い物マラソン】新品未開封品【Nランク】SIMフリー iPhone16 Pro 128GB Apple A3292 ブラックチタニウム ホワイトチタニウム…view page

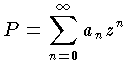
収束半径（読み）しゅうそくはんけい（英語表記）radius of convergence view page

画像 view page

画像 view page

【新品】iPhone 16 Pro 128GB デザートチタニウム MYMX3J/A SIMフリーview page

Yahoo!知恵袋線形代数の部分空間であることを証明する問題です。 次のw ⊂R^3について w = {[x,y,z] | z^2 = x^2 + y^2} を部分空間であると証明したいです。 view page

级数2的n次方*(x的2n次方)的收敛半径？级数2的n次方*(x的2n次方)的收敛半径？ view page

画像 view page

[新品未開封｜未使用品｜SIMフリー] iPhone 15 128GB 256GB 各色 スマホ 本体view page

画像 view page

画像 view page

画像 view page

[国内版SIMフリー・新品未開封/未使用品] iPhone15 128GB 256GB 512GB 各色 スマホ 本体view page

2014年度秋学期　応用数学（解析）　第１部・「無限」の理解　／　第４回　収束とは何か，ε-δ論法 (2014. 10. 16)2014年度秋学期　応用数学（解析）　第１部・「無限」の理解　／　第４回　収束とは何か，ε-δ論法 (2014. 10. 16) view page

lim(n→∞) Σ(k=1,n) n*(5/6)^n view page