Images of 相対論的量子力学

量子力学 : 非相対論的理論 【2】 改訂新版 ＜ランダウ=リフシッツ理論物理学教程＞ view page

相対論的量子力学【電子書籍】[ 川村 嘉春 ]view page

相対論とゲージ場の古典論を噛み砕く—ゲージ場の量子論を学ぶ準備として— view page

▲古典力学、相対性理論、量子論の守備範囲。得意分野と重なる部分がわかると、理解が一気深まる。 view page

相対論的量子場 演算子の基礎的性質 改訂版/吉岡書店/日置善郎 view page

相対論的量子力学 （新物理学シリーズ） [ 西島和彦 ]view page

相対性理論と量子力学の統合理論　超ひも理論に勝てる理論って無いの？ view page

cover image of なっとくする演習･量子力学 view page

相対論対量子論 view page

【中古】 相対論的量子力学 (新物理学シリーズ 13)view page

【図解】相対性理論と量子論 – 超難解な「相対性理論」と「量子論」を“数式なし”で理解する！ view page

第4章　経済・社会の高度化に寄与する光　2　光による粒子の加速 view page

Betelgeus-Himawari-8 view page

相対論的量子力学[本/雑誌] (量子力学選書) (単行本・ムック) / 川村嘉春/著view page

物理学習会「高校生のための相対論」 view page

相対論的ゲームを作る相対論的ゲームを作る view page

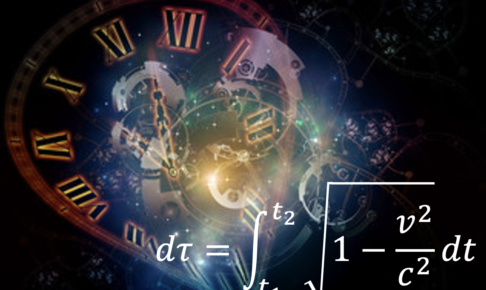
相対論ローレンツ変換の導出「固有時間」と「時間の遅れ」世界間隔が不変であることの証明 view page

相対論的量子力学 量子力学選書 / 川村嘉春 【本】view page

Yahoo!知恵袋一般相対論に関する質問です． よろしくお願いします． view page

東京都内で行者ニンニクを売っているお店 view page

特殊相対論　入門目次この資料について物理学的準備特殊相対論の概要エーテルマイケルソン・モーレの実験放射説絶対基準説特殊相対論ローレンツ変換光行差のアインシュタインによる説明特殊相対論とGPSシステム view page

相対論的量子力学 新物理学シリーズ / 西島和彦 【全集・双書】view page

【全集・双書】 谷島賢二 / 相対論とリーマン幾何学 数学と物理の交差点 送料無料 view page

『一般相対論入門(改訂版)』（著：須藤靖） view page

お探しのページが見つかりません。 view page

相対論的量子力学／川村嘉春【3000円以上送料無料】view page

裳華房テキストシリーズ‐物理学　相対性理論Theory of Relativity view page

相対論 view page

紀伊國屋書店 view page

【中古】 相対論的量子力学 (新物理学シリーズ 13)view page

書籍詳細：もうひとつの一般相対論入門トップページ書籍雑誌デジタルコンテンツ view page

相対論的量子力学 (量子力学2・改訂改題) ＜共立物理学講座 15＞ view page

とね日記 view page

【中古】 相対論的量子力学 (新物理学シリーズ 13)view page

相対論の破れを観測せよ view page

相対論的量子力学　1・2　【2冊】　（ランダウ=リフシッツ理論物理学教程） view page

迷著「なっとくする相対性理論」から学ぼう view page

東京図書 相対論的量子力学 ランダウ＝リフシッツ理論物理学教程 1969 034S6Dview page

f:id:astraysheep:20090921224606j:image view page

ぴかりんの頭の中味 view page

趣味で相対論 view page

相対論的量子力学view page

相対論的ゲームを作る view page

人も獣も樹も花も違いなし、すべて我が友単行本『10分で名著』／今日のエールもらってみた view page

「同じ」を考える -- 「型の理論」入門 view page

【中古】相対論的量子力学 (新物理学シリーズ 13)view page

新装版 相対論的宇宙論 : ブラックホール・宇宙・超宇‪宙‬ view page

花と風景の写真サークル②ぽんちゃんの“RECIPE-DIARY”てっこつ団イタリア！小さなまちと田舎の旅紫仙人の ダイエット塾里山を楽しもう{{ stampcard.name }} view page

NAVERまとめ view page

【未使用】【中古】 相対論的量子力学 (量子力学選書)view page

pgen56a.jpg view page

正規言語と代数と論理の対応：An Introduction to Eilenberg’s Variety Theorem正規言語と代数と論理の対応：An Introduction to Eilenberg’s Variety Theorem view page