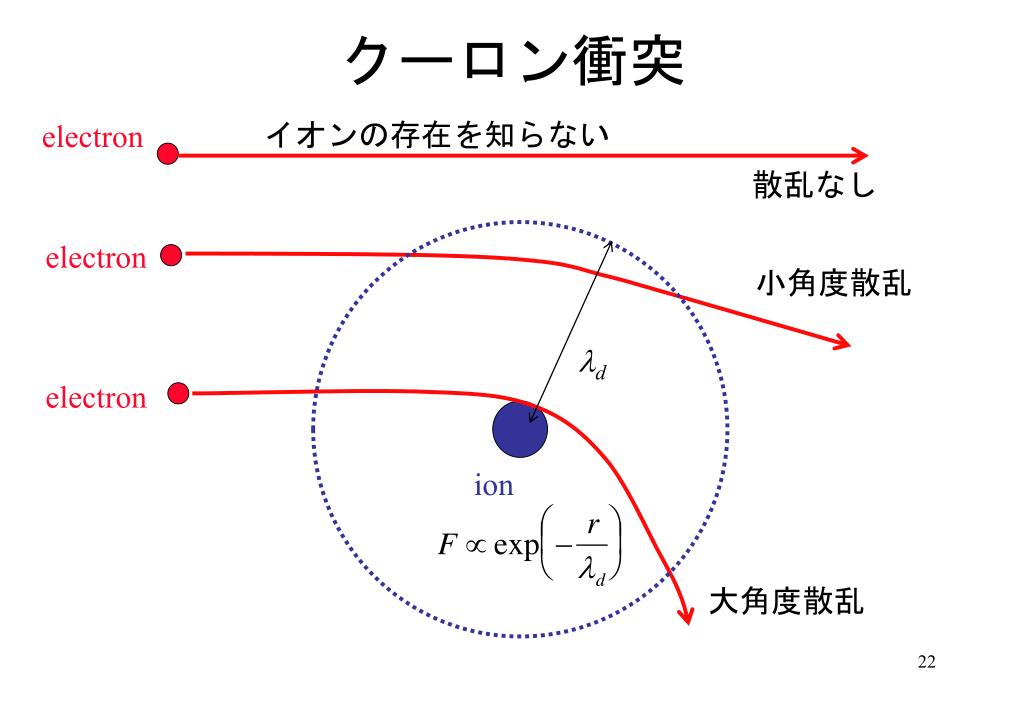
Images of デバイ長

MINISFORUM Unveils AMD Ryzen 9 5900HX CPU Powered EliteMini HX90 Mini PC, An Insanely Fast SFF Solution Starting at $729 US
![コロイドと界面現象<目次> はじめに Ⅰ.コロイドと界面現象 1.コロイドとは 2.疎水・親水コロイド 3.疎水コロイドの分散と凝集 4.親水コロイドの塩析 5.会合コロイドとミセル 6.コロイド溶液の物性 Ⅱ.解説 解説(A) 粒子界面の静電気現象 解説(B) 疎水性2粒子系の相互作用 解説(C) 粒子界面電荷の発生 解説(D) 電解質効果とSchulze-Hardy法則 解説(E) 凝集速度 解説(F) 表面張力と界面活性 解説(G) 界面活性剤の特性 解説(H) 吸着エネルギーと平衡式 解説(J) 高分子吸着と分散・凝集 付録:疎水コロイド相互作用の計算ソフト (ダウンロード) ※本ページは『水浄化フォーラム』より転載しています。<謝辞> 「水」の安全確保と環境保全に係る知識と技術を、「水の浄化」に関わる方への参考となるサイトとして『水浄化フォーラム』を執筆・編集・管理いただいている 環境技術学会 村上理事に心より感謝申し上げます。 はじめに コロイドおよびその現象は、生命を含む自然界において重要な役割を担い、人々の生活・産業においても様々な形で利用されている。水浄化の分野においても、コロイドの制御は主要な要素技術である。 水浄化において、原水中の濁質のうち、粒子径が10μm程度以上のものは単純な沈澱によって除去することが可能である。しかし、粒子径が1μm以下になると、コロイド粒子が懸濁状となり、ほとんど沈降せず、また急速ろ過では捕捉することもできない(図1)。さらに水中に溶解している有害な金属や非金属の原子・分子イオンを難溶性塩や水酸化物(共同沈殿を含む)として析出・沈降して分離除去するとき、1μm以下の微細な結晶性・不定形の粒子を生成するが、10μm程度以上の沈降性粗大粒子にまで成長できない例は少なくない。 わが国の水道における浄水処理において、一般的に、凝集・沈殿・急速砂ろ過を基本としたシステムが採用されている。この技術が微粒子の分離に優れ、安価・大量処理など多くの利点あるため、日本の近代水道が発祥して100年以上経過した現在でもなお主流技術として用いられている。また、種類の異なる様々な懸濁水(溶解性物質を不溶性物質へ変換する工程も含めて)は、建築・建設工事現場や生産・製造工程において発生し、凝集・沈殿分離は基本的な水浄化技術となっている。 以上の凝集工程の設計や維持管理(目次、関連ページ、参照)を適正に実施するためには、コロイドの性質とその分散・凝集の機構を理解することが大切となる。 図1 水浄化における汚濁物質のサイズとその分離・除去法本ページの目的と構成 本ページは、学校・大学の学生や企業での初心者を対象として、「水浄化におけるコロイドの凝集工程についての原理・操作」を理解するための基礎として、「Ⅰ.コロイドと界面現象」、および、「Ⅱ.解説」から構成されている。Ⅰ~Ⅱに記載の内容には、一部、重複したものも含まれている。重複した数式については、サブページを含めて本ページ全体を通して同一の式番号を記載している。文献・Web-Siteの引用 引用・参考にした文献は本ページボトムに示したが、引用した画像や動画はそれぞれのサイトをリンクしてあるので、それらのサイト内容も含めて理解されたい。 Ⅰ.コロイドと界面現象1.コロイドとは 1861年、スコットランドの化学者であるThomas Grahamは、水中でデンプンやタンパク質などの粒子が拡散する速度が遅いこと を発見し、これをコロイド(colloid)と名付けた。コロイド粒子(colloidal particle)とは、直径がおよそ1nm~1μm程度で、単一の 原子・分子サイズと比べて比較的大きな粒子で、媒体中に分散した状態で存在する。 1.1 身近なコロイドの事例 コロイドとは、コロイド粒子(固体や液滴)が他媒体(気体・液体・個体)に分散した系全体のことを指す。身近な例でいえば、牛 乳や泥水などがコロイドである。牛乳のような分散質が液体コロイドの溶液は一般的にエマルション(emulsion)といい、これに対し て、泥水のような分散質が固体コロイドの溶液は一般的にサスペンション(懸濁、suspension)という。 コロイドの分散媒は、液体または固体の場合が多いが、分散媒が気体の場合もあり、そのようなコロイドはエアロゾル(aerosol)と いう。 ゾル(sol)とは流動性を持ったコロイドのことで、これに対して、加熱や冷却などの何らかの原因で、ゾルが流動性を失ったものをゲ ル(gel)という。身近なゲルの例としては、寒天・ゼリー・豆腐などがある。 表Ⅰ-1 身近なコロイドの分類と実例1.2 コロイドの分類 コロイドは、その構造により、① 高分子コロイド(polymer colloid)、② 会合コロイド(association colloid)および ③ 分散コロイ ド(dispersed colloid)に分類される。 高分子コロイドは、分散媒に分散した分子1個の大きさがコロイドサイズの分散系である。コロイド化学の初期には、高分子コロイド の研究がコロイドの主流であった。コロイド研究の先駆者であったThomas Grahamが最初に示したコロイドは、いずれも天然高分 子であった。現在では、高分子化学(polymer chemistry)という別の学問分野ができ上がっているので、高分子をコロイド化学で扱 うことは、少なくなった。 会合コロイドは、多くの分子が集まって、コロイドの大きさを持つようになった分散系を示す。洗剤などの界面活性剤分子は、溶液 中である濃度以上になると、ミセル(micelle)と呼ばれるコロイドサイズの会合体を形成する。 分散コロイドは、溶媒には本来溶解しない不溶性物質の分散系である。溶解するはずのない物質が媒体中で分散しているのだから、 分散コロイドは熱力学的には不安定な系であり、条件によって破壊することができる。表Ⅰ-1で示したコロイドはすべて分散コロイ ドであり、分散コロイドは最も身近に溢れているコロイドである。 表Ⅰ-2 コロイドの種類1.3 コロイドの形状と観察(1) 大きさ コロイド粒子の大きさは直径が1nm~1μmの範囲で、ろ紙を通過するが半透膜を通過しない程度の大きさである。この性質を使 用して分子とコロイド粒子を分けることができる。図Ⅰ-1 コロイド粒子の大きさとその分離(2) 形状 コロイド粒子の形状には、球状、棒状、針状、板状、繊維状、膜状のものなど、コロイド系の物質・分散媒やその生成過程を含め て物理・化学的条件により様々な形状で存在している。図Ⅰ-2 コロイド粒子の形状モデル(3) 観察 コロイド粒子は、光学顕微鏡では小さすぎて観察することができないが、限外顕微鏡や透過型電子顕微鏡(TEM)などを使えば、 コロイド粒子を観察することができる。限外顕微鏡では、特殊な照明装置により微粒子の散乱光(チンダル光)を観察して、微粒子 の動きを見ることができる。また、透過型電子顕微鏡では、可視光の代わりに電子線を照射して、対象を観察することができる。 コロイド粒子は非常に小さいので、これを観察するには特殊な装置が必要となる。 2.疎水・親水のコロイド 2.1 コロイド状態の保持 分散コロイドは、不溶性物質の粒子が媒体中に分散している系のことであって、溶解性物質の溶液とは明確に区別される。溶液は結 晶がその物質の構成単位である原子や分子のレベルまで解離して溶媒に溶けている状態であるのに対して、コロイドは多数の原子・ 分子が集まって1つの粒子(例えば、不溶性の金属酸化物では、1nm粒子でおよそ数百個、1μmでおよそ数×1011個の金属と酸素の 原子から構成される粒子)となり、それらが媒体に分散している状態である。単一分子サイズが大きい高分子コロイドなどの例外も あるが、コロイドは、一般的には「多数の原子・分子から構成される集合体が分散媒に分散している系」である。したがって、コロ イドとして分散状態を保つためには、いくつかの条件が必要となる。 (ⅰ)コロイド粒子がさらに小さな粒子(原子や分子)にまで解離されないこと 例えば、結晶・粉末状の食塩NaClやショ糖C12H22O11は、水中ではNa+・Cl–イオンやショ糖C12H22O11の単分子にまで 解離・溶解しているので、コロイドとはいえない。食塩やショ糖は、水中では結晶・粉末状の状態よりも、解離して水和したイ オン・分子での状態の自由エネルギーが低く、熱力学的に安定であるからである。 (ⅱ)コロイド粒子同士が衝突・凝集し、さらに大きな粗粒子にならないこと 分散コロイドは熱力学的には不安定な系で、コロイド粒子は安定になろうと凝集してより大きな粒子になろうとする作用が働 く。コロイド粒子が凝集して大きな粒子になると、単に浮上するか沈降するかという状態となり、コロイドではなくなってしま う。 分散したコロイド粒子が凝集しないようにするには、主に以下の2つの方法がある。 第一の方法は、コロイド粒子の表面を帯電させることである。例えば、後述する図Ⅰ-5に示すように、コロイド粒子の表面を「正」 に帯電させたとする。このとき、電気的に中性を保とうとして、表面電荷量と同量の負イオンが過剰にコロイド粒子を取り巻いてい る。粒子の表面電荷と反対符号のイオンを対イオン(counter ion)といい、このような状態を電気二重層(electric double layer)が できているという。なお、多数の対イオンは粒子表面の電荷に引かれて統計的に分布しているものの、個々のイオンは自由に液中を 拡散して遠くまで動くことができる。 ところで、ブラウン運動により2つの粒子が接近し、相互の電気二重層が重なるようになると、図Ⅰ-3に示すように、重複した二重 層領域の浸透圧 [= Π(h):h は粒子表面間の距離] の増加による反発力 Po(h)が働き、自由エネルギー [= ∫ Π(h)v(h)dh:h = ∞→h で積分; v(h)は重なり領域の体積] が増大することによって熱力学的に不安定となり、粒子同士の合体を妨げるようになる。 基本的には気体の圧縮に必要な力とそれに要する仕事エネルギーの関係と同じようなものと考えると理解しやすい。ただし、重なり 領域内でのイオン濃度分布が均一でないので、計算は複雑となる。 図Ⅰ-3 電気二重層の重なりによる浸透圧の増加と粒子間反発力の発生 分散コロイドが凝集しないための第二の方法は、図Ⅰ-4に示すように、コロイド粒子の全表面を溶媒分子で覆っておくことであ る。コロイド粒子が互いに接近しても、表面を覆っている溶媒分子が離れなければ、コロイド粒子間の接触を妨げることができ る。図Ⅰ-4 表面が水素結合による水分子層で覆われている親水性粒子同士の接近 2.2 疎水性コロイド コロイド粒子のうち、主に上記の第一の方法のみで水中で分散している場合、これを疎水コロイド(hydrophobic colloid)という。 水に対して不溶であり、本来沈降すべき物質がコロイド粒子のサイズになった上に、何らかの理由(詳しくは、Ⅱ.解説(C)を参 照)で表面が帯電してしまったために、粒子間に反発力が働き、合体・集合できなくて微細な状態のコロイド粒子が分散状態になっ ている。一般的に、疎水コロイドは、その大半が無機物質である。 2.3 親水性コロイド 上記の第二の方法が主たる理由で水中に分散している場合には、これを親水コロイド(hydrophilic colloid)という。コロイド表面に 溶媒である水分子層が付着して離れないのは、水に対して親和性が高いからである。親水コロイドには分子コロイドや会合コロイド が多く、その大半が有機物質である。 表Ⅰ-3 コロイドの分類と特徴3.疎水コロイドの分散と凝集 3.1 DLVO理論による分散・凝集機構 疎水コロイドは一般的に不安定な系で、粒子表面の電荷密度や溶液の電解質濃度を変化にさせると、分散したり、凝集したりする。 この分散・凝集のメカニズムを以下に説明する(各式の誘導はⅡ.解説(B)を参照)。 疎水コロイドの分散・凝集の現象については、粒子の荷電表面による電気二重層による反発力作用および粒子内の構成原子・分子間 のvan der Waals引力作用の相反する作用によって理論的に説明することができ、これをDLVO理論という。「DLVO」とは、旧ソ 連の化学者であるDerjaguinとLandau、オランダの化学者であるVerweyとOverbeekの4人の研究者の頭文字に由来している。 (1) 拡散電気二重層 図Ⅰ-5・Aに示すように、電解質溶液中に分散している荷電粒子の界面近傍の溶液側は拡散電気二重層が形成される。この二重 層は、次の相反する2つの作用によって説明される。以下、z-z型対称電解質の溶液とする。 (1) 静電気力によって界面電荷(例えば、正の電荷)に対して、反対符号のイオン(対イオン)は界面へ近づくように引力が 働き、同符号のイオン(同イオン)は遠ざかるように斥力が働くので、図Ⅰ-5・Cに示すように界面近傍では対イオン個 数(n–)と同イオン個数(n+)との濃度差Δn(= n+ – n–; < 0)が生じる。 (2) 一方で、液中では正負の両イオンは熱運動による拡散力がそれらの濃度差Δnを減少させるように働く。 粒子界面から遠ざかるにつれて静電気力が減衰するのに対し、拡散力は一定であるので、遠く離れたところでは、拡散力 が支配的となり正負イオンの個数濃度は等しくなる(n+ → n∞、n– → n∞、Δn → 0;n∞は母液中の正負のイオン 数)。 (2) 電気・拡散二重層を示す基本式 正負の符号が異なるイオン個数が異なると、溶液系のある無限小の体積Δv[m3]が電荷を有するようになり、その密度ρ[C/m3] は次式で示される。 ρ = zeΔn/Δv (Ⅰ-1) また、拡散層における電荷ρと電位Ψの関係は、次のPoissonの式で示される。 ∇2Ψ = – ρ/ε (Ⅰ-2) ただし、ε = εrεo、ε:溶媒の誘電率、εs:溶媒の比誘電率、εo:真空の誘電率 式(Ⅰ-1)と式(Ⅰ-2)の関係より、界面電位Ψoとする球形の粒子表面の法線方向をx軸とし、界面からの距離 x[nm]における電位 は、次式で近似される。 Ψ(x) = Ψoexp(-κx) (Ⅰ-3) ここで、κ は式(Ⅰ-9)で示される。 Ψ(x)の分布は、図Ⅰ-5・Bに示すような二重層電位Ψの減衰として表すことができる。 なお、界面電位Ψoは一般に測定困難な量であって、測定可能な「すべり面」における電位(ζ-電位)で近似することが多い。す べり面とは、粒子と液とが相対的に動くときの境界面である。 図Ⅰ-5 荷電粒子の電気二重層と2粒子の接近のモデル図A:電気二重層のモデル、B:固液界面からの距離と電位、C:固液界面からの距離とイオン個数の濃度、D:粒子同士が接近したときの電気二重層の重なり 留意事項 吸着性イオン(界面活性剤イオン、高分子イオン、高原子価イオン、錯イオンなど)が存在すると、その濃度に応じた吸着が起 こる。吸着イオンの大きさに相当する厚さの吸着層が形成され、その吸着層と溶液との界面に電位(Stern電位Ψδという)が 発生する。対イオンはその外側に分布するので、Ψの変化はΨoではなくて、Ψδから出発する(Ⅱ.解説(B)-図B-1(C)を参 照)。本章では、吸着性イオンが共存しないコロイド系について議論を行う。 (3) 接近2粒子間に働く力とその系の自由エネルギー 図Ⅰ-5・Dに示すように、球状で半径 aの2つの荷電粒子が接近して、それらの表面の最短距離(2粒子の中心を結ぶ直線とそ れらの粒子表面との交点間の距離)をhとする。 粒子同士が接近したとき、斥力PR[N](>0)および引力PA[N](<0)の相反する力が働き(添字、R: repulsion、 A:aggregation)、これらの合力は次式で示される。合力P<0であれば、粒子はより接近するように凝集力が働く。合力P >0であれば、粒子は遠ざかるように分散力が働く。 P(h) = PR(h) + PA(h) (Ⅰ-4) 斥力 PRの原因は、疎水コロイドの分散している溶液で、電気二重層を持つ2つのコロイド粒子が接近すると、図Ⅰ-3に示した ように電気二重層内の対イオンの重なりにより浸透圧が増大するので、コロイド粒子には反発力が働くからである。 一方で、引力 PAの原因は、コロイド粒子同士がかなり近くまで接近したときには、粒子間にvan der Waals力に起因する粒 子間引力が働くからである。 しかし、その粒子系において、「凝集するか、分散するか」は、その系が自由エネルギー的に「安定であるか、不安定である か」によって決まる。コロイド2粒子系における自由エネルギーVは、斥力および引力に起因するエネルギーVRおよびVAの和 として、次式で示される。 V(h) = VR(h) + VA(h) (Ⅰ-5) 2粒子間に働く合力P(h)とその系の自由エネルギーには次の関係がある。 dV(h)/dh = P(h) または V(h) = ∫|P(h)|dh (h = ∞ → h) (Ⅰ-6) ただし、V(∞) = 0 ここで、Ⅱ.解説(B)で詳述する電気二重層モデルの条件下では、半径 a[m]の2個の荷電粒子が、遠くから粒子界面距離 h[m] に接近したときの合力P(h)および自由エネルギーV(h)は、次式で近似的に示される。 P(h) = 2πaεκΨo2 exp(-κh) – aA/(12h2) (Ⅰ-7) V(h) = 2πaεΨo2 exp(-κh) – aA/(12h) (Ⅰ-8) κ2 = 2nz2e2/(εkT) (Ⅰ-9) κ = 3.3×109z√C [/m] (at T = 298K) (Ⅰ-10) なお、式(Ⅰ-7)~式(Ⅰ-10)において、Ψo:粒子-水界面における電位[V]、ε:水の誘電率(7.08×10-10[N/m2/C2]、 25℃)、A:Hamaker定数、z:z-z型対称電解質の価数、n(= n∞ = 1.0×103C):単位体積中の電解質イオン個数 [1/m3]、C:電解質濃度[mol/L]である。 (4) 疎水コロイドの凝集と分散 一般に系の自由エネルギーVの値が低いほど、その状態はより安定となる。2つの荷電粒子が接近したときの表面間距離 hに対す る自由エネルギーV(h)と粒子間に働く合力P(h)の関係の事例を図Ⅰ-6に示す。 一般に、V(h)の極大値Vmax(dV(h)/dh = P(h) = 0 → PR = PA)が存在し、凝集系と分散系の境界にエネルギー障壁が現れ る。粒子が接近したとき、「分散 → 凝集」へ移行するには、このエネルギー障壁を越える活性化エネルギーが必要となる。コロ イド粒子はブラウン運動をしており、そのエネルギーはkT(= 26meV、25℃)を用いて議論される。Durhanによれば、半径 100nm以上の粒子について、Vmax>15kTでは、ブラウン運動によってこの障壁を越える確率が極めて低く、長期間にわたっ てコロイド状態は安定に存在する。Vmax<15kTでは、この障壁を越える確率が高くなりコロイド系は不安定となり緩速凝集が 進行し、さらにVmaxが消失すると急速凝集が起こることとなる。 留意事項 本章での説明はコロイド状態の安定性をエネルギー的に論じているが、その状態が時間的にどの程度維持できるかについては、 別の問題である。コロイドの凝集速度については、Ⅱ.解説(E)を参照されたい。 図Ⅰ-6 球形・同サイズ・同荷電の2粒子系に働く力と自由エネルギーP:粒子間に働く合力、PR:静電気的反発力、PA:van der Waals引力、V:2粒子系の自由エネルギー{ただし、V(∞) = 0 とする}、VR:静電気的エネルギー、VA:van der Waalsエネルギー、a:粒子半径、h:2粒子表面の最短距離、Ψo:表面電位(Stern電位)、A:Hamaker定数、1/κ:二重層の厚さ(Debye長さ) 具体的計算:図Ⅰ-6については、Excelファイルをダウンロードし、具体的に試算するとよい。なお、ページトップの目次-付 録に記載のファイルも同じものである。 学生や初心者の方は、同ファイルの各パラメータに具体的な数値を記入して、Vmaxは「どの因子によって大きく影響される」 か実感されたい。そして、「その因子が変化する原因はどのような理由によるもの」か考察することが、現実の水浄化プロセス の開発・改善や維持管理において役立つこととなろう。 3.2 コロイドの分散・凝集の因子 コロイド粒子が長時間にわたって安定であるか、凝集するかは、コロイド系の自由エネルギーの極大値Vmaxの高さに依存すること を前節で述べた。ここでは、Vmaxの高さに及ぼす主な因子について述べる。Vmax (= V(ho))においては、P(ho) = 0であるので、 式(Ⅰ-7)および式(Ⅰ-8)より、次式が得られる。 Vmax = 2πaεΨo exp(-κho) (1 – κho) (Ⅰ-11) 上式と式(Ⅰ-10)から、a = 一定、T = 一定のとき、Vmaxは、粒子界面の電位Ψoおよび電解質の電荷 zとその濃度Cに大きく依存す ることが分かる。 (1) 粒子表面電位 Ψoとエネルギー障壁 Vmaxの高さ 界面電位Ψoを変化したときの、各Ψo値に対する自由エネルギーV(h)と距離 hの関係を図Ⅰ-7に示す。表面電荷が高くなると、 Vmaxは高くなる。 Ψo<15mVでは Vmax<10kTとなり、ブラウン運動エネルギーによってエネルギー障壁を越える確率が高くなり、分散系は不 安定で凝集が起こることが推定される。逆に、Ψo>25mVでは Vmax>40kTとなり、分散→凝集への活性化エネルギーが高 く、凝集速度は極めて遅くなり分散系は安定であることが推定される。 図Ⅰ-7 球形・同サイズ・同荷電の2粒子系の自由エネルギーに対する表面電位の効果記号等の説明および計算については、図Ⅰ-6と同じ。 (2) 酸化物/水酸化物の表面の等電点 酸化物/水酸化物の固体粒子を水に分散させると、その表面は水和して、次の化学平衡を起こす。 -O-M=O(粒子表面)+ H2O → -(OH)-M-OH -M-OH + H+ ⇄ -M-OH2+ (低pH) -M-OH + OH– ⇄ -M-O– + H2O (高pH) 低pHでは水素イオンH+と、高pHでは水酸化物イオンOH–と粒子表面-M-OHとの平衡反応(不可逆的な化学吸着ではない) が生じ、正または負に帯電する。表面電荷が消失するpHoが高・低pHの中間で存在し、このpHo値を等電点(iso-electric point, iep)という。任意のpHにおける表面電位Ψoはネルンストの式から、次式で示される。 Ψo = -ne(pH – pHo)/(kT) (Ⅰ-12) = – 59(pH – pHo) [mV] (at 25℃) 以上のことから、酸化物/水酸化物粒子の分散・凝集はpHに大きく依存することとなり、凝集操作においてpHは正確に調整す る必要がある。表Ⅰ-4に、酸化物/水酸化物の表面の等電点を示すpHoを示す。 表Ⅰ-4 酸化物/水酸化物の表面の等電点sp:流動電位法、eo:電気浸透法、mep:電気泳動法文献(古澤, 2004)のデータをpHo値(測定方法によって、同じ物質でも値が異なるが)の順に並び替えた。訂正:γ-Al2O4 → γ-Al2O3 (3) 電解質添加によるエネルギー障壁の低下 前節で述べたように酸化物粒子などではpH調整により表面電荷を制御できるが、現実には溶液のpHを特定値に保つ必要もあ る。また、コロイド粒子間に働く van der Waals力の大きさは、コロイドを構成する内部の原子・分子に固有のもので粒子表 面の性状に無関係であるので、溶液(分散媒)の条件によって変えることができない。 一方で、先に示した図Ⅰ-5・Dから分かるように、粒子・溶液界面の電気二重層が厚いほど、粒子同士が接近したときの重なり 領域が広くなり、コロイド粒子間に働く反発力が増加する。 そこで、疎水コロイドが分散している溶液に電解質を加えると、上式(Ⅰ-10)で示したように、その濃度が高いほど、電気二重層 の厚さ(1/κ)は小さくなり、粒子間の反発力は減少する。さらに添加する電解質イオンの価数zが大きくなると、その効果は格 段に高くなる。 図Ⅰ-8に塩化ナトリムの添加によるエネルギー障壁Vmaxへの効果を示す。この事例では、NaCl濃度>100mmolでは、エネル ギー障壁Vmax<15kTであるので、コロイド系は不安定となり、粒子の凝集が進行することが推定される。 なお、凝集に必要な電解質の濃度は、解離イオン価数zの6乗に反比例し、多価電解質の凝集効果が極めて効果的であることが実 験により分かっているが、理論的にも説明できる(Ⅱ.解説(D)を参照)。 図Ⅰ-8 球形・同サイズ・同荷電の2粒子系の自由エネルギーに対する電解質の添加効果記号等の説明および計算については、図Ⅰ-6と同じ。4.親水コロイドの塩析 親水コロイドのコロイド粒子表面には、親水性の官能基(-OHや-COOH、-CO-、-NH2など)を多数有している。上記図Ⅰ-4 に示したように、これらの親水基が水素結合によって水分子を粒子表面に強く引き付けているために、水和水層が立体障害になって コロイド粒子同士の凝集は妨げられている。したがって、親水コロイドを凝集させるためには、表面での水素結合を切り、コロイド 粒子を覆っている水和水を表面から剥ぎ取らなければならない。 電解質をコロイド溶液に加えると、水中でイオンに電離する。これらの電離イオンは、親水基よりも強く水分子と引き合うので、親 水コロイドに塩化ナトリウム NaClなどの塩を加えれば、理論上は水和水を失って、親水コロイドは沈殿するはずである。しかし、 NaCl濃度を1mol/Lぐらいにしても、なかなかコロイド粒子は沈殿しない。水溶液には約1000/18 ≒ 56mol/Lの水分子が存在為て いるのに対して、塩濃度が1mol/L程度ではイオンの数が少なすぎて、親水基と水分子の水素結合を切るに至らない。親水コロイドに ついては、少量の塩を加えただけでは凝集が起こらず、NaCl濃度が5~10mol/Lぐらいになって、初めて親水基と水分子の水素結合 が切れ、親水コロイドの凝集が起こる。このように親水コロイドに多量の電解質を加えて凝集させることを、一般的に塩析(salting out)という。 セッケンのコロイド溶液に飽和食塩水を加えてセッケンを析出させたり、タンパク質のコロイド溶液である豆乳にニガリMgCl2や硫 酸カルシウムCaSO4を加えて豆腐を作るのは、塩析を利用したものである。 (1) 保護コロイド 疎水コロイドに親水コロイドを加えると、疎水コロイドが凝析しにくくなることがある。このときに加える親水コロイドを保護コロ イド(protective colloid)という。 これは、疎水コロイドの周りを親水性の保護コロイドが取り囲み、さらにその周りを水分子が水和しているため、疎水コロイドの表 面が親水化されるからである。保護コロイドを加えると、疎水コロイドは電解質に対して安定になる。例えば、疎水性である赤色ア ルカリ性金コロイドに対して、ゼラチンは強い保護作用を示す。その他の例としては、墨汁のニカワやマヨネーズの卵黄は、代表的 な保護コロイドである。ただし、この保護作用の強さは物質の種類だけでなく、pHや調整法などにより著しい影響を受ける。 5.会合コロイドとミセル 界面活性剤は、生活・産業において広く活用されている。水浄化においても、懸濁水の凝集剤として利用されている。詳しくは Ⅱ.解説(G)に記載しているが、ここではその代表的な性質を概説する。 5.1 界面活性剤とミセル ミセル(micelle)とは、界面活性剤の分子またはイオンの集合体のことである。界面活性剤は、分子内に親水基と疎水基の両方を持つ ため、両親媒性分子とも呼ばれる。次の図Ⅰ-9に代表的な界面活性剤であるステアリン酸ナトリウムC17H35COONaの構造式を示 す。 図Ⅰ-9 ステアリン酸ナトリウムC17H35COONaの構造式と略号 水溶液中の界面活性剤の濃度を上げていくと、水溶液中で界面活性剤が集合して、大きなミセルを形成する。少量の界面活性剤を添 加した水溶液中では、ミセルは形成されない。 界面活性剤分子は分子内に疎水基があるため、水中では不安定である。水はその分子間の凝集力が大きいため、疎水基を水からはじ き出そうとする傾向がある。図Ⅰ-10・Aのように、少量添加した界面活性剤の大半は、空気-水界面へ移動し疎水基を空気側へ向け て配置される。また、水と油のような状況でも、界面活性剤はその界面へと移動・配置される。界面活性剤の界面吸着能はその重要 な物性の1つである。界面活性剤がミセルを形成し始める濃度を臨界ミセル濃度(critical micellar concentration、cmc)といい、 この濃度は、コロイドであるかないかを区別する重要な値である。 水溶液中の界面活性剤の濃度を上げていき、cmcに達すると、それ以上は界面に存在できない状態となる。この状態は、溶液の表面 全体が界面活性剤分子で覆われ、図Ⅰ-10・Bのように、表面配置が飽和してしまった状態である。さらに濃度上げていくと、行き場 のなくなった界面活性剤は分子同士で疎水基を重ね合わせ、親水基を外側(水側)に向けて互いに集まることにより、図Ⅰ-10・Cのよ うに安定な集合体を形成して水中に分散する。この集合体がミセルである。 図Ⅰ-9 ステアリン酸ナトリウムC17H35COONaの構造式と略号 このミセルの大きさと形状は、直径が分子の長さの約2倍程度の球状粒子であり、コロイドの範囲に入る。したがって、界面活性剤の 濃度がcmc以上になって初めて、界面活性剤の水溶液はコロイドになることができる。界面活性剤の水溶液は、cmc以下の濃度では コロイドにはならないので、濃度によってコロイドになったり、そうでなくなったりする興味深い性質を持つ。濃度をcmc以上にす れば、このミセルは自然と生成する。 5.2 不溶性物質の可溶化 界面活性剤を使うと、水と油のように互いに混ざり合わない物質の一方を、他方に分散させることもできる。これは、界面活性剤が ミセルを形成して、ミセル内にその物質が取り込まれるからである。図Ⅰ-11・Aは、ミセル内に油相が取り込まれ、水中に油が分散 している事例である。液体に溶けにくい物質が界面活性剤の存在下でその液体に溶けるようになる現象を可溶化(solubilization)とい う。 界面活性剤溶液への可溶化は、臨界ミセル濃度以上で起こる。この場合の可溶化量と界面活性剤の濃度との間には、一般的に図 Ⅰ-11・Bのような関係がある。このグラフから、逆に臨界ミセル濃度を間接的に求めることもできる。 図Ⅰ-11 界面活性剤の添加による油性物質の水中への可溶化A:O/Wマイクロエマルジョンのモデル(●:油の粒子)、B:界面活性剤の濃度と油の可溶化量 ミセルには、水相(W)に油相(O)が分散するO/Wエマルジョンと、油相に水相が分散するW/Oエマルジョンがある。O/Wの代表例は 食器に付着した油の可溶化で、W/Oの代表例は油井原油中に含まれる水分である。 可溶化量が増すと、ミセルは膨らんでいく。光の散乱状態は、ミセルが膨らむと増大し、液は半透明になって乳光を発したり、やや 濁って見えたりする。そこで、この現象を界面活性剤の乳化作用(emulsifying action)という。マヨネーズや乳液などには界面活性 剤が使われており、この乳化作用のために、白く濁って見える。 前述した水-油-界面活性剤の3成分系であるが、この系に中級アルコール(炭素数4~8)を補助剤として添加し4成分系にすると、図 Ⅰ-12に示すように、水に対して多量の油を(O/W)、または、油に対して多量の水(W/O)を含む広い組成範囲のエマルジョンを つくることができる。 図Ⅰ-12 オクチル硫酸ナトリム-ヘキサノール-デカン-食塩水の4成分系でのマイクロエマルジョン(ME)の生成6.コロイド溶液の物性 6.1 透析 コロイド粒子は、ろ紙の穴より小さいので、ろ紙を素通りして分離できない。しかし、セロハン膜やコロジオン膜の穴よりは大きい ので、これらの半透膜を通過できない。一方で、コロイド粒子より小さなイオンや分子は、このセロハン膜の穴をも通ることができ る。そこで、このような装置を使うことで、小さなイオンや分子を除き、コロイド粒子のみの溶液にすることが可能となる。この操 作を透析(dialysis)という。 透析を利用した水酸化鉄(III)・Fe(OH)3のコロイド溶液の作成を説明する。沸騰水に塩化鉄(III)・FeCl3水溶液を加えると、加水分解 反応が起こり、赤褐色のFe(OH)3のコロイド溶液が作成できる。沸騰水での反応の理由は、高温のために加水分解反応が急激に進む ので、多数に生成したFe(OH)3の小さな結晶核が大きな沈殿粒子まで成長できず、コロイド粒子のサイズで成長が停止しているから である。このコロイドは、溶液中の水素イオン・H+または鉄(III)イオン・Fe3+が表面に吸着しているので、正に帯電した疎水コロイ ドとなっている。 FeCl3 + 3H2O → Fe(OH)3↓ + 3HCl 生じたコロイド溶液を半透膜であるセロハン袋に入れて、流水中に浸して透析を行うと、水素イオン・H+や塩化物イオン・Cl–は拡 散によりセロハン膜を通過して流出していく。しかし、Fe(OH)3のコロイド粒子は半透膜を通過できず、セロハン膜内に留まる。こ の操作によって、Fe(OH)3のコロイドをセロハン袋中に精製することができる。 写真Ⅰ-1 (左)赤褐色の水酸化鉄(III) ・Fe(OH)3コロイド溶液、(右)セロハン膜による水酸化鉄(III)の精製 血液透析 透析を有効に利用しているのが、私たちの体の中にある腎臓である。腎臓には、血液中に含まれる尿素(NH2)2COなどの老廃 物を取り除く働きがある。腎臓病により、腎臓の機能が低下してくると、老廃物を体外に排泄できなくなり、尿毒症により生命 の危機に陥ることとなる。これを回避するために、人工透析が行われる。人工透析には、図Ⅰ-13に示すような血漿分離器が用 いられている。 まず、体外に取り出した血液を血漿分離器に通して、血球成分と血漿成分に分離する。赤血球や白血球などの血球成分は透析膜 を通過できないが、小さい分子である尿素(NH2)2COは透析膜を通過するので、これらを分離することができる。このとき分 離された血漿の代わりに、新鮮な血漿もしくはアルブミン溶液を補充する。 人工透析は、半透膜としての作用が弱った腎臓の働きを、このようにして人工的に行う治療法である。 図Ⅰ-13 血液透析の原理 6.2 光学的性質 コロイドは必ずしも濁っているとは限らず、透明または半透明なものも多い。しかし、透明に見えていても、コロイドの横から強い 光を当てると、光の通路が光って見える。これは、コロイド粒子の大きさが可視光の波長(350~700nm)とほぼ等しいため、その 表面で光がよく散乱されるからである。この現象をチンダル(Tyndall)現象といい、この光をチンダル(Tyndall)光という。これ はコロイドの特性の1つであり、チンダル現象の有無により、コロイドを見分けることが可能となる。 着色物質は光を吸収する。吸収の極大波長は分子・イオン・結晶では、物質に固有なもので、それぞれ固有な色を呈している。しか し、コロイドの色は物質に固有なものではない。 光の散乱と吸収の度合いを一つにまとめると、 ln Io/I = (ε+τ)・l ここで、Io/I は入射光/透過光の強さ、l は測定セルの厚さ、ε/τ は吸収係数/濁度である。ε = 0 のときにThydall式、τ = 0 のと きにLambert式となる。測定セル中のコロイド粒子数をN、粒子半径をaとすると、 ε = πNa2QA τ = πNa2QS (Ⅰ-13) となる。QA/QSは吸収因子/散乱因子といわれ、粒子半径 a、測定波長λ、屈曲率などの関数である。 粒子による散乱には、レイリー(Rayleigh)散乱とミー(Mie)散乱がある。レイリー散乱は、光の波長よりも小さいサイズの粒子 による散乱現象である。ミー散乱は、光の波長程度のサイズの粒子による散乱現象である。粒子のサイズが大きくなるとミー散乱と 幾何光学の双方の手法による計算結果が類似するようになる。 散乱波の波長λと散乱粒子の直径 d(= 2a)に関するサイズパラメータとして、 α = πd/λ があり、α≪1 はレイリー散乱、α~1 はミー散乱、α≫1 は幾何光学近似で表現できる。 写真Ⅰ-2 チンダル現象の事例 上式で示したように、チンダル現象は光の散乱が原因で、原子やイオンのような小さな粒子では光を散乱しないが、コロイドぐらい の大きさの粒子では光をかなり強く散乱する。なお、疎水コロイドのチンダル現象は比較的はっきり現れるが、親水コロイドのチン ダル現象はあまりはっきり現れない。 チンダル現象は、主にミー散乱によるものが大きい。レイリー散乱は、光の波長の依存性が高く、波長の短い青色の光は、赤色の光 よりも強く散乱される。長い波長の光は粒子による散乱が少なく、波長の短い光ほど粒子にょる散乱が起きやすい性質がある。空が 青いのは、レイリー散乱より説明できる。これは、大気中の微粒子により、青色の光が強く散乱されるからである。また、ミー散乱 は、波長の依存性が低いので、どの波長の光も同程度に散乱する。雲が白く見えるのは、ミー散乱が原因である。 表Ⅰ-5 ミー散乱とレイリー散乱の違い 6.3 微粒子の運動 微粒子は、その密度が媒質のそれよりも大きい場合、重力による下降運動するとともに、熱運動としてのブラウン運動も行ってい る。この両運動の兼ね合いで、粒子全体としての運動が決まる。 (1) 沈降 重力 Fgで下降する場合には、媒質から抵抗 Ffを受ける。上下方向の流れがない媒質中では、FgとFfがつり合うと粒子は等速 uで下 降し、これを沈降という。 粒子の半径 aの球とすると、浮力を補正した重力は、 Fg = (4/3)πa3(ρ – ρo)g (1) ρ・ρo:粒子・媒質の密度、g:重力加速度 抵抗力は媒質の摩擦抵抗で、摩擦抵抗をf、下降速度を uとすると、 Ff = f・u (2) 球状粒子は剛体でその濃度が希薄な場合(自由沈降)には、媒質の粘度をηとすると、 f = 6πηa (3) Fg = Ffの場合には、上記3式の関係より、下降速度 uは次式で示される。これをStokesの式という。 u = 2a2(ρ – ρo)g/(9η) (Ⅰ-14) なお、高速回転で遠心力を利用する場合には、重力加速度 g → 遠心力の加速度 ω2x(ω:角速度、x:回転中心から粒子までの距 離)を用いる。この方法は小さい粒子の沈降・分離に用いられる。 (2) ブラウン運動 イギリスの植物学者であるRobert Brownは、1827年に植物の花粉から生じた微粒子が、不規則な運動をすることを発見した。し かし、発見当時、この現象は「花粉の生命力に基づくものである」と誤解されていた。Brownは、これをブラウン運動(Brownian motion)と名付けた。その後、他の微細な粒子でも、同様の現象が起こることが確認されたが、長い間その原因は不明のままであっ た。 1905年に相対性理論で有名なAlbert Einsteinが、ブラウン運動の原因を突き止めた。Einsteinは、熱運動する媒質分子の不規則な 衝突により、ブラウン運動が引き起こされるということを、統計力学を駆使して理論的に説明した。媒質に浮かぶ微粒子は、各瞬間 毎に非常に多くの媒質分子に衝突されているが、その衝突はデタラメに起こるので、ある瞬間に微粒子が受け取る運動量はつり合っ ていない。この衝突の不均衡のために、粒子が動くのである。 ブラウン運動は粒子の不規則な熱運動であるから、統計的に計算できる。時間 tで z軸方向へ動く距離の平均 は、次式となる。 <x> = (2Dt)1/2 (1) ここで、D は粒子の拡散係数である。これをEinsteinのブラウン運動という。さらに、Einsteinによると、 D = kT/f (2) f は摩擦係数で、前節<沈降>の式(3)を用いて、次に示すEinstein-Stakesの式が得られる。 D = kT/(6πηa) (Ⅰ-15) これを式(1)に代入すると、 <x> = [kTt/(3πηa)]1/2 (Ⅰ-16) が得られる。 ブラウン運動による粒子の移動は、粒子の個数濃度の濃い方から希薄な方へと起こる。上式によると、ブラウン運動による拡散の速 さは、粒径 aが小さいほど速く、また粒子の平均速度 <x>はボルツマン分布に従い、温度 Tが高いほど拡散は速くなる。 図Ⅰ-14 ブラウン運動のシミュレーション (3) ブラウン運動と沈降 泥水のようなコロイドにおいて、泥の微粒子がなかなか沈降してこないのは、微粒子がブラウン運動をしているからである。重力に よって微粒子が沈降しても、ブラウン運動によって、微粒子は希薄になった上部へと拡散する。コロイド粒子が沈降して下部に沈積 してしまうか、液中に浮遊しているかどうかは、媒質の粘度にもよるが、主として粒径に依存する。粒径が大きいものは沈降して、 粒径が小さいものは拡散する。 式Ⅰ-14と式Ⅰ-16から計算した、水中における球形粒子(ρ/ρo = 2.5)のブラウン運動と重力沈降の比較を図Ⅰ-15に示す。粒子半 径が100nm付近(ao)で、移動距離と沈降速度が等しくなる。粒子径 a≪aoではブラウン運動が支配的となって粒子の分散状態が 継続し、a≫aoでは粒子は沈降することとなる。 a = 1μmレベルの粒子の沈降速度は3.6μm/sとなり、1mの深さに沈殿するのに3.2日を要する。上下左右の流れのある国内河川で は、雨天時の泥水を構成する微細な粒子は沈降することなく海に流れ込むこととなる。 図Ⅰ-15 水中における球形粒子のブラウン運動と重力沈降の比較a:粒子の半径[nm]、u:重力による沈降速度[m/s]、<x>:ブラウン運動による平均移動距離[m/s] 6.4 電気泳動 表面が正あるいは負に帯電しているコロイド粒子は、電極を入れて電圧をかけると、表面電荷と反対符号の極へと移動する。これを 電気泳動(electrophoresis)という。この現象から、コロイド粒子の表面が、正負どちらに帯電しているのかが決定できる。 例えば、水酸化鉄(Ⅲ)・Fe(OH)3コロイド溶液を電気泳動させると、Fe(OH)3のコロイド粒子は、ゆっくりと陰極の方へ移動する ので、Fe(OH)3のコロイド粒子は、正に帯電していることが分かる。一般に正に帯電しているコロイド粒子を含むコロイドを正コロ イド(positive colloid)、負に帯電しているコロイド粒子を含むコロイドを負コロイド(negative colloid)という。 粒子の移動は、粒子の大きさや形状、表面電荷、加えた電圧、pH、温度などによって影響され、異なるコロイド粒子を、移動速度の 差を使って分離することもできる。これは、タンパク質・DNA断片の分離・分析などによく用いられる。なお、疎水コロイドの電気 泳動の移動速度は比較的大きいが、親水コロイドは水和水のために、移動速度は小さい。 写真Ⅰ-3 DNA断片の電気泳動分析-活性汚泥・細菌群の16S-rDNA解析事例参考文献1) 池上 徹(栗田工業KCRセンター):水処理教室-凝集処理、https://kcr.kurita.co.jp/wtschool/012.html2) 化学工学協会編:化学工学便覧、丸善、19783) 北原 文雄・渡辺 晶:界面電気現象-基礎・測定・応用-、共立出版、19724) 北原 文雄:界面・コロイド化学の基礎、講談社、19945) 作花 済夫:ゾル-ゲル法の科学、アグネ承風社、19886) 小林 幹雄・他4名共編:数学公式集:共立出版、20057) 長谷川 裕也:コロイド化学、http://sekatsu-kagaku.sub.jp/colloid.htm8) 福田 清成・中垣 正幸:コロイド化学の基礎、大日本図書、19699) 古澤 邦夫:ぶんせき、5、247-254(2004)10) 粉体工学会編:液相中の粒子分散・凝集と分離操作、日刊工業新聞社、201011) 松村 淳司:界面・電気化学講義、http://res.tagen.tohoku.ac.jp/~liquid/MURA/kogi/kaimen/kaimen2002/2002-6.pdf12) 用水廃水便覧編集委員会編:用水・廃水便覧、丸善、197313) Alonso, M. and E. J. Finn, E.J.: University Physics-Volume Ⅱ Field and Waves, Addison-Wesley Publoshing Co., 196714) Bergdtrom, L.: Hamaker Constants of Inorganic Materials, Advances in Colloid and Interface Science, 70, pp.125- 169, 199715) Derjaguin, B.V.: Kolloid Z. (in German). Vol.69, No.2, pp.155–164, 193416) Hamaker, H.C.: Physica IV, No.10, 1058, 193717) Otterwill, RH & A. Watanabe: Kolloid. Z., Vol.170, p.133, Fig.1, p.135, Fig.4( 1960) Ⅱ.解 説解説(A) 粒子界面の静電気現象粒子に特異吸着しない成分から構成されるz-z型電解質(電解質)液中に、荷電粒子(例えば、正に帯電)が存在するとき、粒子表面近傍の溶液は電気的中和を保つため、図Ⅰ-5・Cに示したように、界面電荷と反対符号のイオン濃度(n–:単位体積中の負イオン個数[1/m3])が高く、逆に同符号のイオン濃度(n+:単位体積中の正イオン個数)が低くなって、正と負のイオンの個数濃度差Δn(= n– – n+)が生じる。一方で、熱運動による拡散作用によって、正負のイオンは同一の個数濃度になろうとする。このように相反する静電気作用と熱拡散作用が働くが、界面から離れるにしたがって静電気作用は減衰して、ついには拡散作用のみとなるので、表面から遠く離れたところでは正負のイオン個数濃度は同一(n+ = n– = n∞)となり、正負イオンの濃度差Δnは消失する。<イオン数濃度> 拡散電気二重層内において電位Ψ[V]を示すある微少体積Δv中の正負イオンの個数濃度は、Boltzmann分布に従うので、それらの個数濃 度は次式で示される。 n+ = n exp[- zeΨ/(kT)] n– = n exp[zeΨ/(kT)] (A-1) n(= n∞):母液中の電解質の個数濃度[/m3]、 n+・n–:拡散二重層内における正・負イオンの個数濃度[/m3]、 z:z-z型電解質のイオン価数、e:素量電荷(1.60×10-19[C])、 k:ボルツマン定数(1.38×10-23[J/K])、T:絶対温度[K]<Poisson式> 拡散層内における電位Ψの変化は、次のPoissonの式で示される。 ∇2Ψ = – ρ/ε (Ⅰ-2) ρ:電荷密度[C/m3]、ε:水の誘電率 (7.08×10-10[N/m2/C2]、25℃)<電荷密度> 上式(Ⅰ-2)に示す電荷密度ρは、単位体積中の正負イオンの個数差にイオン電荷量zeを乗じて求められるので、式(Ⅰ-2)中の ρ は、式(A- 1)を用いて次式で示される。 ρ = ze(n+ – n–) = nze{exp[-zeΨ/(kT)] – exp[zeΨ/(kT)]} = – 2nze・sinh[zeΨ/(kT)] (A-2)<電位変化> ここで扱う電気二重層モデル(a≧1/κ)では界面を近似的に平面として扱うので、界面からその法線方向の溶液側にx軸をとると、式(A- 2)を式(Ⅰ-2)に代入すると、次式が得られる。 d2Ψ(x)/dx2 = (2nze/ε)×sinh[zeΨ(x)/(kT)] (A-3) 式(A-3)を x = ∞ (Ψ = 0) ~ x = 0 (Ψ= Ψo) の範囲で積分すると、次式が得られる。 tanh[zeΨ(x)/(4kT)] = γexp(-κx) (A-4) γ = tanh[zeΨo/(4kT)] (A-5) 式(A-4)を変形すると、界面電位Ψoを有する荷電粒子の表面から距離x(x≦a)における電気二重層の電位Ψ(x)は、次式で示される。 Ψ(x) = 2kT/(ze)・ln[1 + γexp(-κx)]/[1 – γexp(-κx)] (A-6) 式(A-6)が求めるΨ(x)であるが、特に電位の低いzeΨo≪4kT(25℃で4zeΨo≪104mV)であるならば、式(A-6)のln[1 + γexp(-κx)]/[1 – γexp(-κx)] = 2γexp(-κx)となる(Debye-Hukel近似)ので、次式のように簡略化される。 Ψ(x) = 4kT/(ze)・γexp(-κx)] (A-7) したがって、式(A-3)は、次式のように簡易化される。 d2Ψ(x)/dx2 = κ2Ψ(x) (A-8) 式(A-8)を、式(A-4)を求めた同じ範囲で積分すると、式(A-4)の近似式として、次式が得られる。 Ψ(x) = Ψo exp(-κx) (Ⅰ-3)<留意事項> 電解質溶液中の分散粒子について、Boltzmann分布の式(A-1)およびPoissonの式(Ⅰ-2)を用いて正確なΨ(x)を求めることは困難を伴う ことから、球状粒子に限らず、様々なモデルに基づくΨ(x)を示す式が提案されている。また、実際に固液界面の構造は複雑であること、 また、導電性電極では固液界面の電位Ψoが測定可能であるが、分散粒子の表面電位の測定は困難である。実際に測定可能な電位は、荷電 粒子の動電現象による ζ-電位(図B-1、参照)である。また、現実の界面現象は、無機・有機の共存物質やpHによって様々な影響を受 け、厳密な定量的な解析は複雑となる。したがって、水浄化の現場での凝集分離およびその操作条件は、ジャーテストによって実験的に 確認され、その操作条件が決定される。 以上のような理由により、水浄化分野における分散粒子の数量的取扱いにおいて、疎水性コロイド粒子に対しては、その挙動や傾向は近 似式(Ⅰ-7)・(Ⅰ-8)で概略的な説明が可能である。疎水性粒子についての数量的取扱いは、前編Ⅰ-3や本解説(A)・(B)で記載している が、疎水性でない粒子の界面近傍の数量的扱いについては、複雑となるので省略する。<電気二重層の厚さ> κ[/m]は二重層電位ψの変化を決める重要な量で、1/κ[m]は電位ΨがΨo/exp(1)に低下す表面からの距離を示すので、二重層の拡がりの 指標となり、1/κを二重層の厚さまたはDebye長さという。式(A7)によると、NaCl水溶液では、1mmol/Lで10nm、0.l mol/Lで1nmと 推定される。 z-z型電解質の濃度と電気二重層の厚さを表A-1に示す。 2価・3価の金属イオンは配位水を有し、pHの上昇により酸解離してOH–が配 位した錯イオンを形成し、予想される1/κよりも大きい値となることに留意する(詳しくは、解説(D)-1.電解質効果)。 表A-1 電解質溶液の電気二重層の厚さ解説(B) 疎水性2粒子系の相互作用本解説(B)では、前解説(A)で扱った「疎水コロイド界面の電気二重層」に基づき、水溶液中で2つのコロイド粒子が接近したときの相互作用を数量的に扱う。最初に、コロイド系のモデルと相互作用の結論を示し、この結論に至る説明を行う。なお、コロイドに関する本モデルは、次の条件に限定したものとする。・水溶液内の荷電粒子は球状で、表面電位Ψoとする。ただし、単原子イオンなどÅレベルの小さなイオンが特異吸着している場合には、 Stern電位ΨδをΨoとする(図B-1を参照)。・荷電粒子は疎水性とし、粒子表面に水和層の形成はなく、さらに、特異的に吸着する複雑なイオン(界面活性剤イオン、高分子イオン、 高原子価イオン、錯イオンなど)は共存しないものとする。・水溶液内に共存する正負イオンはz-z価の対称電解質が完全解離したものとする。・電気二重層の厚さ(1/κ)は10nm以下(例えば、NaCl濃度>1mmol/L)で、ここで扱う粒子の半径 aは100nm~1μm程度とすると、2 粒子が接近してそれらの電気二重層が重なったとき、その重なり領域に対応する粒子表面は近似的に平面(具体的には円板)として扱う ことができるものとする(a≫1/κ)。<電気二重層のモデル> 様々な電気二重層モデルが提案されているが、代表的をものを、次の図B-1に示した。 Helmholtzは金属表面の電荷と、これを中和する溶液中のイオンが向かい合って並んでいるいて、これを平行コンデンサーが形成される ようなモデルを考えこれを電気二重層と呼んだ(図B-1・A)。 次に、イオンには熱運動を行って均一に分布する作用が働く。したがって、界面近傍の過剰な対イオンは、重力場内の分散系粒子の沈降 平衡に似た拡散的な分布をとる。このことから、二重層内の電位低下は界面付近で急激で、界面から遠ざかるにつれてなだらかとなる。 これをGouy-Chapmanの拡散二重層のモデルである(図B-1・B)。 しかし、このような拡散二重層のみによって計算した値は、測定値よりも一桁大きく、むしろHelmholtzのモデルによる値がずっと測定 値に近い。この矛盾を解決するために、Sternは金属表面のすぐ近くにはイオンの特異吸着(Stern層)があって、この外側にGouy- Chapmanの拡散二重層が広がっているようなモデルを考えた(図B-1・C・D)。 このような表面の電荷と帯電粒子の固定相、および拡散二重層を総括して界面電気二重層と呼ばれる。本モデルで取り扱う対称は、この 図中の(B)または(C)とする。 図B-1 粒子と電解質溶液の界面近傍における電気二重層のモデル<コロイド粒子の分散と凝集> 一般に、水中の微細粒子はその表面が帯電していて、その静電的反発力によって粒子の凝集作用が阻害され、ブラウン運動により水中に 分散している。ところが、pH変化や電解質添加によって、凝集して粗大粒子(約10μm以上)となるとブラウン運動よりも重力作用が大 きくなって沈降(または浮上)したりする(図Ⅰ-15、参照)。ここでは、ブラウン運動の影響が大きい100nm~1μ前後の粒子をモデル として取り扱う。 粒子間には、静電気的反発力(分散力)PR [N/m2]とvan der Waals引力(凝集力)PA [N/m2]の2つの相互作用が働き、これらの合 力は次式で示される。 P= PR + PA (Ⅰ-4) 一方で、コロイド系の安定性は、その系の状態を分散エネルギーVR[J]および凝集エネルギーVA [J]を総和した自由エネルギーVに依存 する。 V = VR +VA (Ⅰ-5) 本章の冒頭に記載した電気二重層モデルの条件下では、半径 a[m]の2個の荷電粒子が、遠くから粒子界面距離 h[m](<a)に接近した ときの相互作用力P(h)および自由エネルギーV(h)は、次式で近似的に示される。 P(h) = 2πaεκΨo2 exp(-κh) – aA/(12h2) (Ⅰ-7) V(h) = 2πaεΨo2 exp(-κh) – aA/(12h) (Ⅰ-8) κ2 = 2nz2e2/(εkT) (Ⅰ-9) κ = 3.3×109z√C [/m] (T = 298K) (Ⅰ-10) ここで、式(Ⅰ-7)~式(Ⅰ-10)において、Ψo:粒子-水界面における電位[V]、ε:水の誘電率(7.08×10-10[N/m2/C2]、25℃)、A: Hamaker定数、z:z-z型対称電解質の価数、n:単位体積中の電解質イオン個数[1/m3](n = n∞:図Ⅰ-5・C、参照)である。 なお、25℃の水溶液では、電荷質濃度C[mol/L]とすると、n = 103NAC[/m3] (NA:Avogadro定数、6.02×1023[/mol))である ので、式(Ⅰ-9)は式(Ⅰ-10)で示される。 式(Ⅰ-7)・式(Ⅰ-8)に基づいて、試算した結果の事例を図Ⅰ-6~図Ⅰ-8に示した。これらの式の導入過程にあっては様々な近似と簡略化 が行われているが、コロイド粒子の水溶液中における挙動の概要を説明できる。以下に、これらの式の導入過程について解説する。詳し くは、ページボトムに記載の参考文献(北原・渡辺, 1972、北原, 1994や粉体工学会, 2010など)を参照されたい。<計算ソフト> 参考までに、式(Ⅰ-7)・式(Ⅰ-8)に各パラメーターの値を入力して実際に計算し、その結果を図示するExcelファイルを本サイトのサーバ ーに保存してあるので、目次-付録からダウンロードして試算されると理解が深まると思われる。具体的な粒子のHamaker定数は数多く 求められているので、文献(Bergdtrom, 1997や粉体工学会, 2010)を参照されたい。1.荷電粒子間の静電相互作用 水溶液中で、荷電粒子が互いに接近すると、両者の電気二重層に重なりが生じ(前記図Ⅰ-5・D)、重なり領域の対イオン個数濃度を増 加させる。この結果、表面荷電の静電気的反発作用に加えて、この領域の浸透圧Π[N/m2]が増加して自由エネルギー(= Πv [Nm=J]、 v:重なり領域の体積)が増大することとなる。 しかし、2つの粒径粒子の二重層の重なりによる自由エネルギーの増加量の計算はかなり複雑である。そこで、粒子径 a(100nm以上) が二重層の厚さκ(10nm前後)の10倍以上、すなわち、a≫1/κであれば、二重層の重なりを2枚の同符号に荷電した平行板に近似して扱 うことができる(電気回路で多用されるコンデンサーの極板は正負の対符号で帯電していることが大きな相違である)。多くの場合、こ の近似モデルでその概略を満足に説明できる結果が導かれる。 ここで、2枚の同サイズ・同符号に帯電の平行板の単位面積あたりに働くは力Pp[N/m2]は式(B-1)に示すように静電気力Peと浸透圧Po の和となり、PeとPoは、それぞれ式(B-2)および(B-3)で示される。 Pp = Pe + Po (B-1) Pe = -(ε/2) (dΨ/dx)2 (B-2) Po = (n+ + n–)kT – 2nkT (B-3) 一般に、Poは常にPeよりも大きく、さらに二重層の重なりによって表面電位Ψoに変化がなければ、Peを無視できる。この理由は、同 サイズで同符号に帯電した平行板であれば、それらの中間距離での面上では、その対称性から電界[V/m]はdΨ/dx = 0となり、Poのみを 考えればよいこととなる。1.1 荷電平行板の静電相互作用(Derjaguin近似) 式(B-1)(≒ 式(B-3))に式(A-1)を代入すると、平行板に働く単位面積あたりの力Pp(h)は、次式で表される。 Pp(h) = 2nkT{cosh[zeΨ(h/2)/(kT)] – 1} (B-4) h:2平行板間の距離[m]、Ψ(h/2):中間点における電位[V] 式(B-4)は複雑であるので、以下に示す近似を行う。 電位が低く、また電位の重なりが余り大きくない条件では、図B-2に示すように、式(A-6)で表される単独粒子の電気二重層の電位 Ψ(h/2)の2倍に相当するものと考えると、Ψp(h/2) = 2Ψ(h/2)、となる。 次に、zeΨ/4kT≪1の時には、解説(A)の式(A-7)の近似式にx = h/2を代入すると、次式が得られる。 Ψp(h/2) = 2Ψ(h/2) = 8kT/(ze)・γexp(-κh/2) (B-5) γ= tanh[zeΨo/(4kT)] (A-5) ここで、 式(B-4)の右辺のcosh項についてテイラー展開して3次項までの近似、cosh y ≒ 1 + (1/2)y2、を用い、この近似式に式(B-5) を代入すると、次式が得られる。 cosh[zeΨ(h/2)/(kT)] ≒ 1 + (1/2)[zeΨp(h/2)/(kT)]2 = 1 + 32γ2exp(-κh) 上式を式(B-4)に代入すると、次式で示される。 Pp(h) = 64nkTγ2 exp(-κh) (B-6) 以上のことから、同サイズの2枚の平衡した荷電平行板を遠距離∞からhまで接近させたときの単位面積あたりの必要エネルギー Vp[J/m2]は、式(B-6)を積分すると、次式で表される。 Vp(h) = -∫Pp(h)dh (h = ∞ → h) = (64nkTγ2/κ)exp(-κh) (B-7) 図B-2 同符号に荷電した2枚の平行板による電気二重層の重なり1.2 2粒子間にはたらく静電相互作用 粒子間の静電相互作用は、粒子半径 aとデバイ長の逆数κとの積κaの大きさによって基礎式もその近似解法も異なる。 図Ⅰ-5・Dに示すように、本モデルの条件(a≫1/κ)では電気二重層の厚さが小さいので、Deriaguin近似を導入して球を半径 aの薄い 円板と考えると、この2枚の円板間の静電相互作用力FR(h)は、次式で示される。 FR(h) = 2π{a2/(a+a)}Vp(h) = πaVp(h) (B-8) 式(B-7)を上式に代入して、h = ∞ → h の範囲で積分すると、静電相互作用によるVRエネルギーとして、次式が得られる。 VR(h) = 64πankTγ2/κ2 exp(-κh) (B-9) 式(B-10)についても同様に計算するか、または、PR(h) = – dVR(h)/dhからも求められる。 PR(h) = 64πankTγ2/κ exp(-κh) (B-10) 解説(A)の式(A-5)において、zeΨo/(4kT)≦1のとき、γ = tanh[zeΨo/(4kT)] ≒ zeΨo/(4kT)となり、この近似したγと式(Ⅰ-9)で示す κを上記の式(B-9)・(B-10)にそれぞれ代入すると、次の近似式が得られる。 PR(h) = 2πaεκΨo2 exp(-κh) (B-11) VR(h) = 2πaεΨo2 exp(-κh) (B-12)1.3 本モデル以外のコロイド系<厚い二重層または小粒子系:a<1/κ > このケースでは、Deriaguin近似が適用できず、Debye-Hueckel近似を適用した次の式が得られている。 VR(h) = 4πεΨo2a2/(h + 2a)・exp(-κh) (B-13)<広範囲のκaへ適用可能な式> Debye-Hueckel近似のもとで、粒子間のPoisson-Boltzmann方程式の近似解から得られた次式が提出されている。 VR(h) = 4πεΨo2a(h + a)/(h + 2a)・ln[1 + a/(h + a)・exp(-κh)] (B-14) 式(B-14)は、近距離 h≪aでは、a≫1/κの式(B-12)になる一方、遠距離 h≫aではa<1/κの式(B-13)に収束するので、広範囲のκaに適用 可能と考えられている。2.粒子間のvan der Waals相互作用 2つの原子間に働くLondon-van der Waal力は短距離力でそのポテンシャル力はその原子間距離の6乗に逆比例するので、遠距離におい てはその作用は働かない。しかし、コロイド分散系の各粒子には極めて多数の原子が含まれているので、これらの相互作用を加え合わせ ると、原子間に比べて粒子間引力は遠方にまで作用することとなる。 Hamker(1937)は、2枚の平行板および球形粒子間に働く引力のポテンシャルエネルギーVAを計算した。球形粒子間については、次 式で示した。 VA = – (A/6){2/(S2 – 4) + 2/S2 + ln(s2-4)/s2} (B-15) ここで、s = 2a + h、a:粒子半径[m]、h:粒子の最短表面間距離[m] である。a≫hの場合には、次式で近似される。 VA = – aA/(12h) (B-16) なお、2粒子間の引力PAは、式(A-16)を微分して次式で示される。 PA = aA/(12h2) (B-17) 解説(C) 粒子界面電荷の発生解説(D) 電解質効果とSchulze-Hardy法則図D-1 AgIの陽性ゾルにアルキル硫酸ナトリウムの添加濃度とζ-電位の関係測定値(Otterwill & Watanabe, 1960)を次式でフィッティングした。ζ = ζo tanh[(X – b)/a]、X = log xζo:120[mV]、x:添加濃度C[mol/L]、C10:a = 1.6;b = -3.2、C12:a = 1.0;b = -4.4、C14:a = 0.8;b = -4.8図D-2 AgIの陽性ゾルにアルキル硫酸ナトリウムの添加濃度と安定度比(W)の関係測定値(Otterwill & Watanabe, 1960)を次式でフィッティングした。Log W = c {cosh[a(X – b) – 1}、X = log xC10:a = 2.0;b = -3.2;c = 0.8、C12:a = 1.0;b = -4.2;c = 3.8、C14:a = 0.5;b = -4.8;c = 16表D-1 分散コロイドの臨界凝集濃度cfc [mmol/L]解説(E) 凝集速度解説(F) 表面張力と界面活性図F.1 表面張力のモデル実験図F.4 曲面における気相・液相の全圧(Pg、Pl )の違い液面:(a) 凹面(r>0)、(b) 凸面(r](https://static.wixstatic.com/media/a7b666_dc9e5c52e68d4403a20dd79ff6b1b723~mv2.jpg/v1/fill/w_397,h_302,al_c,q_80,enc_auto/%E5%9B%B3B-2%E3%80%80%E5%90%8C%E7%AC%A6%E5%8F%B7%E3%81%AB%E8%8D%B7%E9%9B%BB%E3%81%97%E3%81%9F2%E6%9E%9A%E3%81%AE%E5%B9%B3%E8%A1%8C%E6%9D%BF%E3%81%AB%E3%82%88%E3%82%8B%E9%9B%BB%E6%B0%97%E4%BA%8C%E9%87%8D%E5%B1%A4%E3%81%AE%E9%87%8D%E3%81%AA%E3%82%8A.jpg)
コロイドと界面現象<目次> はじめに Ⅰ.コロイドと界面現象 1.コロイドとは 2.疎水・親水コロイド 3.疎水コロイドの分散と凝集 4.親水コロイドの塩析 5.会合コロイドとミセル 6.コロイド溶液の物性 Ⅱ.解説 解説(A) 粒子界面の静電気現象 解説(B) 疎水性2粒子系の相互作用 解説(C) 粒子界面電荷の発生 解説(D) 電解質効果とSchulze-Hardy法則 解説(E) 凝集速度 解説(F) 表面張力と界面活性 解説(G) 界面活性剤の特性 解説(H) 吸着エネルギーと平衡式 解説(J) 高分子吸着と分散・凝集 付録:疎水コロイド相互作用の計算ソフト (ダウンロード) ※本ページは『水浄化フォーラム』より転載しています。<謝辞> 「水」の安全確保と環境保全に係る知識と技術を、「水の浄化」に関わる方への参考となるサイトとして『水浄化フォーラム』を執筆・編集・管理いただいている 環境技術学会 村上理事に心より感謝申し上げます。 はじめに コロイドおよびその現象は、生命を含む自然界において重要な役割を担い、人々の生活・産業においても様々な形で利用されている。水浄化の分野においても、コロイドの制御は主要な要素技術である。 水浄化において、原水中の濁質のうち、粒子径が10μm程度以上のものは単純な沈澱によって除去することが可能である。しかし、粒子径が1μm以下になると、コロイド粒子が懸濁状となり、ほとんど沈降せず、また急速ろ過では捕捉することもできない(図1)。さらに水中に溶解している有害な金属や非金属の原子・分子イオンを難溶性塩や水酸化物(共同沈殿を含む)として析出・沈降して分離除去するとき、1μm以下の微細な結晶性・不定形の粒子を生成するが、10μm程度以上の沈降性粗大粒子にまで成長できない例は少なくない。 わが国の水道における浄水処理において、一般的に、凝集・沈殿・急速砂ろ過を基本としたシステムが採用されている。この技術が微粒子の分離に優れ、安価・大量処理など多くの利点あるため、日本の近代水道が発祥して100年以上経過した現在でもなお主流技術として用いられている。また、種類の異なる様々な懸濁水(溶解性物質を不溶性物質へ変換する工程も含めて)は、建築・建設工事現場や生産・製造工程において発生し、凝集・沈殿分離は基本的な水浄化技術となっている。 以上の凝集工程の設計や維持管理(目次、関連ページ、参照)を適正に実施するためには、コロイドの性質とその分散・凝集の機構を理解することが大切となる。 図1 水浄化における汚濁物質のサイズとその分離・除去法本ページの目的と構成 本ページは、学校・大学の学生や企業での初心者を対象として、「水浄化におけるコロイドの凝集工程についての原理・操作」を理解するための基礎として、「Ⅰ.コロイドと界面現象」、および、「Ⅱ.解説」から構成されている。Ⅰ~Ⅱに記載の内容には、一部、重複したものも含まれている。重複した数式については、サブページを含めて本ページ全体を通して同一の式番号を記載している。文献・Web-Siteの引用 引用・参考にした文献は本ページボトムに示したが、引用した画像や動画はそれぞれのサイトをリンクしてあるので、それらのサイト内容も含めて理解されたい。 Ⅰ.コロイドと界面現象1.コロイドとは 1861年、スコットランドの化学者であるThomas Grahamは、水中でデンプンやタンパク質などの粒子が拡散する速度が遅いこと を発見し、これをコロイド(colloid)と名付けた。コロイド粒子(colloidal particle)とは、直径がおよそ1nm~1μm程度で、単一の 原子・分子サイズと比べて比較的大きな粒子で、媒体中に分散した状態で存在する。 1.1 身近なコロイドの事例 コロイドとは、コロイド粒子(固体や液滴)が他媒体(気体・液体・個体)に分散した系全体のことを指す。身近な例でいえば、牛 乳や泥水などがコロイドである。牛乳のような分散質が液体コロイドの溶液は一般的にエマルション(emulsion)といい、これに対し て、泥水のような分散質が固体コロイドの溶液は一般的にサスペンション(懸濁、suspension)という。 コロイドの分散媒は、液体または固体の場合が多いが、分散媒が気体の場合もあり、そのようなコロイドはエアロゾル(aerosol)と いう。 ゾル(sol)とは流動性を持ったコロイドのことで、これに対して、加熱や冷却などの何らかの原因で、ゾルが流動性を失ったものをゲ ル(gel)という。身近なゲルの例としては、寒天・ゼリー・豆腐などがある。 表Ⅰ-1 身近なコロイドの分類と実例1.2 コロイドの分類 コロイドは、その構造により、① 高分子コロイド(polymer colloid)、② 会合コロイド(association colloid)および ③ 分散コロイ ド(dispersed colloid)に分類される。 高分子コロイドは、分散媒に分散した分子1個の大きさがコロイドサイズの分散系である。コロイド化学の初期には、高分子コロイド の研究がコロイドの主流であった。コロイド研究の先駆者であったThomas Grahamが最初に示したコロイドは、いずれも天然高分 子であった。現在では、高分子化学(polymer chemistry)という別の学問分野ができ上がっているので、高分子をコロイド化学で扱 うことは、少なくなった。 会合コロイドは、多くの分子が集まって、コロイドの大きさを持つようになった分散系を示す。洗剤などの界面活性剤分子は、溶液 中である濃度以上になると、ミセル(micelle)と呼ばれるコロイドサイズの会合体を形成する。 分散コロイドは、溶媒には本来溶解しない不溶性物質の分散系である。溶解するはずのない物質が媒体中で分散しているのだから、 分散コロイドは熱力学的には不安定な系であり、条件によって破壊することができる。表Ⅰ-1で示したコロイドはすべて分散コロイ ドであり、分散コロイドは最も身近に溢れているコロイドである。 表Ⅰ-2 コロイドの種類1.3 コロイドの形状と観察(1) 大きさ コロイド粒子の大きさは直径が1nm~1μmの範囲で、ろ紙を通過するが半透膜を通過しない程度の大きさである。この性質を使 用して分子とコロイド粒子を分けることができる。図Ⅰ-1 コロイド粒子の大きさとその分離(2) 形状 コロイド粒子の形状には、球状、棒状、針状、板状、繊維状、膜状のものなど、コロイド系の物質・分散媒やその生成過程を含め て物理・化学的条件により様々な形状で存在している。図Ⅰ-2 コロイド粒子の形状モデル(3) 観察 コロイド粒子は、光学顕微鏡では小さすぎて観察することができないが、限外顕微鏡や透過型電子顕微鏡(TEM)などを使えば、 コロイド粒子を観察することができる。限外顕微鏡では、特殊な照明装置により微粒子の散乱光(チンダル光)を観察して、微粒子 の動きを見ることができる。また、透過型電子顕微鏡では、可視光の代わりに電子線を照射して、対象を観察することができる。 コロイド粒子は非常に小さいので、これを観察するには特殊な装置が必要となる。 2.疎水・親水のコロイド 2.1 コロイド状態の保持 分散コロイドは、不溶性物質の粒子が媒体中に分散している系のことであって、溶解性物質の溶液とは明確に区別される。溶液は結 晶がその物質の構成単位である原子や分子のレベルまで解離して溶媒に溶けている状態であるのに対して、コロイドは多数の原子・ 分子が集まって1つの粒子(例えば、不溶性の金属酸化物では、1nm粒子でおよそ数百個、1μmでおよそ数×1011個の金属と酸素の 原子から構成される粒子)となり、それらが媒体に分散している状態である。単一分子サイズが大きい高分子コロイドなどの例外も あるが、コロイドは、一般的には「多数の原子・分子から構成される集合体が分散媒に分散している系」である。したがって、コロ イドとして分散状態を保つためには、いくつかの条件が必要となる。 (ⅰ)コロイド粒子がさらに小さな粒子(原子や分子)にまで解離されないこと 例えば、結晶・粉末状の食塩NaClやショ糖C12H22O11は、水中ではNa+・Cl–イオンやショ糖C12H22O11の単分子にまで 解離・溶解しているので、コロイドとはいえない。食塩やショ糖は、水中では結晶・粉末状の状態よりも、解離して水和したイ オン・分子での状態の自由エネルギーが低く、熱力学的に安定であるからである。 (ⅱ)コロイド粒子同士が衝突・凝集し、さらに大きな粗粒子にならないこと 分散コロイドは熱力学的には不安定な系で、コロイド粒子は安定になろうと凝集してより大きな粒子になろうとする作用が働 く。コロイド粒子が凝集して大きな粒子になると、単に浮上するか沈降するかという状態となり、コロイドではなくなってしま う。 分散したコロイド粒子が凝集しないようにするには、主に以下の2つの方法がある。 第一の方法は、コロイド粒子の表面を帯電させることである。例えば、後述する図Ⅰ-5に示すように、コロイド粒子の表面を「正」 に帯電させたとする。このとき、電気的に中性を保とうとして、表面電荷量と同量の負イオンが過剰にコロイド粒子を取り巻いてい る。粒子の表面電荷と反対符号のイオンを対イオン(counter ion)といい、このような状態を電気二重層(electric double layer)が できているという。なお、多数の対イオンは粒子表面の電荷に引かれて統計的に分布しているものの、個々のイオンは自由に液中を 拡散して遠くまで動くことができる。 ところで、ブラウン運動により2つの粒子が接近し、相互の電気二重層が重なるようになると、図Ⅰ-3に示すように、重複した二重 層領域の浸透圧 [= Π(h):h は粒子表面間の距離] の増加による反発力 Po(h)が働き、自由エネルギー [= ∫ Π(h)v(h)dh:h = ∞→h で積分; v(h)は重なり領域の体積] が増大することによって熱力学的に不安定となり、粒子同士の合体を妨げるようになる。 基本的には気体の圧縮に必要な力とそれに要する仕事エネルギーの関係と同じようなものと考えると理解しやすい。ただし、重なり 領域内でのイオン濃度分布が均一でないので、計算は複雑となる。 図Ⅰ-3 電気二重層の重なりによる浸透圧の増加と粒子間反発力の発生 分散コロイドが凝集しないための第二の方法は、図Ⅰ-4に示すように、コロイド粒子の全表面を溶媒分子で覆っておくことであ る。コロイド粒子が互いに接近しても、表面を覆っている溶媒分子が離れなければ、コロイド粒子間の接触を妨げることができ る。図Ⅰ-4 表面が水素結合による水分子層で覆われている親水性粒子同士の接近 2.2 疎水性コロイド コロイド粒子のうち、主に上記の第一の方法のみで水中で分散している場合、これを疎水コロイド(hydrophobic colloid)という。 水に対して不溶であり、本来沈降すべき物質がコロイド粒子のサイズになった上に、何らかの理由(詳しくは、Ⅱ.解説(C)を参 照)で表面が帯電してしまったために、粒子間に反発力が働き、合体・集合できなくて微細な状態のコロイド粒子が分散状態になっ ている。一般的に、疎水コロイドは、その大半が無機物質である。 2.3 親水性コロイド 上記の第二の方法が主たる理由で水中に分散している場合には、これを親水コロイド(hydrophilic colloid)という。コロイド表面に 溶媒である水分子層が付着して離れないのは、水に対して親和性が高いからである。親水コロイドには分子コロイドや会合コロイド が多く、その大半が有機物質である。 表Ⅰ-3 コロイドの分類と特徴3.疎水コロイドの分散と凝集 3.1 DLVO理論による分散・凝集機構 疎水コロイドは一般的に不安定な系で、粒子表面の電荷密度や溶液の電解質濃度を変化にさせると、分散したり、凝集したりする。 この分散・凝集のメカニズムを以下に説明する(各式の誘導はⅡ.解説(B)を参照)。 疎水コロイドの分散・凝集の現象については、粒子の荷電表面による電気二重層による反発力作用および粒子内の構成原子・分子間 のvan der Waals引力作用の相反する作用によって理論的に説明することができ、これをDLVO理論という。「DLVO」とは、旧ソ 連の化学者であるDerjaguinとLandau、オランダの化学者であるVerweyとOverbeekの4人の研究者の頭文字に由来している。 (1) 拡散電気二重層 図Ⅰ-5・Aに示すように、電解質溶液中に分散している荷電粒子の界面近傍の溶液側は拡散電気二重層が形成される。この二重 層は、次の相反する2つの作用によって説明される。以下、z-z型対称電解質の溶液とする。 (1) 静電気力によって界面電荷(例えば、正の電荷)に対して、反対符号のイオン(対イオン)は界面へ近づくように引力が 働き、同符号のイオン(同イオン)は遠ざかるように斥力が働くので、図Ⅰ-5・Cに示すように界面近傍では対イオン個 数(n–)と同イオン個数(n+)との濃度差Δn(= n+ – n–; < 0)が生じる。 (2) 一方で、液中では正負の両イオンは熱運動による拡散力がそれらの濃度差Δnを減少させるように働く。 粒子界面から遠ざかるにつれて静電気力が減衰するのに対し、拡散力は一定であるので、遠く離れたところでは、拡散力 が支配的となり正負イオンの個数濃度は等しくなる(n+ → n∞、n– → n∞、Δn → 0;n∞は母液中の正負のイオン 数)。 (2) 電気・拡散二重層を示す基本式 正負の符号が異なるイオン個数が異なると、溶液系のある無限小の体積Δv[m3]が電荷を有するようになり、その密度ρ[C/m3] は次式で示される。 ρ = zeΔn/Δv (Ⅰ-1) また、拡散層における電荷ρと電位Ψの関係は、次のPoissonの式で示される。 ∇2Ψ = – ρ/ε (Ⅰ-2) ただし、ε = εrεo、ε:溶媒の誘電率、εs:溶媒の比誘電率、εo:真空の誘電率 式(Ⅰ-1)と式(Ⅰ-2)の関係より、界面電位Ψoとする球形の粒子表面の法線方向をx軸とし、界面からの距離 x[nm]における電位 は、次式で近似される。 Ψ(x) = Ψoexp(-κx) (Ⅰ-3) ここで、κ は式(Ⅰ-9)で示される。 Ψ(x)の分布は、図Ⅰ-5・Bに示すような二重層電位Ψの減衰として表すことができる。 なお、界面電位Ψoは一般に測定困難な量であって、測定可能な「すべり面」における電位(ζ-電位)で近似することが多い。す べり面とは、粒子と液とが相対的に動くときの境界面である。 図Ⅰ-5 荷電粒子の電気二重層と2粒子の接近のモデル図A:電気二重層のモデル、B:固液界面からの距離と電位、C:固液界面からの距離とイオン個数の濃度、D:粒子同士が接近したときの電気二重層の重なり 留意事項 吸着性イオン(界面活性剤イオン、高分子イオン、高原子価イオン、錯イオンなど)が存在すると、その濃度に応じた吸着が起 こる。吸着イオンの大きさに相当する厚さの吸着層が形成され、その吸着層と溶液との界面に電位(Stern電位Ψδという)が 発生する。対イオンはその外側に分布するので、Ψの変化はΨoではなくて、Ψδから出発する(Ⅱ.解説(B)-図B-1(C)を参 照)。本章では、吸着性イオンが共存しないコロイド系について議論を行う。 (3) 接近2粒子間に働く力とその系の自由エネルギー 図Ⅰ-5・Dに示すように、球状で半径 aの2つの荷電粒子が接近して、それらの表面の最短距離(2粒子の中心を結ぶ直線とそ れらの粒子表面との交点間の距離)をhとする。 粒子同士が接近したとき、斥力PR[N](>0)および引力PA[N](<0)の相反する力が働き(添字、R: repulsion、 A:aggregation)、これらの合力は次式で示される。合力P<0であれば、粒子はより接近するように凝集力が働く。合力P >0であれば、粒子は遠ざかるように分散力が働く。 P(h) = PR(h) + PA(h) (Ⅰ-4) 斥力 PRの原因は、疎水コロイドの分散している溶液で、電気二重層を持つ2つのコロイド粒子が接近すると、図Ⅰ-3に示した ように電気二重層内の対イオンの重なりにより浸透圧が増大するので、コロイド粒子には反発力が働くからである。 一方で、引力 PAの原因は、コロイド粒子同士がかなり近くまで接近したときには、粒子間にvan der Waals力に起因する粒 子間引力が働くからである。 しかし、その粒子系において、「凝集するか、分散するか」は、その系が自由エネルギー的に「安定であるか、不安定である か」によって決まる。コロイド2粒子系における自由エネルギーVは、斥力および引力に起因するエネルギーVRおよびVAの和 として、次式で示される。 V(h) = VR(h) + VA(h) (Ⅰ-5) 2粒子間に働く合力P(h)とその系の自由エネルギーには次の関係がある。 dV(h)/dh = P(h) または V(h) = ∫|P(h)|dh (h = ∞ → h) (Ⅰ-6) ただし、V(∞) = 0 ここで、Ⅱ.解説(B)で詳述する電気二重層モデルの条件下では、半径 a[m]の2個の荷電粒子が、遠くから粒子界面距離 h[m] に接近したときの合力P(h)および自由エネルギーV(h)は、次式で近似的に示される。 P(h) = 2πaεκΨo2 exp(-κh) – aA/(12h2) (Ⅰ-7) V(h) = 2πaεΨo2 exp(-κh) – aA/(12h) (Ⅰ-8) κ2 = 2nz2e2/(εkT) (Ⅰ-9) κ = 3.3×109z√C [/m] (at T = 298K) (Ⅰ-10) なお、式(Ⅰ-7)~式(Ⅰ-10)において、Ψo:粒子-水界面における電位[V]、ε:水の誘電率(7.08×10-10[N/m2/C2]、 25℃)、A:Hamaker定数、z:z-z型対称電解質の価数、n(= n∞ = 1.0×103C):単位体積中の電解質イオン個数 [1/m3]、C:電解質濃度[mol/L]である。 (4) 疎水コロイドの凝集と分散 一般に系の自由エネルギーVの値が低いほど、その状態はより安定となる。2つの荷電粒子が接近したときの表面間距離 hに対す る自由エネルギーV(h)と粒子間に働く合力P(h)の関係の事例を図Ⅰ-6に示す。 一般に、V(h)の極大値Vmax(dV(h)/dh = P(h) = 0 → PR = PA)が存在し、凝集系と分散系の境界にエネルギー障壁が現れ る。粒子が接近したとき、「分散 → 凝集」へ移行するには、このエネルギー障壁を越える活性化エネルギーが必要となる。コロ イド粒子はブラウン運動をしており、そのエネルギーはkT(= 26meV、25℃)を用いて議論される。Durhanによれば、半径 100nm以上の粒子について、Vmax>15kTでは、ブラウン運動によってこの障壁を越える確率が極めて低く、長期間にわたっ てコロイド状態は安定に存在する。Vmax<15kTでは、この障壁を越える確率が高くなりコロイド系は不安定となり緩速凝集が 進行し、さらにVmaxが消失すると急速凝集が起こることとなる。 留意事項 本章での説明はコロイド状態の安定性をエネルギー的に論じているが、その状態が時間的にどの程度維持できるかについては、 別の問題である。コロイドの凝集速度については、Ⅱ.解説(E)を参照されたい。 図Ⅰ-6 球形・同サイズ・同荷電の2粒子系に働く力と自由エネルギーP:粒子間に働く合力、PR:静電気的反発力、PA:van der Waals引力、V:2粒子系の自由エネルギー{ただし、V(∞) = 0 とする}、VR:静電気的エネルギー、VA:van der Waalsエネルギー、a:粒子半径、h:2粒子表面の最短距離、Ψo:表面電位(Stern電位)、A:Hamaker定数、1/κ:二重層の厚さ(Debye長さ) 具体的計算:図Ⅰ-6については、Excelファイルをダウンロードし、具体的に試算するとよい。なお、ページトップの目次-付 録に記載のファイルも同じものである。 学生や初心者の方は、同ファイルの各パラメータに具体的な数値を記入して、Vmaxは「どの因子によって大きく影響される」 か実感されたい。そして、「その因子が変化する原因はどのような理由によるもの」か考察することが、現実の水浄化プロセス の開発・改善や維持管理において役立つこととなろう。 3.2 コロイドの分散・凝集の因子 コロイド粒子が長時間にわたって安定であるか、凝集するかは、コロイド系の自由エネルギーの極大値Vmaxの高さに依存すること を前節で述べた。ここでは、Vmaxの高さに及ぼす主な因子について述べる。Vmax (= V(ho))においては、P(ho) = 0であるので、 式(Ⅰ-7)および式(Ⅰ-8)より、次式が得られる。 Vmax = 2πaεΨo exp(-κho) (1 – κho) (Ⅰ-11) 上式と式(Ⅰ-10)から、a = 一定、T = 一定のとき、Vmaxは、粒子界面の電位Ψoおよび電解質の電荷 zとその濃度Cに大きく依存す ることが分かる。 (1) 粒子表面電位 Ψoとエネルギー障壁 Vmaxの高さ 界面電位Ψoを変化したときの、各Ψo値に対する自由エネルギーV(h)と距離 hの関係を図Ⅰ-7に示す。表面電荷が高くなると、 Vmaxは高くなる。 Ψo<15mVでは Vmax<10kTとなり、ブラウン運動エネルギーによってエネルギー障壁を越える確率が高くなり、分散系は不 安定で凝集が起こることが推定される。逆に、Ψo>25mVでは Vmax>40kTとなり、分散→凝集への活性化エネルギーが高 く、凝集速度は極めて遅くなり分散系は安定であることが推定される。 図Ⅰ-7 球形・同サイズ・同荷電の2粒子系の自由エネルギーに対する表面電位の効果記号等の説明および計算については、図Ⅰ-6と同じ。 (2) 酸化物/水酸化物の表面の等電点 酸化物/水酸化物の固体粒子を水に分散させると、その表面は水和して、次の化学平衡を起こす。 -O-M=O(粒子表面)+ H2O → -(OH)-M-OH -M-OH + H+ ⇄ -M-OH2+ (低pH) -M-OH + OH– ⇄ -M-O– + H2O (高pH) 低pHでは水素イオンH+と、高pHでは水酸化物イオンOH–と粒子表面-M-OHとの平衡反応(不可逆的な化学吸着ではない) が生じ、正または負に帯電する。表面電荷が消失するpHoが高・低pHの中間で存在し、このpHo値を等電点(iso-electric point, iep)という。任意のpHにおける表面電位Ψoはネルンストの式から、次式で示される。 Ψo = -ne(pH – pHo)/(kT) (Ⅰ-12) = – 59(pH – pHo) [mV] (at 25℃) 以上のことから、酸化物/水酸化物粒子の分散・凝集はpHに大きく依存することとなり、凝集操作においてpHは正確に調整す る必要がある。表Ⅰ-4に、酸化物/水酸化物の表面の等電点を示すpHoを示す。 表Ⅰ-4 酸化物/水酸化物の表面の等電点sp:流動電位法、eo:電気浸透法、mep:電気泳動法文献(古澤, 2004)のデータをpHo値(測定方法によって、同じ物質でも値が異なるが)の順に並び替えた。訂正:γ-Al2O4 → γ-Al2O3 (3) 電解質添加によるエネルギー障壁の低下 前節で述べたように酸化物粒子などではpH調整により表面電荷を制御できるが、現実には溶液のpHを特定値に保つ必要もあ る。また、コロイド粒子間に働く van der Waals力の大きさは、コロイドを構成する内部の原子・分子に固有のもので粒子表 面の性状に無関係であるので、溶液(分散媒)の条件によって変えることができない。 一方で、先に示した図Ⅰ-5・Dから分かるように、粒子・溶液界面の電気二重層が厚いほど、粒子同士が接近したときの重なり 領域が広くなり、コロイド粒子間に働く反発力が増加する。 そこで、疎水コロイドが分散している溶液に電解質を加えると、上式(Ⅰ-10)で示したように、その濃度が高いほど、電気二重層 の厚さ(1/κ)は小さくなり、粒子間の反発力は減少する。さらに添加する電解質イオンの価数zが大きくなると、その効果は格 段に高くなる。 図Ⅰ-8に塩化ナトリムの添加によるエネルギー障壁Vmaxへの効果を示す。この事例では、NaCl濃度>100mmolでは、エネル ギー障壁Vmax<15kTであるので、コロイド系は不安定となり、粒子の凝集が進行することが推定される。 なお、凝集に必要な電解質の濃度は、解離イオン価数zの6乗に反比例し、多価電解質の凝集効果が極めて効果的であることが実 験により分かっているが、理論的にも説明できる(Ⅱ.解説(D)を参照)。 図Ⅰ-8 球形・同サイズ・同荷電の2粒子系の自由エネルギーに対する電解質の添加効果記号等の説明および計算については、図Ⅰ-6と同じ。4.親水コロイドの塩析 親水コロイドのコロイド粒子表面には、親水性の官能基(-OHや-COOH、-CO-、-NH2など)を多数有している。上記図Ⅰ-4 に示したように、これらの親水基が水素結合によって水分子を粒子表面に強く引き付けているために、水和水層が立体障害になって コロイド粒子同士の凝集は妨げられている。したがって、親水コロイドを凝集させるためには、表面での水素結合を切り、コロイド 粒子を覆っている水和水を表面から剥ぎ取らなければならない。 電解質をコロイド溶液に加えると、水中でイオンに電離する。これらの電離イオンは、親水基よりも強く水分子と引き合うので、親 水コロイドに塩化ナトリウム NaClなどの塩を加えれば、理論上は水和水を失って、親水コロイドは沈殿するはずである。しかし、 NaCl濃度を1mol/Lぐらいにしても、なかなかコロイド粒子は沈殿しない。水溶液には約1000/18 ≒ 56mol/Lの水分子が存在為て いるのに対して、塩濃度が1mol/L程度ではイオンの数が少なすぎて、親水基と水分子の水素結合を切るに至らない。親水コロイドに ついては、少量の塩を加えただけでは凝集が起こらず、NaCl濃度が5~10mol/Lぐらいになって、初めて親水基と水分子の水素結合 が切れ、親水コロイドの凝集が起こる。このように親水コロイドに多量の電解質を加えて凝集させることを、一般的に塩析(salting out)という。 セッケンのコロイド溶液に飽和食塩水を加えてセッケンを析出させたり、タンパク質のコロイド溶液である豆乳にニガリMgCl2や硫 酸カルシウムCaSO4を加えて豆腐を作るのは、塩析を利用したものである。 (1) 保護コロイド 疎水コロイドに親水コロイドを加えると、疎水コロイドが凝析しにくくなることがある。このときに加える親水コロイドを保護コロ イド(protective colloid)という。 これは、疎水コロイドの周りを親水性の保護コロイドが取り囲み、さらにその周りを水分子が水和しているため、疎水コロイドの表 面が親水化されるからである。保護コロイドを加えると、疎水コロイドは電解質に対して安定になる。例えば、疎水性である赤色ア ルカリ性金コロイドに対して、ゼラチンは強い保護作用を示す。その他の例としては、墨汁のニカワやマヨネーズの卵黄は、代表的 な保護コロイドである。ただし、この保護作用の強さは物質の種類だけでなく、pHや調整法などにより著しい影響を受ける。 5.会合コロイドとミセル 界面活性剤は、生活・産業において広く活用されている。水浄化においても、懸濁水の凝集剤として利用されている。詳しくは Ⅱ.解説(G)に記載しているが、ここではその代表的な性質を概説する。 5.1 界面活性剤とミセル ミセル(micelle)とは、界面活性剤の分子またはイオンの集合体のことである。界面活性剤は、分子内に親水基と疎水基の両方を持つ ため、両親媒性分子とも呼ばれる。次の図Ⅰ-9に代表的な界面活性剤であるステアリン酸ナトリウムC17H35COONaの構造式を示 す。 図Ⅰ-9 ステアリン酸ナトリウムC17H35COONaの構造式と略号 水溶液中の界面活性剤の濃度を上げていくと、水溶液中で界面活性剤が集合して、大きなミセルを形成する。少量の界面活性剤を添 加した水溶液中では、ミセルは形成されない。 界面活性剤分子は分子内に疎水基があるため、水中では不安定である。水はその分子間の凝集力が大きいため、疎水基を水からはじ き出そうとする傾向がある。図Ⅰ-10・Aのように、少量添加した界面活性剤の大半は、空気-水界面へ移動し疎水基を空気側へ向け て配置される。また、水と油のような状況でも、界面活性剤はその界面へと移動・配置される。界面活性剤の界面吸着能はその重要 な物性の1つである。界面活性剤がミセルを形成し始める濃度を臨界ミセル濃度(critical micellar concentration、cmc)といい、 この濃度は、コロイドであるかないかを区別する重要な値である。 水溶液中の界面活性剤の濃度を上げていき、cmcに達すると、それ以上は界面に存在できない状態となる。この状態は、溶液の表面 全体が界面活性剤分子で覆われ、図Ⅰ-10・Bのように、表面配置が飽和してしまった状態である。さらに濃度上げていくと、行き場 のなくなった界面活性剤は分子同士で疎水基を重ね合わせ、親水基を外側(水側)に向けて互いに集まることにより、図Ⅰ-10・Cのよ うに安定な集合体を形成して水中に分散する。この集合体がミセルである。 図Ⅰ-9 ステアリン酸ナトリウムC17H35COONaの構造式と略号 このミセルの大きさと形状は、直径が分子の長さの約2倍程度の球状粒子であり、コロイドの範囲に入る。したがって、界面活性剤の 濃度がcmc以上になって初めて、界面活性剤の水溶液はコロイドになることができる。界面活性剤の水溶液は、cmc以下の濃度では コロイドにはならないので、濃度によってコロイドになったり、そうでなくなったりする興味深い性質を持つ。濃度をcmc以上にす れば、このミセルは自然と生成する。 5.2 不溶性物質の可溶化 界面活性剤を使うと、水と油のように互いに混ざり合わない物質の一方を、他方に分散させることもできる。これは、界面活性剤が ミセルを形成して、ミセル内にその物質が取り込まれるからである。図Ⅰ-11・Aは、ミセル内に油相が取り込まれ、水中に油が分散 している事例である。液体に溶けにくい物質が界面活性剤の存在下でその液体に溶けるようになる現象を可溶化(solubilization)とい う。 界面活性剤溶液への可溶化は、臨界ミセル濃度以上で起こる。この場合の可溶化量と界面活性剤の濃度との間には、一般的に図 Ⅰ-11・Bのような関係がある。このグラフから、逆に臨界ミセル濃度を間接的に求めることもできる。 図Ⅰ-11 界面活性剤の添加による油性物質の水中への可溶化A:O/Wマイクロエマルジョンのモデル(●:油の粒子)、B:界面活性剤の濃度と油の可溶化量 ミセルには、水相(W)に油相(O)が分散するO/Wエマルジョンと、油相に水相が分散するW/Oエマルジョンがある。O/Wの代表例は 食器に付着した油の可溶化で、W/Oの代表例は油井原油中に含まれる水分である。 可溶化量が増すと、ミセルは膨らんでいく。光の散乱状態は、ミセルが膨らむと増大し、液は半透明になって乳光を発したり、やや 濁って見えたりする。そこで、この現象を界面活性剤の乳化作用(emulsifying action)という。マヨネーズや乳液などには界面活性 剤が使われており、この乳化作用のために、白く濁って見える。 前述した水-油-界面活性剤の3成分系であるが、この系に中級アルコール(炭素数4~8)を補助剤として添加し4成分系にすると、図 Ⅰ-12に示すように、水に対して多量の油を(O/W)、または、油に対して多量の水(W/O)を含む広い組成範囲のエマルジョンを つくることができる。 図Ⅰ-12 オクチル硫酸ナトリム-ヘキサノール-デカン-食塩水の4成分系でのマイクロエマルジョン(ME)の生成6.コロイド溶液の物性 6.1 透析 コロイド粒子は、ろ紙の穴より小さいので、ろ紙を素通りして分離できない。しかし、セロハン膜やコロジオン膜の穴よりは大きい ので、これらの半透膜を通過できない。一方で、コロイド粒子より小さなイオンや分子は、このセロハン膜の穴をも通ることができ る。そこで、このような装置を使うことで、小さなイオンや分子を除き、コロイド粒子のみの溶液にすることが可能となる。この操 作を透析(dialysis)という。 透析を利用した水酸化鉄(III)・Fe(OH)3のコロイド溶液の作成を説明する。沸騰水に塩化鉄(III)・FeCl3水溶液を加えると、加水分解 反応が起こり、赤褐色のFe(OH)3のコロイド溶液が作成できる。沸騰水での反応の理由は、高温のために加水分解反応が急激に進む ので、多数に生成したFe(OH)3の小さな結晶核が大きな沈殿粒子まで成長できず、コロイド粒子のサイズで成長が停止しているから である。このコロイドは、溶液中の水素イオン・H+または鉄(III)イオン・Fe3+が表面に吸着しているので、正に帯電した疎水コロイ ドとなっている。 FeCl3 + 3H2O → Fe(OH)3↓ + 3HCl 生じたコロイド溶液を半透膜であるセロハン袋に入れて、流水中に浸して透析を行うと、水素イオン・H+や塩化物イオン・Cl–は拡 散によりセロハン膜を通過して流出していく。しかし、Fe(OH)3のコロイド粒子は半透膜を通過できず、セロハン膜内に留まる。こ の操作によって、Fe(OH)3のコロイドをセロハン袋中に精製することができる。 写真Ⅰ-1 (左)赤褐色の水酸化鉄(III) ・Fe(OH)3コロイド溶液、(右)セロハン膜による水酸化鉄(III)の精製 血液透析 透析を有効に利用しているのが、私たちの体の中にある腎臓である。腎臓には、血液中に含まれる尿素(NH2)2COなどの老廃 物を取り除く働きがある。腎臓病により、腎臓の機能が低下してくると、老廃物を体外に排泄できなくなり、尿毒症により生命 の危機に陥ることとなる。これを回避するために、人工透析が行われる。人工透析には、図Ⅰ-13に示すような血漿分離器が用 いられている。 まず、体外に取り出した血液を血漿分離器に通して、血球成分と血漿成分に分離する。赤血球や白血球などの血球成分は透析膜 を通過できないが、小さい分子である尿素(NH2)2COは透析膜を通過するので、これらを分離することができる。このとき分 離された血漿の代わりに、新鮮な血漿もしくはアルブミン溶液を補充する。 人工透析は、半透膜としての作用が弱った腎臓の働きを、このようにして人工的に行う治療法である。 図Ⅰ-13 血液透析の原理 6.2 光学的性質 コロイドは必ずしも濁っているとは限らず、透明または半透明なものも多い。しかし、透明に見えていても、コロイドの横から強い 光を当てると、光の通路が光って見える。これは、コロイド粒子の大きさが可視光の波長(350~700nm)とほぼ等しいため、その 表面で光がよく散乱されるからである。この現象をチンダル(Tyndall)現象といい、この光をチンダル(Tyndall)光という。これ はコロイドの特性の1つであり、チンダル現象の有無により、コロイドを見分けることが可能となる。 着色物質は光を吸収する。吸収の極大波長は分子・イオン・結晶では、物質に固有なもので、それぞれ固有な色を呈している。しか し、コロイドの色は物質に固有なものではない。 光の散乱と吸収の度合いを一つにまとめると、 ln Io/I = (ε+τ)・l ここで、Io/I は入射光/透過光の強さ、l は測定セルの厚さ、ε/τ は吸収係数/濁度である。ε = 0 のときにThydall式、τ = 0 のと きにLambert式となる。測定セル中のコロイド粒子数をN、粒子半径をaとすると、 ε = πNa2QA τ = πNa2QS (Ⅰ-13) となる。QA/QSは吸収因子/散乱因子といわれ、粒子半径 a、測定波長λ、屈曲率などの関数である。 粒子による散乱には、レイリー(Rayleigh)散乱とミー(Mie)散乱がある。レイリー散乱は、光の波長よりも小さいサイズの粒子 による散乱現象である。ミー散乱は、光の波長程度のサイズの粒子による散乱現象である。粒子のサイズが大きくなるとミー散乱と 幾何光学の双方の手法による計算結果が類似するようになる。 散乱波の波長λと散乱粒子の直径 d(= 2a)に関するサイズパラメータとして、 α = πd/λ があり、α≪1 はレイリー散乱、α~1 はミー散乱、α≫1 は幾何光学近似で表現できる。 写真Ⅰ-2 チンダル現象の事例 上式で示したように、チンダル現象は光の散乱が原因で、原子やイオンのような小さな粒子では光を散乱しないが、コロイドぐらい の大きさの粒子では光をかなり強く散乱する。なお、疎水コロイドのチンダル現象は比較的はっきり現れるが、親水コロイドのチン ダル現象はあまりはっきり現れない。 チンダル現象は、主にミー散乱によるものが大きい。レイリー散乱は、光の波長の依存性が高く、波長の短い青色の光は、赤色の光 よりも強く散乱される。長い波長の光は粒子による散乱が少なく、波長の短い光ほど粒子にょる散乱が起きやすい性質がある。空が 青いのは、レイリー散乱より説明できる。これは、大気中の微粒子により、青色の光が強く散乱されるからである。また、ミー散乱 は、波長の依存性が低いので、どの波長の光も同程度に散乱する。雲が白く見えるのは、ミー散乱が原因である。 表Ⅰ-5 ミー散乱とレイリー散乱の違い 6.3 微粒子の運動 微粒子は、その密度が媒質のそれよりも大きい場合、重力による下降運動するとともに、熱運動としてのブラウン運動も行ってい る。この両運動の兼ね合いで、粒子全体としての運動が決まる。 (1) 沈降 重力 Fgで下降する場合には、媒質から抵抗 Ffを受ける。上下方向の流れがない媒質中では、FgとFfがつり合うと粒子は等速 uで下 降し、これを沈降という。 粒子の半径 aの球とすると、浮力を補正した重力は、 Fg = (4/3)πa3(ρ – ρo)g (1) ρ・ρo:粒子・媒質の密度、g:重力加速度 抵抗力は媒質の摩擦抵抗で、摩擦抵抗をf、下降速度を uとすると、 Ff = f・u (2) 球状粒子は剛体でその濃度が希薄な場合(自由沈降)には、媒質の粘度をηとすると、 f = 6πηa (3) Fg = Ffの場合には、上記3式の関係より、下降速度 uは次式で示される。これをStokesの式という。 u = 2a2(ρ – ρo)g/(9η) (Ⅰ-14) なお、高速回転で遠心力を利用する場合には、重力加速度 g → 遠心力の加速度 ω2x(ω:角速度、x:回転中心から粒子までの距 離)を用いる。この方法は小さい粒子の沈降・分離に用いられる。 (2) ブラウン運動 イギリスの植物学者であるRobert Brownは、1827年に植物の花粉から生じた微粒子が、不規則な運動をすることを発見した。し かし、発見当時、この現象は「花粉の生命力に基づくものである」と誤解されていた。Brownは、これをブラウン運動(Brownian motion)と名付けた。その後、他の微細な粒子でも、同様の現象が起こることが確認されたが、長い間その原因は不明のままであっ た。 1905年に相対性理論で有名なAlbert Einsteinが、ブラウン運動の原因を突き止めた。Einsteinは、熱運動する媒質分子の不規則な 衝突により、ブラウン運動が引き起こされるということを、統計力学を駆使して理論的に説明した。媒質に浮かぶ微粒子は、各瞬間 毎に非常に多くの媒質分子に衝突されているが、その衝突はデタラメに起こるので、ある瞬間に微粒子が受け取る運動量はつり合っ ていない。この衝突の不均衡のために、粒子が動くのである。 ブラウン運動は粒子の不規則な熱運動であるから、統計的に計算できる。時間 tで z軸方向へ動く距離の平均 は、次式となる。 <x> = (2Dt)1/2 (1) ここで、D は粒子の拡散係数である。これをEinsteinのブラウン運動という。さらに、Einsteinによると、 D = kT/f (2) f は摩擦係数で、前節<沈降>の式(3)を用いて、次に示すEinstein-Stakesの式が得られる。 D = kT/(6πηa) (Ⅰ-15) これを式(1)に代入すると、 <x> = [kTt/(3πηa)]1/2 (Ⅰ-16) が得られる。 ブラウン運動による粒子の移動は、粒子の個数濃度の濃い方から希薄な方へと起こる。上式によると、ブラウン運動による拡散の速 さは、粒径 aが小さいほど速く、また粒子の平均速度 <x>はボルツマン分布に従い、温度 Tが高いほど拡散は速くなる。 図Ⅰ-14 ブラウン運動のシミュレーション (3) ブラウン運動と沈降 泥水のようなコロイドにおいて、泥の微粒子がなかなか沈降してこないのは、微粒子がブラウン運動をしているからである。重力に よって微粒子が沈降しても、ブラウン運動によって、微粒子は希薄になった上部へと拡散する。コロイド粒子が沈降して下部に沈積 してしまうか、液中に浮遊しているかどうかは、媒質の粘度にもよるが、主として粒径に依存する。粒径が大きいものは沈降して、 粒径が小さいものは拡散する。 式Ⅰ-14と式Ⅰ-16から計算した、水中における球形粒子(ρ/ρo = 2.5)のブラウン運動と重力沈降の比較を図Ⅰ-15に示す。粒子半 径が100nm付近(ao)で、移動距離と沈降速度が等しくなる。粒子径 a≪aoではブラウン運動が支配的となって粒子の分散状態が 継続し、a≫aoでは粒子は沈降することとなる。 a = 1μmレベルの粒子の沈降速度は3.6μm/sとなり、1mの深さに沈殿するのに3.2日を要する。上下左右の流れのある国内河川で は、雨天時の泥水を構成する微細な粒子は沈降することなく海に流れ込むこととなる。 図Ⅰ-15 水中における球形粒子のブラウン運動と重力沈降の比較a:粒子の半径[nm]、u:重力による沈降速度[m/s]、<x>:ブラウン運動による平均移動距離[m/s] 6.4 電気泳動 表面が正あるいは負に帯電しているコロイド粒子は、電極を入れて電圧をかけると、表面電荷と反対符号の極へと移動する。これを 電気泳動(electrophoresis)という。この現象から、コロイド粒子の表面が、正負どちらに帯電しているのかが決定できる。 例えば、水酸化鉄(Ⅲ)・Fe(OH)3コロイド溶液を電気泳動させると、Fe(OH)3のコロイド粒子は、ゆっくりと陰極の方へ移動する ので、Fe(OH)3のコロイド粒子は、正に帯電していることが分かる。一般に正に帯電しているコロイド粒子を含むコロイドを正コロ イド(positive colloid)、負に帯電しているコロイド粒子を含むコロイドを負コロイド(negative colloid)という。 粒子の移動は、粒子の大きさや形状、表面電荷、加えた電圧、pH、温度などによって影響され、異なるコロイド粒子を、移動速度の 差を使って分離することもできる。これは、タンパク質・DNA断片の分離・分析などによく用いられる。なお、疎水コロイドの電気 泳動の移動速度は比較的大きいが、親水コロイドは水和水のために、移動速度は小さい。 写真Ⅰ-3 DNA断片の電気泳動分析-活性汚泥・細菌群の16S-rDNA解析事例参考文献1) 池上 徹(栗田工業KCRセンター):水処理教室-凝集処理、https://kcr.kurita.co.jp/wtschool/012.html2) 化学工学協会編:化学工学便覧、丸善、19783) 北原 文雄・渡辺 晶:界面電気現象-基礎・測定・応用-、共立出版、19724) 北原 文雄:界面・コロイド化学の基礎、講談社、19945) 作花 済夫:ゾル-ゲル法の科学、アグネ承風社、19886) 小林 幹雄・他4名共編:数学公式集:共立出版、20057) 長谷川 裕也:コロイド化学、http://sekatsu-kagaku.sub.jp/colloid.htm8) 福田 清成・中垣 正幸:コロイド化学の基礎、大日本図書、19699) 古澤 邦夫:ぶんせき、5、247-254(2004)10) 粉体工学会編:液相中の粒子分散・凝集と分離操作、日刊工業新聞社、201011) 松村 淳司:界面・電気化学講義、http://res.tagen.tohoku.ac.jp/~liquid/MURA/kogi/kaimen/kaimen2002/2002-6.pdf12) 用水廃水便覧編集委員会編:用水・廃水便覧、丸善、197313) Alonso, M. and E. J. Finn, E.J.: University Physics-Volume Ⅱ Field and Waves, Addison-Wesley Publoshing Co., 196714) Bergdtrom, L.: Hamaker Constants of Inorganic Materials, Advances in Colloid and Interface Science, 70, pp.125- 169, 199715) Derjaguin, B.V.: Kolloid Z. (in German). Vol.69, No.2, pp.155–164, 193416) Hamaker, H.C.: Physica IV, No.10, 1058, 193717) Otterwill, RH & A. Watanabe: Kolloid. Z., Vol.170, p.133, Fig.1, p.135, Fig.4( 1960) Ⅱ.解 説解説(A) 粒子界面の静電気現象粒子に特異吸着しない成分から構成されるz-z型電解質(電解質)液中に、荷電粒子(例えば、正に帯電)が存在するとき、粒子表面近傍の溶液は電気的中和を保つため、図Ⅰ-5・Cに示したように、界面電荷と反対符号のイオン濃度(n–:単位体積中の負イオン個数[1/m3])が高く、逆に同符号のイオン濃度(n+:単位体積中の正イオン個数)が低くなって、正と負のイオンの個数濃度差Δn(= n– – n+)が生じる。一方で、熱運動による拡散作用によって、正負のイオンは同一の個数濃度になろうとする。このように相反する静電気作用と熱拡散作用が働くが、界面から離れるにしたがって静電気作用は減衰して、ついには拡散作用のみとなるので、表面から遠く離れたところでは正負のイオン個数濃度は同一(n+ = n– = n∞)となり、正負イオンの濃度差Δnは消失する。<イオン数濃度> 拡散電気二重層内において電位Ψ[V]を示すある微少体積Δv中の正負イオンの個数濃度は、Boltzmann分布に従うので、それらの個数濃 度は次式で示される。 n+ = n exp[- zeΨ/(kT)] n– = n exp[zeΨ/(kT)] (A-1) n(= n∞):母液中の電解質の個数濃度[/m3]、 n+・n–:拡散二重層内における正・負イオンの個数濃度[/m3]、 z:z-z型電解質のイオン価数、e:素量電荷(1.60×10-19[C])、 k:ボルツマン定数(1.38×10-23[J/K])、T:絶対温度[K]<Poisson式> 拡散層内における電位Ψの変化は、次のPoissonの式で示される。 ∇2Ψ = – ρ/ε (Ⅰ-2) ρ:電荷密度[C/m3]、ε:水の誘電率 (7.08×10-10[N/m2/C2]、25℃)<電荷密度> 上式(Ⅰ-2)に示す電荷密度ρは、単位体積中の正負イオンの個数差にイオン電荷量zeを乗じて求められるので、式(Ⅰ-2)中の ρ は、式(A- 1)を用いて次式で示される。 ρ = ze(n+ – n–) = nze{exp[-zeΨ/(kT)] – exp[zeΨ/(kT)]} = – 2nze・sinh[zeΨ/(kT)] (A-2)<電位変化> ここで扱う電気二重層モデル(a≧1/κ)では界面を近似的に平面として扱うので、界面からその法線方向の溶液側にx軸をとると、式(A- 2)を式(Ⅰ-2)に代入すると、次式が得られる。 d2Ψ(x)/dx2 = (2nze/ε)×sinh[zeΨ(x)/(kT)] (A-3) 式(A-3)を x = ∞ (Ψ = 0) ~ x = 0 (Ψ= Ψo) の範囲で積分すると、次式が得られる。 tanh[zeΨ(x)/(4kT)] = γexp(-κx) (A-4) γ = tanh[zeΨo/(4kT)] (A-5) 式(A-4)を変形すると、界面電位Ψoを有する荷電粒子の表面から距離x(x≦a)における電気二重層の電位Ψ(x)は、次式で示される。 Ψ(x) = 2kT/(ze)・ln[1 + γexp(-κx)]/[1 – γexp(-κx)] (A-6) 式(A-6)が求めるΨ(x)であるが、特に電位の低いzeΨo≪4kT(25℃で4zeΨo≪104mV)であるならば、式(A-6)のln[1 + γexp(-κx)]/[1 – γexp(-κx)] = 2γexp(-κx)となる(Debye-Hukel近似)ので、次式のように簡略化される。 Ψ(x) = 4kT/(ze)・γexp(-κx)] (A-7) したがって、式(A-3)は、次式のように簡易化される。 d2Ψ(x)/dx2 = κ2Ψ(x) (A-8) 式(A-8)を、式(A-4)を求めた同じ範囲で積分すると、式(A-4)の近似式として、次式が得られる。 Ψ(x) = Ψo exp(-κx) (Ⅰ-3)<留意事項> 電解質溶液中の分散粒子について、Boltzmann分布の式(A-1)およびPoissonの式(Ⅰ-2)を用いて正確なΨ(x)を求めることは困難を伴う ことから、球状粒子に限らず、様々なモデルに基づくΨ(x)を示す式が提案されている。また、実際に固液界面の構造は複雑であること、 また、導電性電極では固液界面の電位Ψoが測定可能であるが、分散粒子の表面電位の測定は困難である。実際に測定可能な電位は、荷電 粒子の動電現象による ζ-電位(図B-1、参照)である。また、現実の界面現象は、無機・有機の共存物質やpHによって様々な影響を受 け、厳密な定量的な解析は複雑となる。したがって、水浄化の現場での凝集分離およびその操作条件は、ジャーテストによって実験的に 確認され、その操作条件が決定される。 以上のような理由により、水浄化分野における分散粒子の数量的取扱いにおいて、疎水性コロイド粒子に対しては、その挙動や傾向は近 似式(Ⅰ-7)・(Ⅰ-8)で概略的な説明が可能である。疎水性粒子についての数量的取扱いは、前編Ⅰ-3や本解説(A)・(B)で記載している が、疎水性でない粒子の界面近傍の数量的扱いについては、複雑となるので省略する。<電気二重層の厚さ> κ[/m]は二重層電位ψの変化を決める重要な量で、1/κ[m]は電位ΨがΨo/exp(1)に低下す表面からの距離を示すので、二重層の拡がりの 指標となり、1/κを二重層の厚さまたはDebye長さという。式(A7)によると、NaCl水溶液では、1mmol/Lで10nm、0.l mol/Lで1nmと 推定される。 z-z型電解質の濃度と電気二重層の厚さを表A-1に示す。 2価・3価の金属イオンは配位水を有し、pHの上昇により酸解離してOH–が配 位した錯イオンを形成し、予想される1/κよりも大きい値となることに留意する(詳しくは、解説(D)-1.電解質効果)。 表A-1 電解質溶液の電気二重層の厚さ解説(B) 疎水性2粒子系の相互作用本解説(B)では、前解説(A)で扱った「疎水コロイド界面の電気二重層」に基づき、水溶液中で2つのコロイド粒子が接近したときの相互作用を数量的に扱う。最初に、コロイド系のモデルと相互作用の結論を示し、この結論に至る説明を行う。なお、コロイドに関する本モデルは、次の条件に限定したものとする。・水溶液内の荷電粒子は球状で、表面電位Ψoとする。ただし、単原子イオンなどÅレベルの小さなイオンが特異吸着している場合には、 Stern電位ΨδをΨoとする(図B-1を参照)。・荷電粒子は疎水性とし、粒子表面に水和層の形成はなく、さらに、特異的に吸着する複雑なイオン(界面活性剤イオン、高分子イオン、 高原子価イオン、錯イオンなど)は共存しないものとする。・水溶液内に共存する正負イオンはz-z価の対称電解質が完全解離したものとする。・電気二重層の厚さ(1/κ)は10nm以下(例えば、NaCl濃度>1mmol/L)で、ここで扱う粒子の半径 aは100nm~1μm程度とすると、2 粒子が接近してそれらの電気二重層が重なったとき、その重なり領域に対応する粒子表面は近似的に平面(具体的には円板)として扱う ことができるものとする(a≫1/κ)。<電気二重層のモデル> 様々な電気二重層モデルが提案されているが、代表的をものを、次の図B-1に示した。 Helmholtzは金属表面の電荷と、これを中和する溶液中のイオンが向かい合って並んでいるいて、これを平行コンデンサーが形成される ようなモデルを考えこれを電気二重層と呼んだ(図B-1・A)。 次に、イオンには熱運動を行って均一に分布する作用が働く。したがって、界面近傍の過剰な対イオンは、重力場内の分散系粒子の沈降 平衡に似た拡散的な分布をとる。このことから、二重層内の電位低下は界面付近で急激で、界面から遠ざかるにつれてなだらかとなる。 これをGouy-Chapmanの拡散二重層のモデルである(図B-1・B)。 しかし、このような拡散二重層のみによって計算した値は、測定値よりも一桁大きく、むしろHelmholtzのモデルによる値がずっと測定 値に近い。この矛盾を解決するために、Sternは金属表面のすぐ近くにはイオンの特異吸着(Stern層)があって、この外側にGouy- Chapmanの拡散二重層が広がっているようなモデルを考えた(図B-1・C・D)。 このような表面の電荷と帯電粒子の固定相、および拡散二重層を総括して界面電気二重層と呼ばれる。本モデルで取り扱う対称は、この 図中の(B)または(C)とする。 図B-1 粒子と電解質溶液の界面近傍における電気二重層のモデル<コロイド粒子の分散と凝集> 一般に、水中の微細粒子はその表面が帯電していて、その静電的反発力によって粒子の凝集作用が阻害され、ブラウン運動により水中に 分散している。ところが、pH変化や電解質添加によって、凝集して粗大粒子(約10μm以上)となるとブラウン運動よりも重力作用が大 きくなって沈降(または浮上)したりする(図Ⅰ-15、参照)。ここでは、ブラウン運動の影響が大きい100nm~1μ前後の粒子をモデル として取り扱う。 粒子間には、静電気的反発力(分散力)PR [N/m2]とvan der Waals引力(凝集力)PA [N/m2]の2つの相互作用が働き、これらの合 力は次式で示される。 P= PR + PA (Ⅰ-4) 一方で、コロイド系の安定性は、その系の状態を分散エネルギーVR[J]および凝集エネルギーVA [J]を総和した自由エネルギーVに依存 する。 V = VR +VA (Ⅰ-5) 本章の冒頭に記載した電気二重層モデルの条件下では、半径 a[m]の2個の荷電粒子が、遠くから粒子界面距離 h[m](<a)に接近した ときの相互作用力P(h)および自由エネルギーV(h)は、次式で近似的に示される。 P(h) = 2πaεκΨo2 exp(-κh) – aA/(12h2) (Ⅰ-7) V(h) = 2πaεΨo2 exp(-κh) – aA/(12h) (Ⅰ-8) κ2 = 2nz2e2/(εkT) (Ⅰ-9) κ = 3.3×109z√C [/m] (T = 298K) (Ⅰ-10) ここで、式(Ⅰ-7)~式(Ⅰ-10)において、Ψo:粒子-水界面における電位[V]、ε:水の誘電率(7.08×10-10[N/m2/C2]、25℃)、A: Hamaker定数、z:z-z型対称電解質の価数、n:単位体積中の電解質イオン個数[1/m3](n = n∞:図Ⅰ-5・C、参照)である。 なお、25℃の水溶液では、電荷質濃度C[mol/L]とすると、n = 103NAC[/m3] (NA:Avogadro定数、6.02×1023[/mol))である ので、式(Ⅰ-9)は式(Ⅰ-10)で示される。 式(Ⅰ-7)・式(Ⅰ-8)に基づいて、試算した結果の事例を図Ⅰ-6~図Ⅰ-8に示した。これらの式の導入過程にあっては様々な近似と簡略化 が行われているが、コロイド粒子の水溶液中における挙動の概要を説明できる。以下に、これらの式の導入過程について解説する。詳し くは、ページボトムに記載の参考文献(北原・渡辺, 1972、北原, 1994や粉体工学会, 2010など)を参照されたい。<計算ソフト> 参考までに、式(Ⅰ-7)・式(Ⅰ-8)に各パラメーターの値を入力して実際に計算し、その結果を図示するExcelファイルを本サイトのサーバ ーに保存してあるので、目次-付録からダウンロードして試算されると理解が深まると思われる。具体的な粒子のHamaker定数は数多く 求められているので、文献(Bergdtrom, 1997や粉体工学会, 2010)を参照されたい。1.荷電粒子間の静電相互作用 水溶液中で、荷電粒子が互いに接近すると、両者の電気二重層に重なりが生じ(前記図Ⅰ-5・D)、重なり領域の対イオン個数濃度を増 加させる。この結果、表面荷電の静電気的反発作用に加えて、この領域の浸透圧Π[N/m2]が増加して自由エネルギー(= Πv [Nm=J]、 v:重なり領域の体積)が増大することとなる。 しかし、2つの粒径粒子の二重層の重なりによる自由エネルギーの増加量の計算はかなり複雑である。そこで、粒子径 a(100nm以上) が二重層の厚さκ(10nm前後)の10倍以上、すなわち、a≫1/κであれば、二重層の重なりを2枚の同符号に荷電した平行板に近似して扱 うことができる(電気回路で多用されるコンデンサーの極板は正負の対符号で帯電していることが大きな相違である)。多くの場合、こ の近似モデルでその概略を満足に説明できる結果が導かれる。 ここで、2枚の同サイズ・同符号に帯電の平行板の単位面積あたりに働くは力Pp[N/m2]は式(B-1)に示すように静電気力Peと浸透圧Po の和となり、PeとPoは、それぞれ式(B-2)および(B-3)で示される。 Pp = Pe + Po (B-1) Pe = -(ε/2) (dΨ/dx)2 (B-2) Po = (n+ + n–)kT – 2nkT (B-3) 一般に、Poは常にPeよりも大きく、さらに二重層の重なりによって表面電位Ψoに変化がなければ、Peを無視できる。この理由は、同 サイズで同符号に帯電した平行板であれば、それらの中間距離での面上では、その対称性から電界[V/m]はdΨ/dx = 0となり、Poのみを 考えればよいこととなる。1.1 荷電平行板の静電相互作用(Derjaguin近似) 式(B-1)(≒ 式(B-3))に式(A-1)を代入すると、平行板に働く単位面積あたりの力Pp(h)は、次式で表される。 Pp(h) = 2nkT{cosh[zeΨ(h/2)/(kT)] – 1} (B-4) h:2平行板間の距離[m]、Ψ(h/2):中間点における電位[V] 式(B-4)は複雑であるので、以下に示す近似を行う。 電位が低く、また電位の重なりが余り大きくない条件では、図B-2に示すように、式(A-6)で表される単独粒子の電気二重層の電位 Ψ(h/2)の2倍に相当するものと考えると、Ψp(h/2) = 2Ψ(h/2)、となる。 次に、zeΨ/4kT≪1の時には、解説(A)の式(A-7)の近似式にx = h/2を代入すると、次式が得られる。 Ψp(h/2) = 2Ψ(h/2) = 8kT/(ze)・γexp(-κh/2) (B-5) γ= tanh[zeΨo/(4kT)] (A-5) ここで、 式(B-4)の右辺のcosh項についてテイラー展開して3次項までの近似、cosh y ≒ 1 + (1/2)y2、を用い、この近似式に式(B-5) を代入すると、次式が得られる。 cosh[zeΨ(h/2)/(kT)] ≒ 1 + (1/2)[zeΨp(h/2)/(kT)]2 = 1 + 32γ2exp(-κh) 上式を式(B-4)に代入すると、次式で示される。 Pp(h) = 64nkTγ2 exp(-κh) (B-6) 以上のことから、同サイズの2枚の平衡した荷電平行板を遠距離∞からhまで接近させたときの単位面積あたりの必要エネルギー Vp[J/m2]は、式(B-6)を積分すると、次式で表される。 Vp(h) = -∫Pp(h)dh (h = ∞ → h) = (64nkTγ2/κ)exp(-κh) (B-7) 図B-2 同符号に荷電した2枚の平行板による電気二重層の重なり1.2 2粒子間にはたらく静電相互作用 粒子間の静電相互作用は、粒子半径 aとデバイ長の逆数κとの積κaの大きさによって基礎式もその近似解法も異なる。 図Ⅰ-5・Dに示すように、本モデルの条件(a≫1/κ)では電気二重層の厚さが小さいので、Deriaguin近似を導入して球を半径 aの薄い 円板と考えると、この2枚の円板間の静電相互作用力FR(h)は、次式で示される。 FR(h) = 2π{a2/(a+a)}Vp(h) = πaVp(h) (B-8) 式(B-7)を上式に代入して、h = ∞ → h の範囲で積分すると、静電相互作用によるVRエネルギーとして、次式が得られる。 VR(h) = 64πankTγ2/κ2 exp(-κh) (B-9) 式(B-10)についても同様に計算するか、または、PR(h) = – dVR(h)/dhからも求められる。 PR(h) = 64πankTγ2/κ exp(-κh) (B-10) 解説(A)の式(A-5)において、zeΨo/(4kT)≦1のとき、γ = tanh[zeΨo/(4kT)] ≒ zeΨo/(4kT)となり、この近似したγと式(Ⅰ-9)で示す κを上記の式(B-9)・(B-10)にそれぞれ代入すると、次の近似式が得られる。 PR(h) = 2πaεκΨo2 exp(-κh) (B-11) VR(h) = 2πaεΨo2 exp(-κh) (B-12)1.3 本モデル以外のコロイド系<厚い二重層または小粒子系:a<1/κ > このケースでは、Deriaguin近似が適用できず、Debye-Hueckel近似を適用した次の式が得られている。 VR(h) = 4πεΨo2a2/(h + 2a)・exp(-κh) (B-13)<広範囲のκaへ適用可能な式> Debye-Hueckel近似のもとで、粒子間のPoisson-Boltzmann方程式の近似解から得られた次式が提出されている。 VR(h) = 4πεΨo2a(h + a)/(h + 2a)・ln[1 + a/(h + a)・exp(-κh)] (B-14) 式(B-14)は、近距離 h≪aでは、a≫1/κの式(B-12)になる一方、遠距離 h≫aではa<1/κの式(B-13)に収束するので、広範囲のκaに適用 可能と考えられている。2.粒子間のvan der Waals相互作用 2つの原子間に働くLondon-van der Waal力は短距離力でそのポテンシャル力はその原子間距離の6乗に逆比例するので、遠距離におい てはその作用は働かない。しかし、コロイド分散系の各粒子には極めて多数の原子が含まれているので、これらの相互作用を加え合わせ ると、原子間に比べて粒子間引力は遠方にまで作用することとなる。 Hamker(1937)は、2枚の平行板および球形粒子間に働く引力のポテンシャルエネルギーVAを計算した。球形粒子間については、次 式で示した。 VA = – (A/6){2/(S2 – 4) + 2/S2 + ln(s2-4)/s2} (B-15) ここで、s = 2a + h、a:粒子半径[m]、h:粒子の最短表面間距離[m] である。a≫hの場合には、次式で近似される。 VA = – aA/(12h) (B-16) なお、2粒子間の引力PAは、式(A-16)を微分して次式で示される。 PA = aA/(12h2) (B-17) 解説(C) 粒子界面電荷の発生解説(D) 電解質効果とSchulze-Hardy法則図D-1 AgIの陽性ゾルにアルキル硫酸ナトリウムの添加濃度とζ-電位の関係測定値(Otterwill & Watanabe, 1960)を次式でフィッティングした。ζ = ζo tanh[(X – b)/a]、X = log xζo:120[mV]、x:添加濃度C[mol/L]、C10:a = 1.6;b = -3.2、C12:a = 1.0;b = -4.4、C14:a = 0.8;b = -4.8図D-2 AgIの陽性ゾルにアルキル硫酸ナトリウムの添加濃度と安定度比(W)の関係測定値(Otterwill & Watanabe, 1960)を次式でフィッティングした。Log W = c {cosh[a(X – b) – 1}、X = log xC10:a = 2.0;b = -3.2;c = 0.8、C12:a = 1.0;b = -4.2;c = 3.8、C14:a = 0.5;b = -4.8;c = 16表D-1 分散コロイドの臨界凝集濃度cfc [mmol/L]解説(E) 凝集速度解説(F) 表面張力と界面活性図F.1 表面張力のモデル実験図F.4 曲面における気相・液相の全圧(Pg、Pl )の違い液面:(a) 凹面(r>0)、(b) 凸面(r<0)、(c) 平面図F.5 図F.4(a)に対応する凹状液面のモデル図図F.7 油・水の界面の分子に働く力 [Fowkes, 1964]大きい○:油分子、小さい○:水分子図F.8 水溶液の表面張力と溶質濃度との関係の模式図図F.9 α相とβ相との界面のモデル図領域AABBが界面相、本文ではβ相は空気として無視している図F.10 界面活性剤水溶液のcmcにおける模式図解説(G) 界面活性剤の特性図G.1 界面活性剤の模式図A:疎水基、B:親水基、C:酸化エチレン基図G.2 界面活性剤の機能の模式図(a) 泡立て、(b) 油の乳化、(c) 固体粒子の分散図G.3 (a)ミセル、(b)逆ミセルの模式図逆ミセルを作るものは二重鎖型が多い表G.1 界面活性剤のクラフト点Tkの事例図G.4 イオン性界面活性剤の水への溶解度を示す模式図Tk:クラフト点図G.5 ドデシル硫酸ナトリウム水溶液の物性の濃度変化(25℃)A:モル導電率、π:浸透圧、γ:表面張力、γ’:油との界面張力、τ:濁り度注)非イオン界面活性剤のcmcは溢度で著しく変化する。cmcを求める方法によりcmcはいくぶん変わることがある。表G.2 界面活性剤水溶液のcmc [mol/L]図G.7 界面活性剤分子の形状に関するパラメーター図G.8 界面活性剤濃度と難水溶性物質(油・染料)の可溶化量図G.9 O/Wマイクロエマルジョンの模式図図G.10 可溶化状態図の一例一定濃度の界面活性剤の水溶液に油を添加し、温度を変えて溶解する領域を調べる図G.11 オクチル硫酸ナトリム・ヘキサノール・デカン・食塩水系でのマイクロエマルジョン(ME)の生成解説(H) 吸着エネルギーと平衡式表H.1 物理吸着と化学吸着の差異図H.1 吸着等温線の4つ型(a) Langmuir 型、(b) BET 型、(c) Freundlich 型、(d) 階段型図H.2 2つの吸着等温線から吸着熱を求める操作図H.3 吸着速度過程におけるエネルギー関係E+:吸着の活性化エネルギー、E–:脱着の活性化エネルギー、Ha:吸着熱図H.4 Langmuirの吸着式のパラメータ(a、Am)の決定図H.5 吸着等温線への溶媒効果(相対量での比較)(a) 水-活性炭系、(b) トルエン-シリカゲル系C1:酢酸、C2:プロピオン酸、C3:酪酸図H.6 高分子の3つの吸着形態(a) 水平型(train)、(b) 垂直型(tail)、(c) ループ型(loop)解説(J) 高分子吸着と分散・凝集図 J.1 粒子表面への吸着高分子のモデル図図 J.2 粗な吸着高分子による粒子間の橋かけ凝集のモデル図(a):粒子表面への粗な高分子吸着、(b):吸着高分子の橋かけによる粒子の凝集図 J.3 密な高分子吸着層による反発作用のモデル図(a):粒子を覆う密な高分子吸着層、(b):粒子接近での高分子吸着層の重なりによる反発作用図 J.4 高分子濃度と凝集・分散作用の関係W:安定度比、Wo:高分子濃度 ’0’におけるW、W<Wo:凝集、W>Wo:分散図 J.5 吸着層を有する2粒子系のポテンシャルエネルギー曲線を示す一例図 J.6 枯渇凝集の原理を示す模式図図 J.7 電気二重層と吸着層の共存効果のモデル図(a):橋かけ凝集が起こる(δ>2/κ、δ>h)、(b):橋かけ凝集が起こらない(δ<2/κ)株式会社ジャパンフォーシーズンズ ( Japan Four Seasons Co., Ltd. )本 社 〒343-0023 埼玉県越谷市東越谷2-11-7大阪営業所 〒532-0011 大阪府大阪市中央区内本町1-2-15 谷四スクエアビル7階 ㈱ブリックス内TEL・FAX 048-966-9294E-mail:[email protected]:https://www.jfs-trading.com➣情報セキュリティーポリシー ➣プライバシーポリシーCopyright © 2016 by Japan Four Seasons Co., Ltd. All Rights Reserved.




![はじめての 1-Wire® [その他機能・注意事項編]](https://www.marubun.co.jp/wp-content/uploads/2022/09/ffc98ef796cfbb0960227eb19987c462.jpg)





![アサヒ スーパードライ 缶(500ml*24本入)【2shdrk】【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]](https://thumbnail.image.rakuten.co.jp/@0_mall/soukaidrink/cabinet/806/4901004006806.jpg?_ex=300x300)















![アサヒ スーパードライ 缶(350ml*48本セット)【アサヒ スーパードライ】[アサヒビール/ビール/スーパードライ]](https://thumbnail.image.rakuten.co.jp/@0_mall/soukaidrink/cabinet/557/62557.jpg?_ex=300x300)