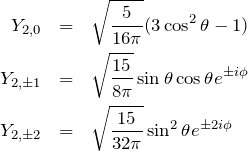Images of ハートレー

087DSC09293.jpg view page

【最大7000円オフクーポン】【中古】iPhone SE 第3世代 2022 SE3 A2782 64GB 128GB スマホ スマートフォン SE3 本体 SIMフリー ミッドナイト レッド…view page

ブレンドン・ハートレー「明日に向けてポジション改善の余地あり」 view page

〈レッド・カーペット〉 ニーナ・ホス＝ロイター view page

GILFs view page

【最大2000円クーポンGET】「新品 未開封品 」SIMフリー iPhone14 Pro Max 128GB Gold ゴールド ※赤ロム保証…view page

#ニーナ - Twitter検索 / Twitter Japanese Beauty, Japanese Girl, School Looks, Girls Uniforms, Beautiful Asian Girls, Cute Girls, Korea, Kawaii, Young view page

紀伊國屋書店 view page

Кира Найтли / Keira Knightley / фото актера view page

iPhone 16e simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン 【ご注文から30分経過後はキャンセル不可】【自宅受け取り限定…view page

Nina view page

ブレンドン・ハートレー、レッドブルのリザーブドライバーに決定 view page

F1 ブレンドン・ハートレー トロロッソ・ホンダ view page

【ふるさと納税】200-3【選べるカラー】高性能リユース　スマホ　Apple　iPhone 13 128GB　SIMロック解除済　本体のみ ｜ 中古 再生品 本体 端末view page

ブレンドン・ハートレー view page

ブレンドン・ハートレー「ドライバーとして、人として成長出来た一年だった」 view page

ブレンドン・ハートレー、残留に手応え「2ポイントに相応しい攻めの走りが出来た」 view page

【最大7000円オフクーポン】純正バッテリー100%｜90%【中古】iPhone 14 128GB 256GB 512GB A2881 スマホ スマートフォン 本体 SIMフリー ミッドナイト…view page

ブレンドン・ハートレー、F1デビューにむけて50ページのマニュアルを熟読 view page

ブレンドン・ハートレー view page

F1 ブレンドン・ハートレー トロロッソ・ホンダ view page

iPhone 17 端末本体のみ(機種変更はこちら) SIMフリー 新品 純正 Apple 認定店 楽天モバイル公式 アイフォン 【ご注文から30分経過後はキャンセル不可】【自宅受け取り限定 /…view page

N0050_A view page

F1 ブレンドン・ハートレー トロロッソ・ホンダ view page

F1 ブレンドン・ハートレー トロロッソ オーストラリアグランプリ 2018年のF1世界選手権 view page

【ふるさと納税】135-1【選べるカラー】高性能リユース スマホ Apple iPhoneSE 3 64GB SIMロック解除済 本体のみ ｜ 中古 再生品 本体 端末view page

ブレンドン・ハートレー、スーパーライセンスを取得できず view page

F1 ブレンドン・ハートレー トロロッソ・ホンダ ホンダF1 view page

F1 | 【動画】サスペンショントラブルでクラッシュを喫したハートレー／F1イギリスGP FP3 view page

[国内版SIMフリー・新品未開封/未使用品] iPhone15 128GB 256GB 512GB 各色 スマホ 本体view page

F1 トロロッソ・ホンダ ブレンドン・ハートレー view page

F1 ブレンドン・ハートレー トロロッソ・ホンダ view page

F1 ブレンドン・ハートレー トロロッソ・ホンダ view page

iPhone 15 simフリー 端末本体のみ （機種変更はこちら） 新品 純正 Apple 認定店 楽天モバイル公式 アイフォンview page

ハートレー・マグニアイヤー view page

フォーミュラE：ハートレー、GEOXドラゴンと契約締結。2019／20年デビューへ。 view page

ブレンドン・ハートレー、シート喪失の一端を語る「F1には多額のお金と政治が渦巻いている」 view page

【4日20時からポイントUP! スーパーSALE】新品未開封品【Nランク】SIMフリー iPhone17 256GB ブラック MG674J/A ホワイト MG684J/A ミストブルー…view page

CQ出版社 オンライン・サポート・サイト CQ connect view page

ブレンドン・ハートレー、トロロッソ・ホンダ残留に手応え view page

クラブハーレー賞おめでとうございまーす。 view page

[新品未開封｜未使用品｜SIMフリー] iPhone 16e 128GB 256GB 512GB ホワイト ブラック アイフォン16e 本体 iPhone16e 端末 スマホview page

現代とはいつから view page

現代とはいつから view page

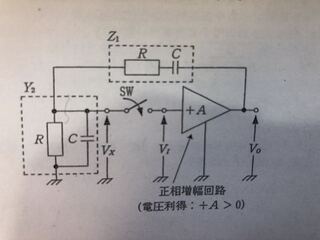
Yahoo!知恵袋次の図のようなRC発振回路において、Z1はRとCの直列回路のインピーダンス、Y2はR とC の並列回路のアドミタンス、Aは正相増幅回路の電圧利得を示したものであり、すいっちSW を閉じると発振する。この発振回路につい view page

【最大7000円オフクーポン】【中古】iPhone 14 128GB 256GB 512GB A2881 スマホ スマートフォン 本体 SIMフリー ミッドナイト (PRODUCT)RED…view page

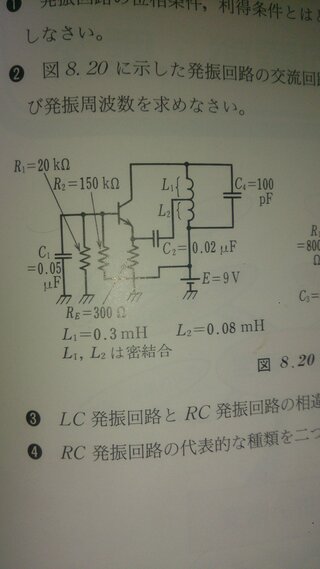
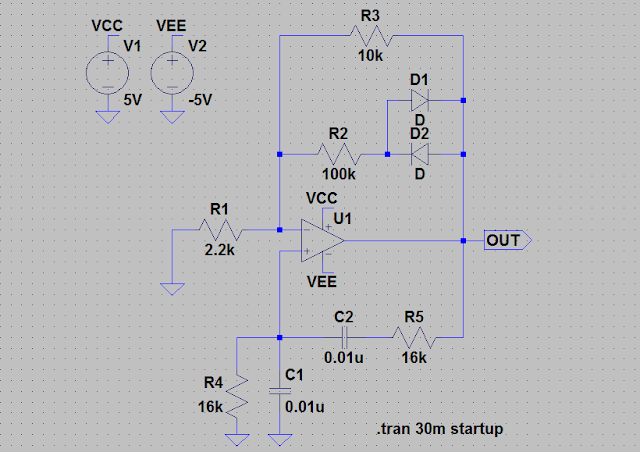
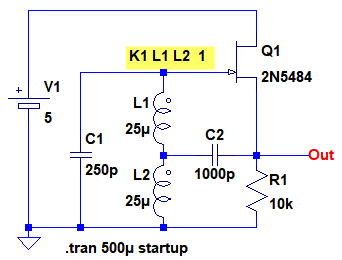
Yahoo!知恵袋電気回路について 画像のハートレー発振回路の発振周波数なのですが、600～700kHzくらいの値になるハズなのですが何回やっても800kHzくらいになって計算が合いません。 導出過程を教えてくだ view page

音源とオーディオの電子工作（予定） view page

F1デビュー戦のハートレー、パワーユニット交換でグリッド降格へ view page

【ふるさと納税】130-2【選べるカラー】高性能リユース　スマホ　Apple　iPhone 12 64GB　SIMロック解除済　本体のみ ｜ 中古 再生品 本体 端末view page

ブレンドン・ハートレー view page

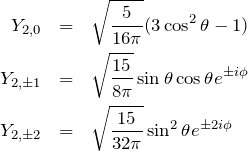
\begin{eqnarray*} Y_{2,0} &=&{\sqrt\frac{5}{16\pi}}(3\cos^2\theta-1)\\ Y_{2,\pm1} &=&\sqrt{\frac{15}{8\pi}}\sin \theta\cos\theta e^{\pm i\phi}\\ Y_{2,\pm2} &=&\sqrt{\frac{15}{32\pi}}\sin ^2\theta e^{\pm 2i\phi} \end{eqnarray*} view page