Images of 対角行列

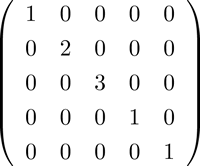
「京」を使い世界最高速の固有値計算に成功－超巨大行列の固有値を１時間で計算－ view page

固有値・固有ベクトルと行列の対角化 [ 長谷川雄之 ]view page

行列力学について８枚のスライドでまとめてみたら view page

画像に alt 属性が指定されていません。ファイル名: image-18.png view page

数理助教の会 view page

これからの線形代数 3重対角化 特異値分解 一般逆行列[本/雑誌] / 藤岡敦/著view page

[Pythonによる科学・技術計算]行列の固有値問題のロードマップ，数値線形代数はじめにどんな人向け？内容1. 固有値問題2. 相似変換に着目3. 中間形への変換中間形へ変換しない解法: ヤコビ法，べき乗法QR法QR分解参考文献 view page

160604b view page

行列の対角化とは？意味と方法と使い方[練習問題付き] view page

【中古】 図解でわかる線型代数 ベクトル、行列の計算から写像、固有値、対角化まで / 野崎 亮太 / 日本実業出版社 [単行本]【メール便送料無料】【最短翌日配達対応】view page

対角行列の性質 view page

勉強しよう数学3C view page

（線形代数）行列の対角化を用いた応用及び図形的な意味～行列のn乗と楕円体の方程式～ view page

【中古】 図解でわかる線型代数 ベクトル、行列の計算から写像、固有値、対角化まで / 野崎 亮太 / 日本実業出版社 [単行本]【宅配便出荷】view page

（線形代数）行列の対角化を用いた応用及び図形的な意味～行列のn乗と楕円体の方程式～ view page

matrix3_4 view page

対角行列の性質 view page

行列の対角化可能性と同値な条件とは：証明、判定法 view page

基底と座標と対角化 view page

行列の対角化 view page

【中古】 図解でわかる線型代数 ベクトル、行列の計算から写像、固有値、対角化まで / 野崎 亮太 / 日本実業出版社 [単行本]【ネコポス発送】view page

【対角行列】固有値方程式の固有値と固有ベクトルから対角行列をつくる view page

行列式の性質6つの証明(列,行の線形性,置換,積,転置など) view page

勉強しよう数学3C view page

数学基礎プラスγ(線形代数学編)〈2015〉―行列の対角化とその応用view page

【入門線形代数】行列の対角化-標準化- view page

f:id:simplestar_tech:20170412084653g:plain view page

勉強しよう数学3C view page

【中古】 図解でわかる線型代数 ベクトル、行列の計算から写像、固有値、対角化までview page

勉強しよう数学3C view page

第1回Python3データ分析模擬試験【第10問】解説 view page

Python3ではじめるシステムトレード：SVD step by step AとS view page

【中古】 図解でわかる線型代数 ベクトル、行列の計算から写像、固有値、対角化までview page

情報科学科２年生応用線形代数 のための MATLAB 入門 view page

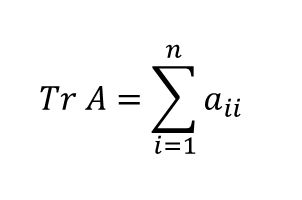
正方行列の対角和（トレース）の性質 おーにし★読書会やってます！★一般相対論の読書会やってます。(オンライン)「一般相対性理論を一歩一歩数式で理解する」 途中からの参加も歓迎！サイト内検索記事別・拍手数ランキング記事別・アクセス数 週間ベスト5最近の投稿カテゴリー月別アーカイブ view page

対角行列の性質 view page

図解でわかる線型代数: ベクトル、行列の計算から写像、固有値、対角化まで 野崎 亮太view page

f:id:stchopin:20200927180950p:plain view page

掃き出し法による逆行列の計算の例題の解法 view page

勉強しよう数学3C view page

【中古】 図解でわかる線型代数: ベクトル、行列の計算から写像、固有値、対角化までview page

うさぎでもわかる線形代数　第18羽　対角化を用いた行列のn乗の求め方・行列の無限乗 view page

勉強しよう数学3C view page

サラスの公式で3次の行列式を求める方法を図解 view page

固有値・固有ベクトルと行列の対角化 長谷川 雄之view page

対角行列のイメージ図 view page

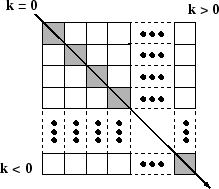
対角行列の作成と行列の対角要素の取得 Matlab Diag Mathworks 日本 view page

spdiags view page

【中古】 図解でわかる線型代数 ベクトル、行列の計算から写像、固有値、対角化までview page

行列の基礎知識②　【行列の種類】 view page

「行列の対角化②〜実対称行列、エルミート行列、正規行列の対角化〜」【線型代数学の基礎シリーズ】固有値編 その4 view page