Images of 条件収束

広義積分の収束条件 view page

【max25％OFFクーポンで825円】 日本製 ヘアドライタオル 綿100% ハービー Halfbe 楽天1位 / シルクプロテイン ドライヤー時間半分 【オギャ子さん×ヒオリエ…view page

3本の移動平均線収束個所表示インジケーター2 view page

Kernel-KmeansのNumpy実装 view page

緊急事態宣言　14日検討は早急か？解除の条件や収束への課題を考察 view page

[美容をトータルサポート♪]ナウフーズ ビオチン サプリメント 10mg (10000mcg) 120粒 NOW Foods Biotin ベジカプセル 120日分 ビタミンB群 スキンケア…view page

電磁界解析ソフトウェア電磁界解析ソフトウェア view page

ζ(4) view page

【数列の極限の大小関係】イメージでわかる、知っててアタリマエの公式 view page

【店内P最大18倍以上開催】14種類の豊富な成分により内側から環境をサポート【DHC直販】 ボリュームトップ30日分 | dhc サプリメント サプリ ボリュームトップ ヘアケア 髪…view page

広義積分の収束条件 view page

はじめてみよう！流体解析（入門編）［Ⅳ］～流体解析の作業工程～ view page

励振源・境界条件・収束判定・解析の実効値【電磁波解析の基礎用語】 view page

【送料無料】YASAI シャンプー750ml　or ヘアパック600g 大容量タイプ（専用読本付き）通常よりも3倍容量でお得なサイズココナッツ由来最高級洗浄成分配合TAMA Yasai…view page

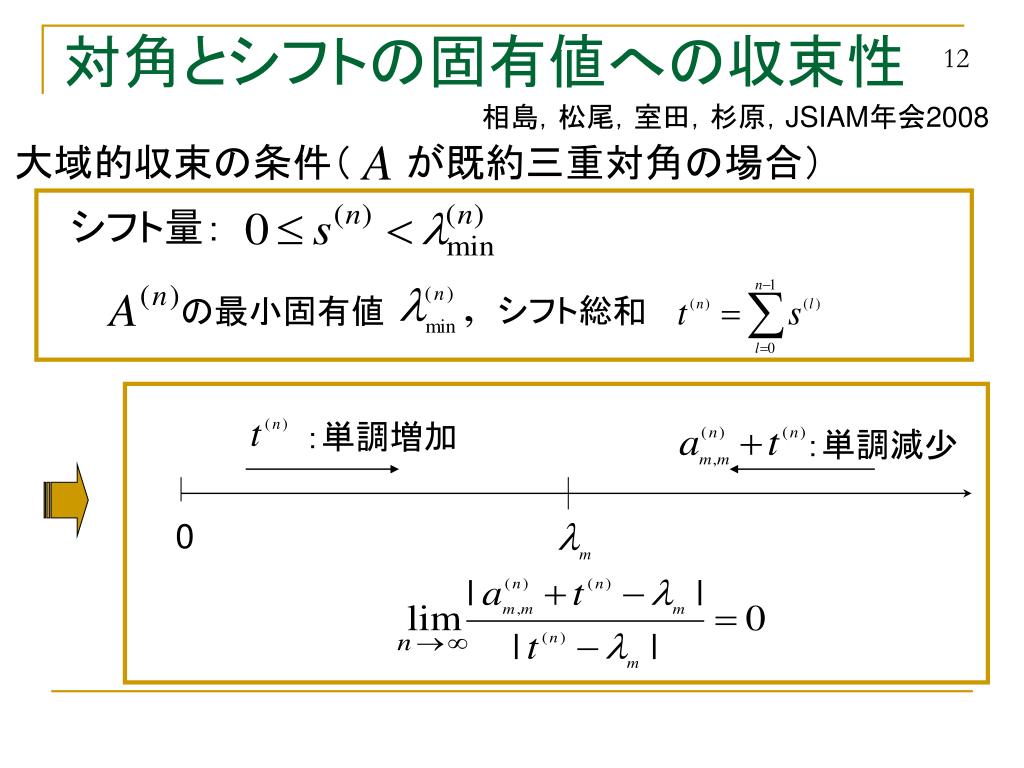
シフト付きコレスキー LR 法における ２つの固有値近似法の収束性について view page

身勝手な主張 view page

Yahoo!知恵袋この整級数の収束半径って何になりますか？ view page

トリートメントの素 ・100mL 髪の NMF 原料混合液 ケラチン 配合 トリートメントのもと 送料無料view page

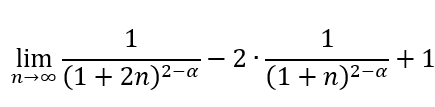
Yahoo!知恵袋電気回路、四端子定数についてです。 以下図5,6,7の二端子対回路において、F行列を解説込みで求めていただけないでしょうか。 与えられた値はR=1.5kΩ、C=1.0µF、f=1.2kHz。 view page

シフト付きコレスキー LR 法における ２つの固有値近似法の収束性について view page

条件収束級数は和の順序交換により任意の値に収束できることの証明 view page

【ふるさと納税】髪 すきバサミ 美容師 子供 散髪 貝印 セルフ 痛くない はさみ 【 関孫六 スキハサミ 】ヘアカット ハサミ 鋏 髪切 セルフカット 理美容 家庭用 美容院 髪切りはさみ…view page

条件収束級数は和の順序交換により任意の値に収束できることの証明 view page

反省会について view page

四ツ谷のバレリーナ専門気功整体「Rayまといのば」いくつも広がる世界線を、Goalに沿って意図することで選び、行きたい世界へ転生していきましょう！ view page

【楽天1位／レビュー1.3万件★4.64】ヘアブラシ Lefina 豚毛×天然木 高級パドルブラシ ヘッドスパニスト監修 頭皮ケア 頭皮マッサージ 静電気防止 髪質サポート 艶髪 乾燥対策 ギフト…view page

GSM 日本周辺 地上風流線/収束発散 view page

JavaScript is not available. view page

GSM 日本周辺 地上風流線/収束発散 view page

【高濃度 スーパーミレットエキス】お徳用 90粒 約3ヶ月分 ミレットエキス シスチン コラーゲン 亜鉛酵母 髪の毛 ギフト 贈り物 サプリメント ボリューム 美容 ツヤ コシ アミノ酸 通販…view page

図形を利用した定積分の計算 view page

6本の移動平均線収束個所表示インジケーター view page

【ディニの定理】各点収束から一様収束が従う定理とその証明 view page

【店内P最大18倍以上開催】【DHC直販】 美HATSUGA 30日分 | DHC サプリメント サプリ 健康食品 ケラチン 美容 ヘアケア 1ヶ月分 スカルプ スカルプケア 髪 ビタミンサプリ…view page

関数列の各点収束、一様収束とは、例と違い、求め方 view page

Yahoo!知恵袋英語で論文を書く場合、「式」（数式）はどのような英語で表記するのでしょうか？ 「formula」でしょうか？ view page

junologyのブログ 超関数の収束とδ関数の表式 view page

【公式】タングルティーザー ザ・アルティメットディタングラー ヘアブラシ 正規品view page

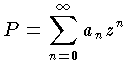
収束半径（読み）しゅうそくはんけい（英語表記）radius of convergence view page

画像 view page

画像 view page

【UCHINO公式店】ウチノ とってもよく吸う「ごくふわ」 ヘアータオル｜内野 タオル 綿100% コットン 抗菌 防臭 吸水 速乾 軽い やわらか ふわふわ 小さめ ヘアタオル ヘアキャップ…view page

Yahoo!知恵袋線形代数の部分空間であることを証明する問題です。 次のw ⊂R^3について w = {[x,y,z] | z^2 = x^2 + y^2} を部分空間であると証明したいです。 view page

级数2的n次方*(x的2n次方)的收敛半径？级数2的n次方*(x的2n次方)的收敛半径？ view page

画像 view page

初体験！圧倒的ヘアオイル誕生！【送料無料】髪サラダ ●新ヘアオイル●ひとぬりの感動 たったの10秒で驚く髪へ 圧巻のヘアオイル遂に新誕生アルガンオイルを始め、贅沢植物オイル配合|コスメ…view page

画像 view page

画像 view page

画像 view page

髪の毛ポイ捨てシール 浴室排水口用 大サイズ(直径15cm) 10枚入 (100円ショップ 100円均一 100均一 100均)view page

2014年度秋学期　応用数学（解析）　第１部・「無限」の理解　／　第４回　収束とは何か，ε-δ論法 (2014. 10. 16)2014年度秋学期　応用数学（解析）　第１部・「無限」の理解　／　第４回　収束とは何か，ε-δ論法 (2014. 10. 16) view page

lim(n→∞) Σ(k=1,n) n*(5/6)^n view page