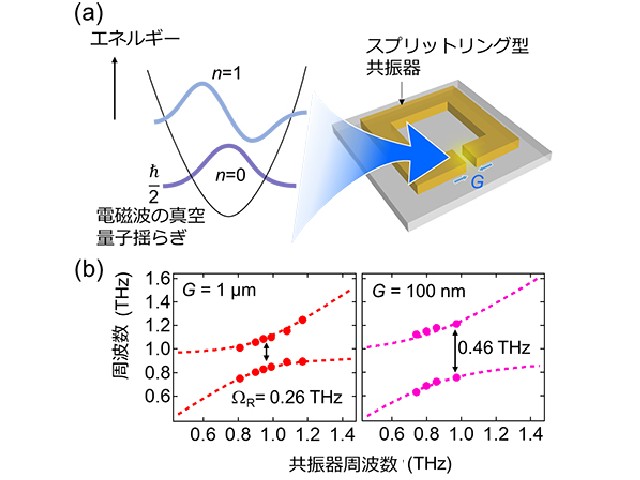
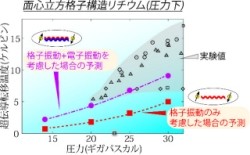
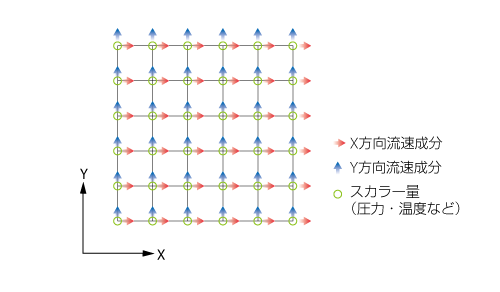
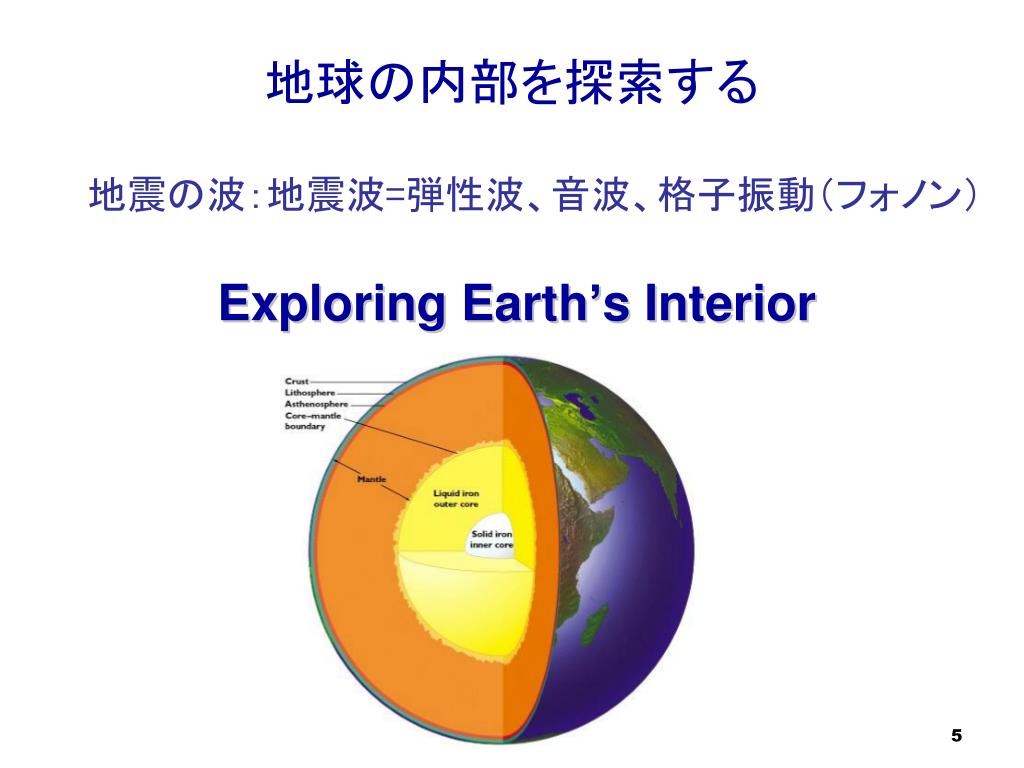
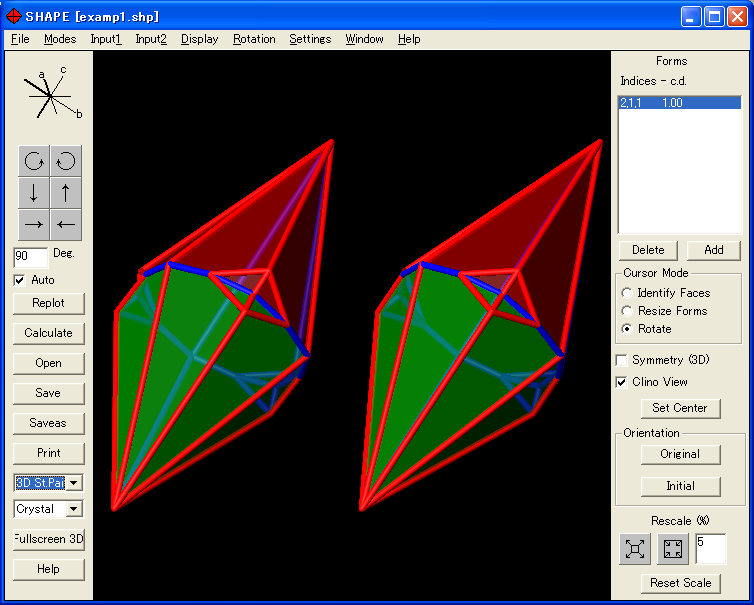
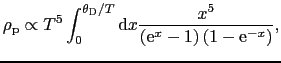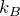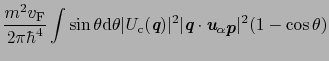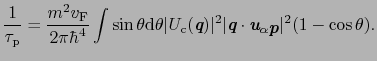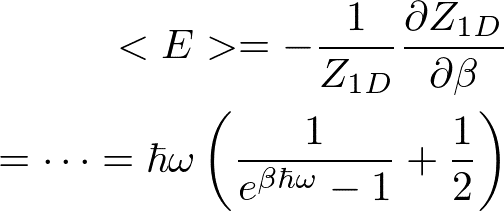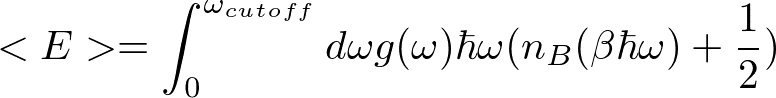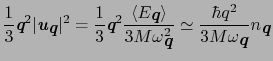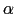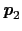Images of 格子振動
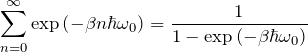
\begin{eqnarray*}\sum_{n=0}^{\infty} \exp{\left(-\beta n\hbar \omega_0\right) } = \frac{1}{1-\exp{\left(-\beta \hbar \omega_0\right) } }\end{eqnarray*}
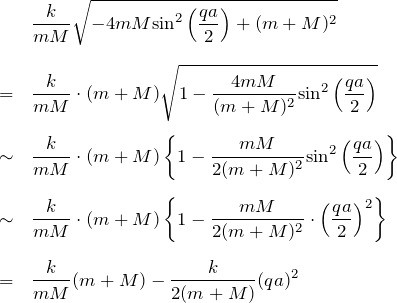
\begin{eqnarray*}&&\frac{k}{mM} \sqrt{-4mM{\rm sin}^2 \left(\frac{qa}{2}\right) + (m+M)^2}\\ \\&=&\frac{k}{mM}\cdot (m+M) \sqrt{1-\frac{4mM}{(m+M)^2} {\rm sin}^2 \left( \frac{qa}{2} \right)}\\ \\&\sim&\frac{k}{mM}\cdot (m+M) \left\{ 1-\frac{mM}{2(m+M)^2}{\rm sin}^2 \left(\frac{qa}{2}\right) \right\}\\ \\&\sim&\frac{k}{mM}\cdot (m+M) \left\{ 1-\frac{mM}{2(m+M)^2}\cdot\left(\frac{qa}{2}\right)^2 \right\}\\ \\&=&\frac{k}{mM}(m+M)-\frac{k}{2(m+M)}(qa)^2\end{eqnarray*}
![\begin{eqnarray*}3N_A\frac{d}{dT}\braket{\varepsilon}&=&3N_A\hbar \omega_0\frac{-\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\cdot \frac{d}{dT}\left( \frac{\hbar \omega_0}{k_B T}\right)\\ \\&=&3N_A \hbar \omega_0\frac{-\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\cdot \left( -\frac{\hbar \omega_0}{k_B T^2}\right)\\ \\&=&3N_A k_B\left( \frac{\hbar \omega_0}{k_B T}\right)^2\cdot\frac{\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\\ \\&=&3R\frac{\left( \frac{\hbar \omega_0}{k_B T}\right)^2\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2} \quad (\because R=N_A k_B)\end{eqnarray*}](https://batapara.com/wp-content/ql-cache/quicklatex.com-1d6f852bc302a9c4b0ed74dbf1f7f658_l3.png)
\begin{eqnarray*}3N_A\frac{d}{dT}\braket{\varepsilon}&=&3N_A\hbar \omega_0\frac{-\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\cdot \frac{d}{dT}\left( \frac{\hbar \omega_0}{k_B T}\right)\\ \\&=&3N_A \hbar \omega_0\frac{-\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\cdot \left( -\frac{\hbar \omega_0}{k_B T^2}\right)\\ \\&=&3N_A k_B\left( \frac{\hbar \omega_0}{k_B T}\right)^2\cdot\frac{\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2}\\ \\&=&3R\frac{\left( \frac{\hbar \omega_0}{k_B T}\right)^2\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}}{\left[\exp{\left(\frac{\hbar \omega_0}{k_B T} \right)}-1\right]^2} \quad (\because R=N_A k_B)\end{eqnarray*}


![固体物理 -格子振動・誘電体ー [ 作道 恒太郎 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/0522/9784785320522.jpg?_ex=300x300)