Images of 極値分布

極値をもつための条件 view page

エラスリス アコンカグア アルト カルメネール 2019年 エデュアルド チャドウィック チリ アコンカグア ヴァレーErrazuriz ACONCAGUA ALTO Carmenere 2019…view page

極値の求め方 view page

次数下げによる極値計算 view page

Rを使って極値理論をファイナンスへ応用してみた（その１）はじめに極値理論とは一般化極値分布パッケージBlock maxima モデル参考文献 view page

【全品半額coupon事前配布中】ピールオフ ベースジェル “ペロリン” ベースに塗ってジェルネイルをするだけで剥がせる！ オフ | ジェルネイル ベース はがせる クリアジェル ネイル…view page

2015LETシンポジウム 最大増加語数のモデリング view page

f:id:munemakun:20180909203952p:plain view page

極値の問題 view page

【全品半額coupon事前配布中】超高発色 マグネットネイル フルーツの果汁のような透明感あふれる 「FruitMagnet」 カラージェル ジェルネイル クリアカラー フルーツマグネット…view page

極値の問題 view page

極値（極大値・極小値）を持つ条件と持たない条件 view page

極値（極大値・極小値）を持つ条件と持たない条件 view page

OPI オーピーアイ ベースコート 15ml NTT10 国内正規品 O・P・I ベース・トップコート [0015/NTT10] メール便無料[A][TG100] ナチュラルネイル ベースコート…view page

f:id:hasegawa-yuta289:20200811225600p:plain view page

f:id:hasegawa-yuta289:20200811225126p:plain view page

極値を持つ(持たない)条件の判別式を用いた求め方とは？【他の応用問題アリ】 view page

【公式】ohora Gel Lamp：OHOL-02 ohora gelnails nail オホーラ ネイル ジェルネイル ネイルシール セルフネイル ネイルステッカー おうちネイル…view page

第一種極値分布 view page

極大値・極小値の意味と求め方 view page

【極大値・極小値】定義と求め方→最大値・最小値とは求め方が異なる！ view page

＼ポイント5倍12/19 20:00～12/26 01:59／＼楽天ランキング1位／【メール便OK】胡粉ネイル ベース＆トップコート 爪に優しく妊婦さんや子供も使える。ネイルアートに。速乾無添加…view page

【微分法】極大と極小の意味 view page

許容限界区間 (非正規分布)の分布の方法と計算式 view page

極方程式のグラフの求め方 view page

♪　＃01　【THREE】　スリー ネイルポリッシュトップコート　7mL　＃01 SILVER LINING＜ネイル/トップコート＞＜THREE Nail Polish Topcoat＞view page

くものパチスロ専業雑記 > view page

画像 view page

極値（極大値・極小値）を持つ条件と持たない条件 view page

【最大3％OFF】 【送料無料】 最新ネイル SNS ディップネイル シーラードライ Sealer Dry 15ml UVライト LEDライト不要 手に優しい 爪に優しい 長もち ネイル…view page

関数の極値 (導関数が不連続な場合) 次の関数はx=0において極値を持つかどうか、平均値の定理を利用 view page

異常気象リスクマップ view page

第一種極値分布 view page

ハローキティ ネイル 8本 香り付き 19899 ネイル はがせる マニキュア 水溶性 おもちゃ キッズコスメ キッズネイル おしゃれ カラフル 子供 こども キッズ かわいい 女の子…view page

第一種極値分布 view page

第一種極値分布 view page

【気象データ】「〇〇年に一度の大雨」の算出 (当てはめる分布関数の解説編)【統計解析】 view page

【12/30 当店ポイント10倍】エプロン ネイルガーデン Nail garden サロンワークエプロン(ネイビーリボン) ネイル関係雑貨…view page

極値 view page

極値分布とはなにか view page

関数が極値をもつ・もたない条件 view page

【送料無料(ゆうパケット)】BRO. FOR MEN Nail Coat クリア【メンズ 男性用 ネイルコート 爪 保護 ネイルケア】view page

極値統計学に軽く触れてみる view page

3次関数が極値をもつ条件 極値をもたない条件 view page

極値の求め方と判定条件：具体例と注意点 view page

NAIL DE DANCE ネイルデダンス　パウダー　001　コサックホワイト　20gview page

極値（極大値、極小値） view page

一般化極値分布 view page

フローサイトメトリー（FCM）の原理をできるだけ簡単に、わかりやすく解説！ view page

プリアンファ アームレスト［アイボリー/グレー/ブラック/クリーム］/ アームパッド 腕 腕置き ネイリスト ネイルサロン プロ PRO ネイル 業務用 プロ仕様 ネイルサロン ジェルネイル…view page

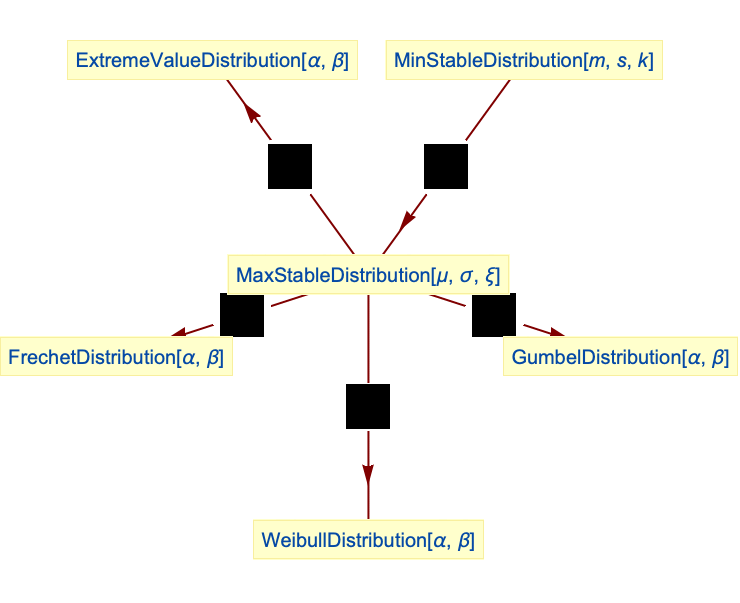
WOLFRAM MaxStableDistribution詳細予備知識例題関連項目関連するガイド履歴 view page

Ｎo.２　実用部材の疲労強度 　　　　　　　　　　に関する研究 鹿島　巌 酒井　徹. view page