Images of 正多胞体

f:id:Natsu1014_brog:20210222104729p:plain view page

正多胞体 高次元正多面体原論【電子書籍】[ H. S. M. コクセター ]view page

什么是合胞体？ view page

商品一覧 view page

多胞体¶ view page

正多胞体 高次元正多面体原論／H．S．M．コクセター／一松信／岡田好一【3000円以上送料無料】view page

1.2.3多细胞生物体的结构层次 view page

正多胞体 view page

十胞体 view page

正多胞体　高次元正多面体原論　H．S．M．コクセター/著　一松信/監訳　岡田好一/訳　日野雅之/訳　宮崎興二/訳view page

 牛呼吸合胞体病毒病(BRSV) view page

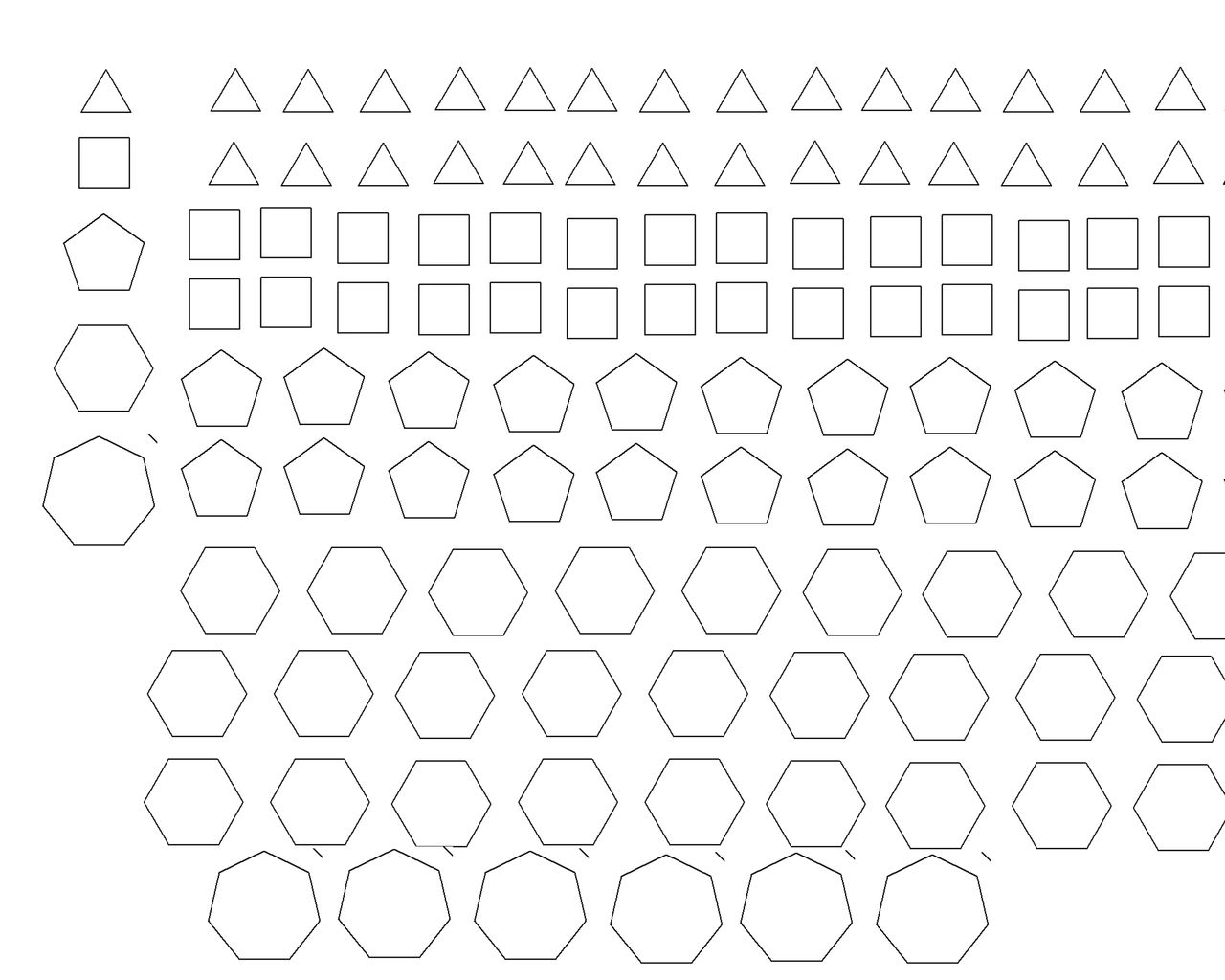
発想力教育研究所 素数誕生のメカニズム アルキメデス以来の新種発見！正七角形を使った半正多面体 コメント view page

Image Mission スタッフ日記 view page

正多胞体 高次元正多面体原論 / 原タイトル:REGULAR POLYTOPES 原著第3版の翻訳[本/雑誌] (数学クラシックス) / H.S.M.コクセター/著 一松信/監訳 岡田好一/訳…view page

四维均匀多胞体的列表(阿基米德类) view page

什么是合胞体？ view page

商品一覧 view page

正多胞体 高次元正多面体原論／H．S．M．コクセター／一松信／岡田好一【1000円以上送料無料】view page

常见的金属晶体结构类型有哪几种，绘出其晶胞图，说明其主要特征常见的金属晶体结构类型有哪几种，绘出其晶胞图，说明其主要特征 view page

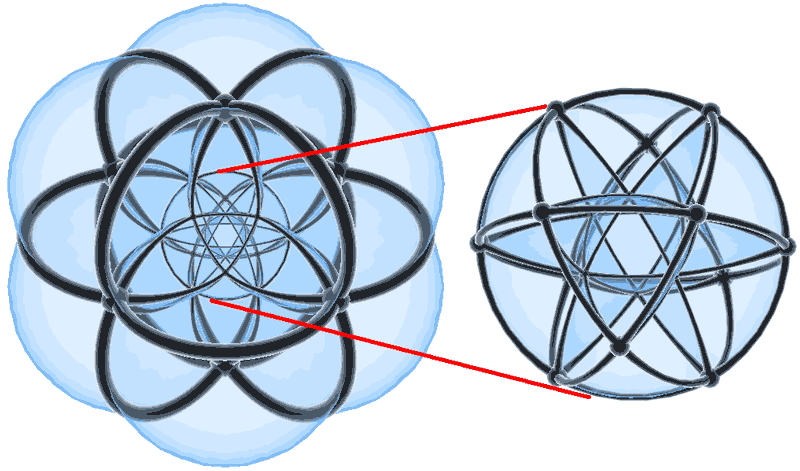
Blog de Hqak (WXYHLY) 四维空间（三）：谈正多胞体 view page

动物体的结构层次-人体的四大组织.ppt_第3页 view page

正多胞体 高次元正多面体原論view page

Yahoo!知恵袋ブラックホールは本当にあるのですか？ 高い重力のかかる場所はそうでない場所に比べ時間の進み方が遅くなるのなるんですよね？ view page

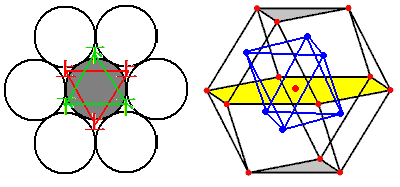
Blog de Hqak (WXYHLY) 四维空间（三）：谈正多胞体 view page

絵画の園 view page

正多胞体 高次元正多面体原論 数学クラシックス / 一松信 【全集・双書】view page

什么是合胞体？ view page

为什么24阶魔尺照着感觉就能扭出正方体 view page

抽象的な科学と技術イラスト。未来的な仮想サイバー空間の背景。3Dイラストのイラスト素材 view page

正多胞体 高次元正多面体原論view page

Yahoo!知恵袋正六面体と正八面体が、双対多面体の関係になることの、証明って、どうやればいいんですか？教えてください。 view page

画像 view page

第１７回　立体の展開図｜中学受験専門受験塾ドクターが「算数」の偏差値をアップさせる奥義を伝授！今後の目次ポイントが身につく問題実践講座①【ポイントNo.34】「面と面をつなぐ辺から頂点を考える」【正解①】ポイントが身につく問題実践講座②【正解②】開成・筑駒・灘の問題で今日のポイントを使う前回のチャレンジ問題の答え今日のポイントを使って問題にチャレンジ！ view page

【送料無料】正多胞体　高次元正多面体原論／H．S．M．コクセター／著　一松信／監訳　岡田好一／訳　日野雅之／訳　宮崎興二／訳view page

正八泡体の切断立体 view page

正八面体の展開図：ダウンロード無料のテンプレート倉庫 view page

正八面体 view page

正多胞体 高次元正多面体原論view page

正八面体に内接する球 view page

●この世界の真の姿は「非局所性」ーアンプリチューヘドロンー view page

四次元立方体（正八胞体）が三次元空間を通過する様子をmatplotlibで描画はじめに四次元立方体とは今回やること三次元の場合四次元の場合サンプルコード結果 view page

正多胞体　高次元正多面体原論view page

f:id:asangi_a4ac:20201204100755p:plain view page

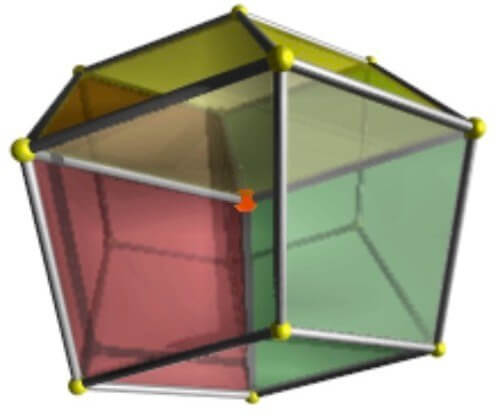
テセラクトとは？再現困難と言われている四次元の超立方体である正八胞体の世界観 view page

Cantitruncated 24-cellと双対多胞体(正八角形座標配置) view page

正多胞体 高次元正多面体原論view page

正十六胞体 view page

絵画の風 view page

作って遊ぼう&学校の応援 view page

Cantitruncated 24-cellと双対多胞体(正八角形座標配置) view page

商品一覧 view page