Images of 超幾何関数

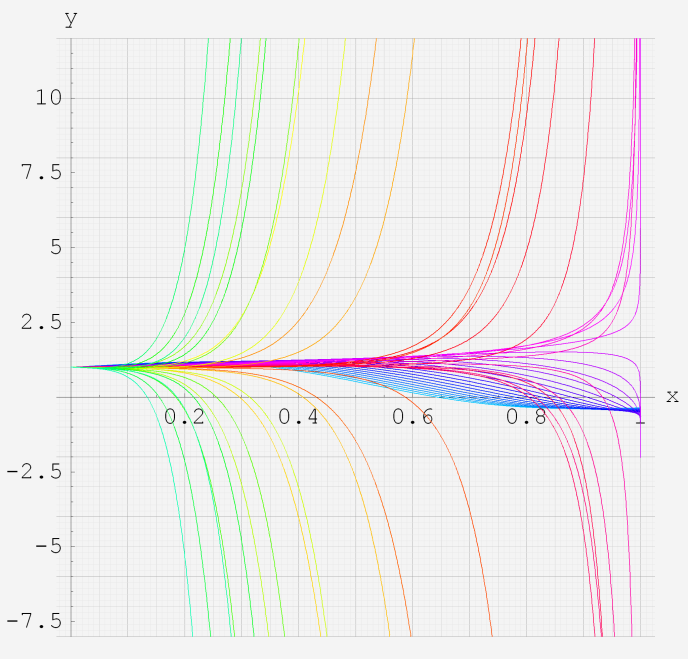
特殊関数 グラフィックスライブラリー Graphics Library of Special functions view page

私説　超幾何関数 対称領域による点配置空間の一意化 （共立講座　21世紀の数学　24） [ 吉田　正章 ]view page

下のソーシャルリンクからフォロー view page

無限級数の収束性１(コーシー、ダランベールなど) view page

f:id:tsujimotter:20200929175211p:plain:w400 view page

【中古】 私説　超幾何関数 対称領域による点配置空間の一意化 共立講座　21世紀の数学24／吉田正章(著者)view page

多項分布・負の二項分布・超幾何分布【統計検定準１級のための数学⑥】 view page

超幾何分布とは？　期待値と分散の導出、エクセル関数の使い方 view page

4F3の特殊値の計算例（一般化超幾何級数のEuler積分表示） view page

共立講座21世紀の数学　24　私説超幾何関数　対称領域による点配置空間の一意化　木村俊房/〔ほか〕編集view page

空蟬 view page

等比数列の和 view page

【中3数学】展開の公式のやり方は？問題を使って徹底解説！ view page

【中古】 超幾何関数論 (シュプリンガー現代数学シリーズ)view page

画像 view page

導来代数幾何入門 導来代数幾何入門 view page

代数幾何入門 ＜岩波オンデマンドブックス＞関連キーワード読後レビュー復刊投稿時のコメントおすすめ商品支払い / 配送方法 view page

【中古】超幾何関数論 (シュプリンガー現代数学シリーズ)view page

紀伊國屋書店 view page

紀伊國屋書店 view page

導来代数幾何入門導来代数幾何入門 view page

超幾何関数 (すうがくの風景 7)view page

代数幾何02 極大イデアルとは点である代数幾何02 極大イデアルとは点である view page

代数幾何学入門 中野茂男／著の商品画像｜ナビ view page

Jij Tech Blog 代数幾何の考え方　其の二 view page

超幾何関数 すうがくの風景 / 原岡喜重 【全集・双書】view page

※オイラーのφ関数だけ※(オイラーのφ関数の和) view page

1989　岡山大学MathJax view page

引き続き代数幾何を勉強するためのスレッド view page

【中古】超幾何関数論 (シュプリンガー現代数学シリーズ)view page

紀伊國屋書店 view page

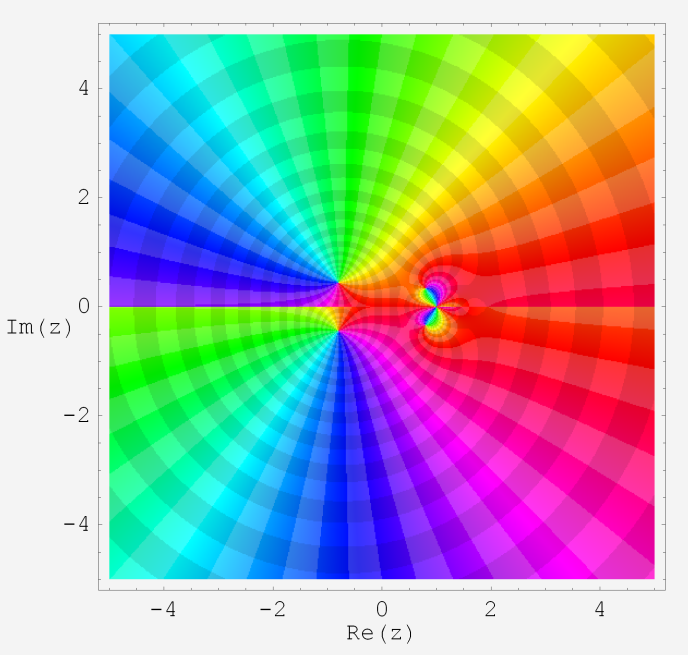
特殊関数 グラフィックスライブラリー Graphics Library of Special functions view page

紀伊國屋書店 view page

【中古】 超幾何関数論 (シュプリンガー現代数学シリーズ)view page

やさしく学べる線形代数 view page

代数幾何学 ＜現代数学レクチャーズ B-5＞ view page

中学数学「比例と反比例」の教え方①　関数とは何か？ view page

超幾何関数 (すうがくの風景 7)view page

nushio's diary このまえから代数幾何学になってる代数学 view page

古本と中古自転車の現代屋 view page

ますいしいのブログ2021年　兵庫県立大学・工　数学　第５問 view page

【中古】 超幾何関数論 (シュプリンガー現代数学シリーズ)view page

初学者のための代数幾何 view page

円周率の求め方（いろいろな計算式） view page

代数幾何学 view page

【中古】　共立講座　21世紀の数学　24　私説超幾何関数　吉田正章　【古本・古書】view page

profile-image view page

導来代数幾何入門 view page

f:id:medibook:20200910052722j:plain view page

【中古-非常に良い】 超幾何関数論 (シュプリンガー現代数学シリーズ)view page

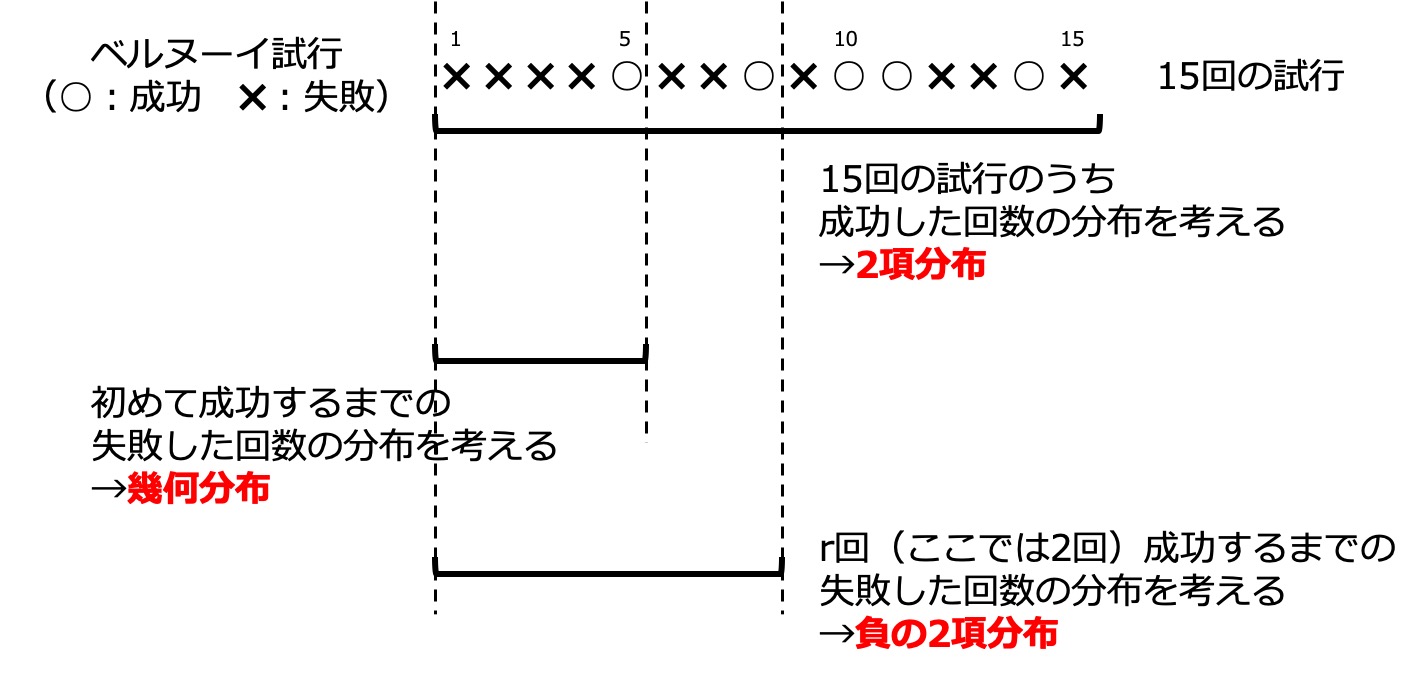
幾何分布は初めて成功するまでの失敗回数についての分布【無記憶性があります】 view page