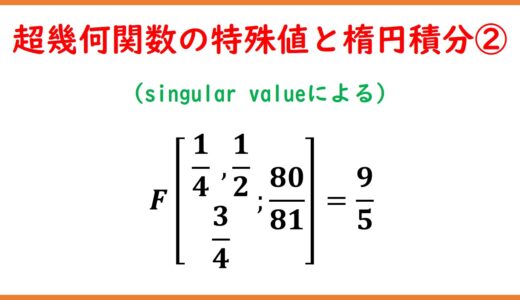
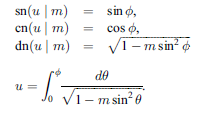20150922_楕円関数とおもしろい応用20150922_楕円関数とおもしろい応用

20150922_楕円関数とおもしろい応用20150922_楕円関数とおもしろい応用
![超楕円関数への招待 楕円関数の一般化とその応用【電子書籍】[ 松谷 茂樹 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/4292/2000015494292.jpg?_ex=300x300)
超楕円関数への招待 楕円関数の一般化とその応用【電子書籍】[ 松谷 茂樹 ]

20150922_楕円関数とおもしろい応用20150922_楕円関数とおもしろい応用

f:id:Shibaken_8128:20201210210951p:plain
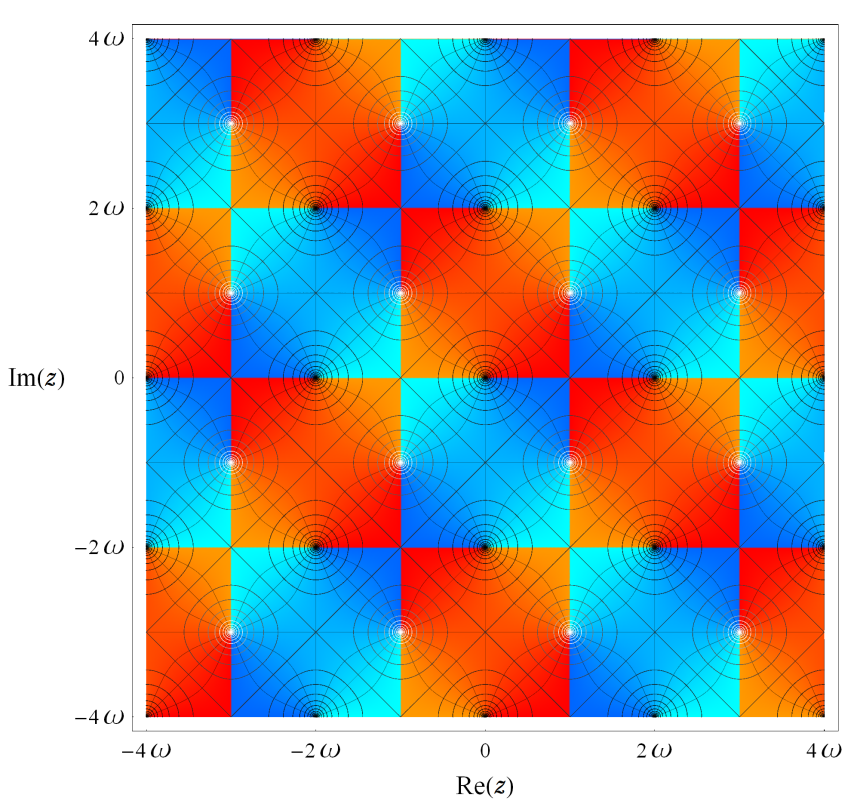
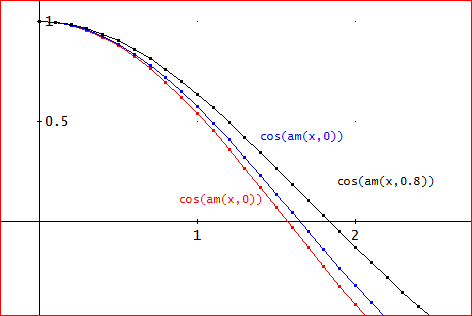
特殊関数 グラフィックスライブラリー Graphics Library of Special functions

20150922_楕円関数とおもしろい応用20170327_レムニスケートにまつわる色々な計算何もないところから数を作る何もないところから数を作る虚数は作れる!Swift で学ぶ複素数コードを書けば複素数がわかるパターン認識と機械学習 §6.2 カーネル関数の構成はじめてのパターン認識 第6章 後半パターン認識 05 ロジスティック回帰prml4.1.3-4.1.4Crfと素性テンプレートディジタル信号処理 課題解説 その4PRML 10.4 - 10.6スペクトラル・クラスタリング線形計画法入門ディジタル信号処理の課題解説 その3第4回MachineLearningのための数学塾資料(浅川)ディジタル信号処理の課題解説TokyoNLP#7 きれいなジャイアンのカカカカ☆カーネル法入門-C++Prml 4.1.1Nonparametric Factor Analysis with Beta Process Priors の式解説20150922_楕円関数とおもしろい応用
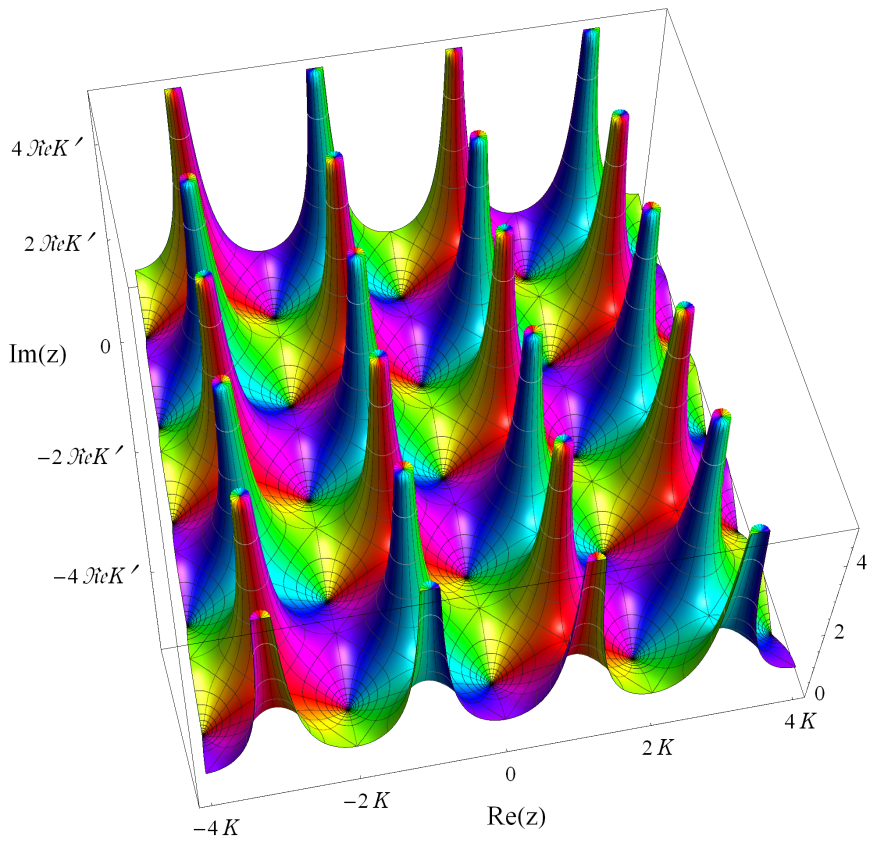
特殊関数 グラフィックスライブラリー Graphics Library of Special functions

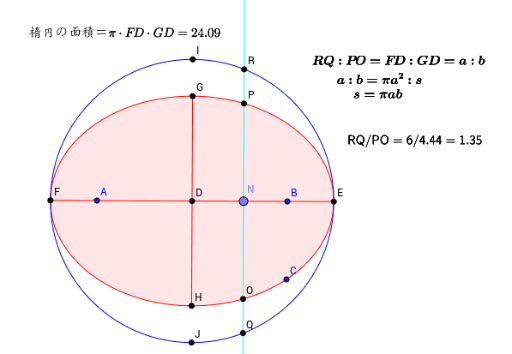
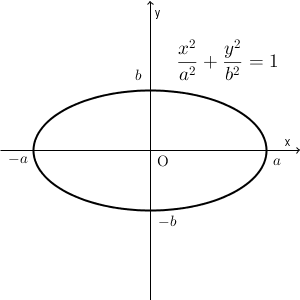
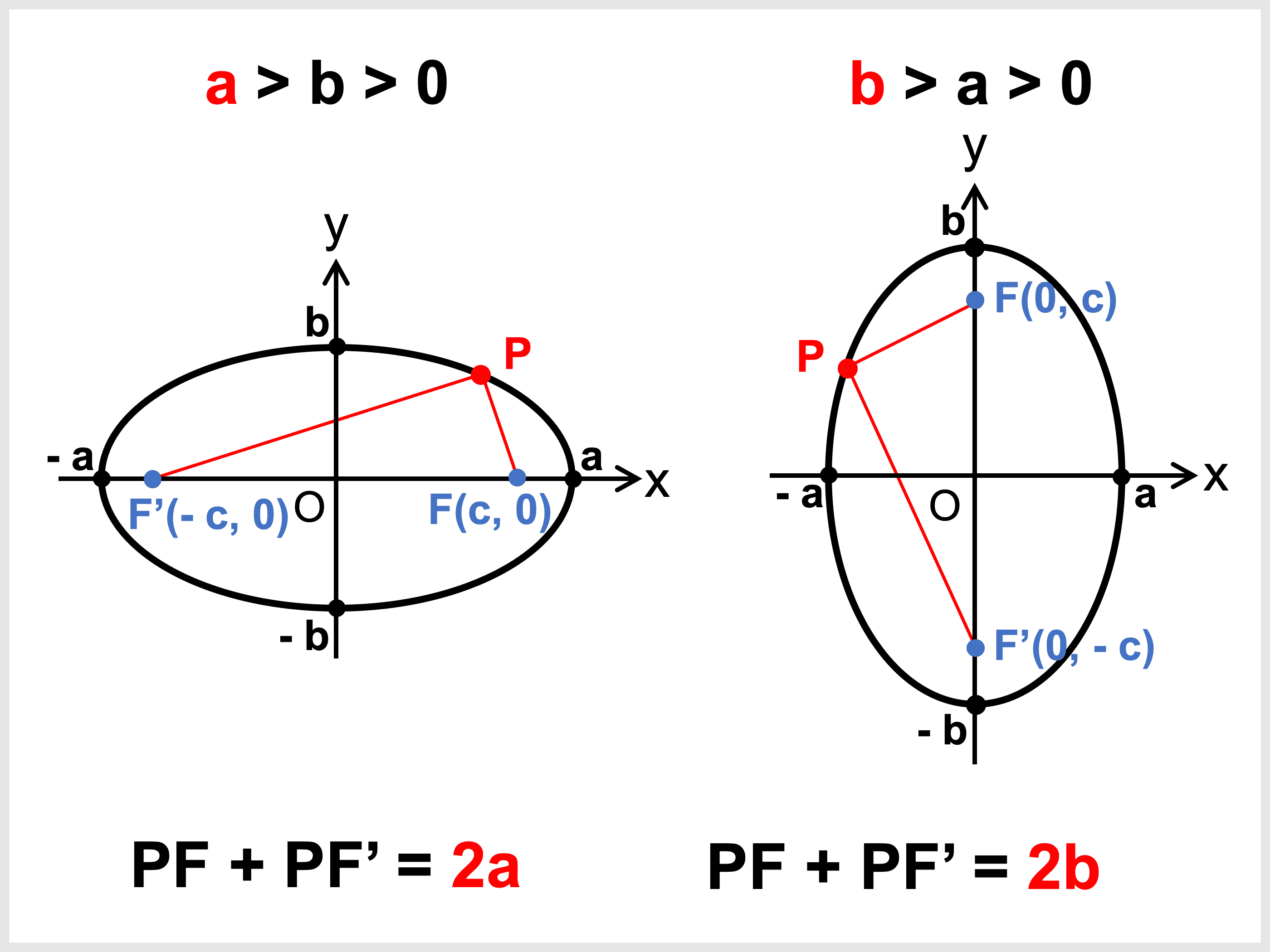
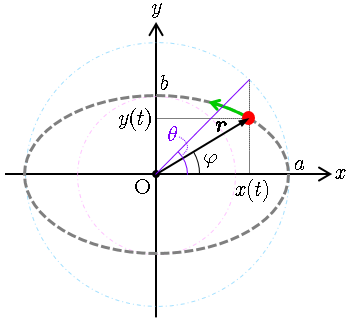
楕円の方程式・面積をマスターしよう!定期テスト1週間前からでも楕円をマスター

f:id:pianofisica:20190109170808p:plain
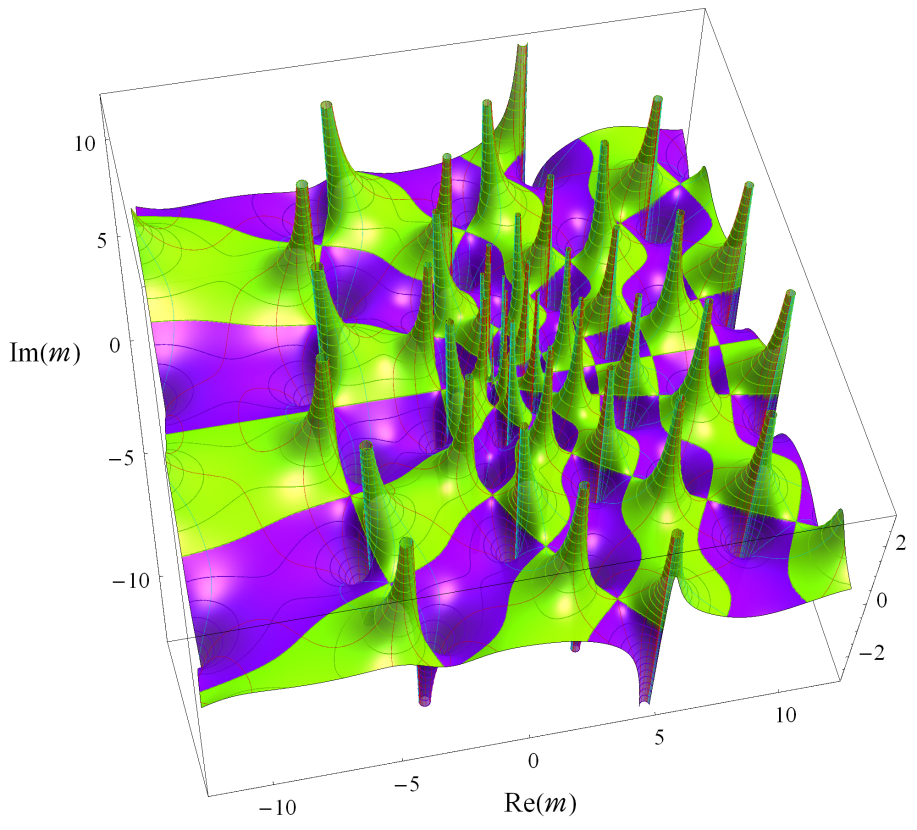
特殊関数 グラフィックスライブラリー Graphics Library of Special functions

特殊関数 グラフィックスライブラリー Graphics Library of Special functions

特殊関数 グラフィックスライブラリー Graphics Library of Special functions

特殊関数 グラフィックスライブラリー Graphics Library of Special functions

特殊関数 グラフィックスライブラリー Graphics Library of Special functions




![超楕円関数への招待 楕円関数の一般化とその応用 [ 松谷 茂樹 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/7003/9784764907003_1_3.jpg?_ex=300x300)


![超楕円関数への招待 楕円関数の一般化とその応用【電子書籍】[ 松谷 茂樹 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/4292/2000015494292.jpg?_ex=300x300)