Images of 絶対少年

ニコニコ動画 view page

【衝撃セール中 6/27 9:59迄】扇風機 dcモーター 左右自動首振り リビング扇風機 フルリモコン 静音 省エネ 風量9段階 YLX-DJD30E dc扇風機 リビングファン 羽根径30cm…view page

JavaScript is not available. view page

JavaScript is not available. view page

絶対少年 2005 絶対少年 2005 view page

『時間限定2000円クーポン』UNISEKA正規品 ネッククーラー 首掛け扇風機 ネックファン扇風機 携帯扇風機 通勤 熱中症対策 屋外作業 静音 羽なし 軽量 100段階 スポーツ 2025…view page

富山県高岡市福岡町で活動する福岡町柔道スポーツ少年団の指導者のブログ第544回 view page

絶対少年#26_1 view page

絶対少年 (1) [DVD] view page

クーポンで1,780円【楽天1位★テレビ紹介】 ハンディファン 冷却プレート 携帯扇風機 5000mAh 3200mAh クーラー 冷却プレート 強風 冷却モード 扇風機 卓上 小型扇風機…view page

AK-GARDEN　2010　絶対少年&フライングメガロポリス　新井恵子　グラスアクセサリーオブジェ　その１ view page

紀伊國屋書店 view page

メルカリ レア 鈴木真仁 Cdアルバム 絶対少年 邦楽 3 3 中古や未使用のフリマ view page

楽天1位 1秒冷却【COUPONで2,780円・超お得SALE】 ハンディファン 冷却プレート 携帯扇風機 -25℃冷却 100段階風量 高速暴風 ハンディ扇風機 首掛け 冷却プレート 扇風機…view page

AK-GARDEN　2010　絶対少年&フライングメガロポリス　絶対少年　（&Seyakku)　ブース　その２ view page

【新着】絶対少年 view page

絶対少年（全26話） view page

楽天1位！■爆売れ正規品■限定CPで3930円♪【2025年夏冷感・ファン＆1台2役】首掛け扇風機 冷却プレート 瞬間冷却 ネックファン ネッククーラー ★3段階風量×3段階冷感★ 羽根なし…view page

絶対少年（全26話） view page

絶対少年（全26話） view page

絶対少年（全26話） view page

【2025改良進化版★クーポンで最安1,937円】ハンディファン 冷却プレート 2025 大風量 100段階強力冷風 PROMAX 超軽量 瞬間冷却 卓上扇風機 ハンディ扇風機 手持ち扇風機…view page

絶対少年第13話 谷川希紗と見慣れぬ存在 view page

“たわわな水着姿に”『週チャン』に絶対的美少女まるぴが再登場！ culture230126-w-champion-04 view page

Amazon Raitaのfgo落書き本 絶対少女 Fate Grand Order 魔法少女 アニメ 萌えグッズ 通販 view page

リズム 公式 | ハンディファン 2025 大風量 静音 3Way ( 手持ち 首かけ 卓上 ) 風量5段階 Type-C対応 カラビナ＆ストラップ付き 小型 かわいい 携帯扇風機 卓上扇風機…view page

【魔法少女】1/6『倉本エリカ（くらもと えりか）ビーチバレーver.』コンパチブル美少女フィギュア【ロケットボーイ】より2023年8月発売予定☆ view page

『新・絶対的美少女、お貸しします。 57 園田みおん 【MGSだけの特典映像付】 +15分』美少女|・･･/絶対的鉄板シチュエーション 6 瀬名きらり 【MGSだけの特典映像付】 +25分他 view page

DISCOGRAPHY view page

【10P・クーポンで最安2199円】「楽天1位」「-28℃瞬間冷却＆手持ち冷蔵庫」扇風機 ハンディファン ハンディ扇風機 冷却プレート 首掛け 冷却 暴風 手持ち扇風機 1台4役 100段階…view page

絶対少女 (RAITA) Volshebnik-1640 view page

男性向一般同人誌　<<オリジナル>> 絶対純白・魔法少女 / RAITA / Absolute Girl(絶対少女) view page

サークル：絶対少女帝国 同人誌・同人グッズ一覧 view page

＼6/22まで★20％OFFクーポン→1,904円！／ハンディファン 冷却プレート 携帯扇風機 最大12時間稼働 小型扇風機 usb ハンディ扇風機 6段階モード ハンディーファン 軽量 強力…view page

同人音楽CDソフト　Starry Night / 絶対少女領域 view page

術後アンスラサイクリン+タキサン vs TCに終止符 view page

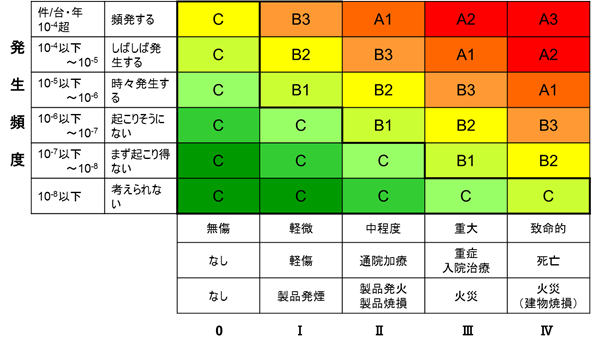
医療機器企業におけるリスクマネジメントについて研究するページ1.    R-Map手法とは　ISO/IEC Guide 51の定義では、リスクとは「危害の発生の確率とそれが発生したときの重大性の組合せ」で ある。 　実際に確率を正確に見積もるのは容易なことではない。白鳥は白いものという思い込みがあったのに、オ ーストラリアで黒い白鳥が発見されたことにちなみ、確率で予測できないことを「ブラックスワン」と呼 ぶ。 　未曽有の巨大地震とその後の原発事故もブラックスワンの一種といえる。確率は極めて小さいが、ゼロで はない破滅的リスクも人間の嫌う曖昧さに通じているかもしれない。 　このような時、リスクの発生前後を比較すると、人間は往々にして完全な無視から過剰な反応へと正反対 に振れる。米国の法学者、キャス・サンスティーンは、どちらの極端な態度にも陥らず、費用対効果を考慮 しながら、予防的なリスク削減措置を講じるべきだと主張している。 　製品や設備、環境などの状況から、起こりうる危害の程度と発生頻度を推定し、危険の大きさを評価する リスクアセスメントの手法の1つにR-Map手法というものがある。R-Map手法には、リスクを定量評価し、 社会的に許容されるか否かを視覚的に判断しやすいという特徴がある。 　2008年に経済産業省は「電気用品安全法」や「消費生活用製品安全法」などのいわゆる製品安全4法を改 正し、開発設計段階でのリスクアセスメントの実施を義務付ける方針を表明した。同省は、R-Mapの導入を 想定している。 　　　　　　 2.    R-Map手法によるリスク評価 　R‐Map法では、リスク評価をA3、A2、A1、B3、B2、B1、Cというように割り振る。（図2） リスクの大きさを、受け入れられないリスク「A」、原則は許容されないがコストや効用によって認める 「B」、許容可能な「C」の3つに大別し、AやBのリスクが、Cになるまで対策と評価を繰り返すのである。 　　　3.    航空機はなぜ飛行が許されるのか　航空機の墜落事故においては、その重大性は甚大である。ひとたび事故が発生すれば、その被害は計り知れないものとなるだろう。それでは、なぜ航空機は飛行が許され、また乗客も安心して利用しているのであろうか。 　米国の国家運輸安全委員会（NTSB）の行った調査によると、航空機に乗って死亡事故に遭遇する確率は 0.0009%であるという。米国国内の航空会社だけを対象とした調査ではさらに低く0.000034%となる。 　これは8,200年間、毎日無作為に選んだ航空機に乗って一度事故に遭うか遭わないかという確率である。 これが「航空機は最も安全な交通手段」という説の根拠となっている。 　ちなみに米国国内において自動車に乗って死亡事故に遭遇する確率は0.03%なので、その33分の1以下の 確率ということになる。 　つまり、航空機事故の発生確率が極めて低いのである。R‐Map法では一番右の下『C』に相当する。発生 した場合は致命的であるが、発生がほぼ考えられない。発生頻度と重大性を掛け合わせた数値は非常に低い ということである。これによって、航空機は飛行することが可能なのである。 　ちなみに、2001年9月の米国同時多発テロ事件の後、米国人の多くが民間航空機による移動を避けて自家 用車による移動を選択したために、同年の10月から12月までの米国における自動車事故による死者の数は 前年比で約1,000人増加したという。なんとも皮肉な結果となってしまった。 4.    危害の程度　危害の程度では、一般的に定性的な表現と定量的表現が用いられる。（図3） 　当然のことながら、規制当局の期待は定量的な表現だ。ただし、製薬業界、医療機器業界では、どうして も定量的に評価することは困難である場合が多い。 　定性的評価の表現とは、『致命的（Catastrophic）』『重大（Critical）』『中程度（Marginal）』『軽微 （Negligible）』『無傷（None）』などである。多くの場合、定性的な表現で評価をしがちになる。 　一方、定量的な表現は、人に対する危害が『死亡』『重傷・入院治療を要する』『通院加療が必要』『軽傷』 『なし』などである。このように具体的な危害を推定することが望ましい。例えば、医薬品に不純物が混じ ってしまった場合、具体的に患者にどのような危害が生じるかを評価する。 5.    発生頻度 　発生頻度は、一番確率の高いものをレベルで5とする。発生頻度においても危害の程度と同様に、定性的 な表現と定量的表現が用いられる。（図4） 　 6.    発生頻度の確率的表現 　発生頻度の確率的表現では、10万台の製品が１年間稼働している中で、週に2回から1ヶ月に1回起きる 確率というのが『発生頻度5』のレベルである。月に1度から１年に1度というのが『発生頻度4』。10年に 1度というのが『発生頻度3』というように具体的な発生頻度を確率的に表現することもできる。（図5参照） view page

【テレビ紹介】楽天1位☆シシベラ ハンディファン 冷却プレート 冷却ハンディファン 扇風機 ハンディ cicibella 首かけ 扇風機 ミニ扇風機 バッテリー 扇風機 卓上 ハンディファン…view page

診断・リスク評価　治療 view page

f:id:medibook:20200701050918j:plain view page

知っておきたい投資信託のこと view page

＼11%OFF★2,999円／扇風機 リビング テクノス メカ式 扇風機 扇風機 タイマー タイマー付き 首振り 静か 静音 テクノス クール用品 リビングファン メカ式 首振り 夏 季節家電…view page

TCFD提言に基づく情報開示 view page

温暖化で死亡リスクは減少する view page

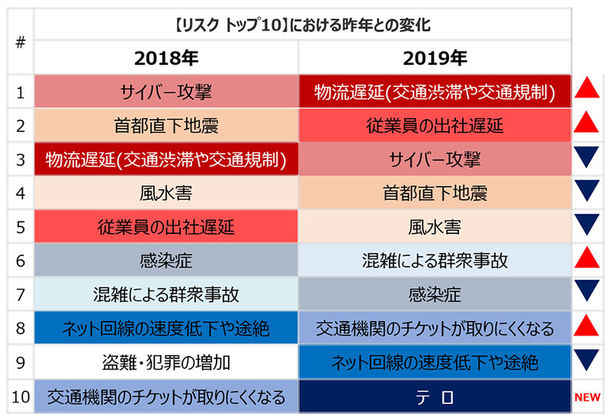
東京オリンピック、物流遅延や出社に危機感。発生可能性の高いリスクへの危機感が高まる view page

Francfranc 2025年モデル フレ ハンディファン ウェーブ 携帯・手持ち扇風機 フランフラン インテリア・生活雑貨 扇風機・空気清浄機・加湿器 シルバー ブルー【送料無料】view page

絶対絶望少女　ダンガンロンパ　Another　Episode　(1) 絶対絶望少女　ダンガンロンパ　Another　Episode　(1) view page

『絶対絶望少女 ダンガンロンパ Another Episode』店舗別予約特典が一挙公開！ view page

ダンガンロンパ 絶対絶望少女 デコダマ view page

[P5倍 6/22 12時〜] [先着500名限定/1000円クーポン配布中] 360°首振り サーキュレーター 扇風機 DCモーター リモコン付き 省エネ DCファン 360度首振り 熱中症対策…view page